资源简介

2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线 5.2平行线及其判定 课后练习
一、选择题
1．下列说法中，正确的是（　　）
A．过一点有无数条直线与已知直线平行 B．同位角相等
C．相等的角是对顶角 D．平行于同一条直线的两条直线平行
2．下列说法中，正确的是（　　）
A．两点之间的距离是两点间的线段 B．与同一条直线垂直的两条直线也垂直
C．同一平面内，过一点有且只有一条直线与已知直线垂直 D．同旁内角互补
3．给出下列说法：①过两点有且只有一条直线；②连接两点的线段叫作两点间的距离；③两点之间，线段最短；④若，则点B是线段AC的中点；⑤同一平面内过一点有且只有一条直线与已知直线垂直；⑥平行于同一直线的两条直线互相平行．其中正确的个数是（ ）
A．2 B．3 C．4 D．5
4．下列命题中是真命题的有（ ）
①两个角的和等于平角时，这两个角互为邻补角；②过一点有且只有一条直线与已知直线平行；③两条平行线被第三条直线所截，所得的一对内错角的角平分线互相平行；④图形B由图形A平移得到，则图形B与图形A中的对应点所连线段平行（或在同一条直线上）且相等；⑤因为＝5，所以＝a．
A．2 个 B．3 个 C．4 个 D．5 个
5．下列命题中，正确的是（ ）．
①若，则；②同位角相等，两直线平行；③相等的角是对顶角；④经过直线外一点，有且只有一条直线与这条直线平行．
A．①②③④ B．②④ C．①②④ D．②③④
6．如图，在下列给出的条件中，可以判定的有（ ）
①；②；③；④；⑤．
A．①②③ B．①②④ C．①④⑤ D．②③⑤
7．如图，点E在的延长线上，则下列条件中，不能判定的是（ ）
A． B． C． D．
8．如图，用直尺和三角尺画图：已知点P和直线a，经过点P作直线b，使，其画法的依据是（ ）
A．过直线外一点有且只有一条直线与已知直线平行 B．两直线平行，同位角相等
C．同位角相等，两直线平行 D．内错角相等，两直线平行
9．如图，直线被直线所截，下列条件中不能判定a//b的是（ ）
A． B． C． D．
10．如图，给出下列条件：①∠1＝∠2：②∠3＝∠4：③AB∥CE，且∠ADC＝∠B：④AB∥CE，且∠BCD＝∠BAD．其中能推出BC∥AD的条件为（　　）
A．①② B．②④ C．②③ D．②③④
二、填空题
11．下列说法中正确的有 __________ ．（填写序号）
①两条直线被第三条直线所截，同位角相等；
②在同一平面内，两条直线的位置关系只有相交、平行两种；
③在同一平面内，过直线外一点有且只有一条直线与已知直线垂直；
12．下列说法：①对顶角相等；②两点间线段是两点间距离；③过一点有且只有一条直线与已知直线平行；④过一点有且只有一条直线与已知直线垂直；⑤若，则点C是线段的中点；⑥同角的余角相等正确的有_________．（填序号）
13．空间两直线的位置关系有___________________________．
14．如图，下列能判定的条件有_______个．
①；②；③；④．
15．如图，下列条件：①∠1＝∠2；②∠BAD+∠ADC＝180°；③∠ABC＝∠ADC；④∠3＝∠4；其中能判定AB∥CD的是_____（填序号）．
三、解答题
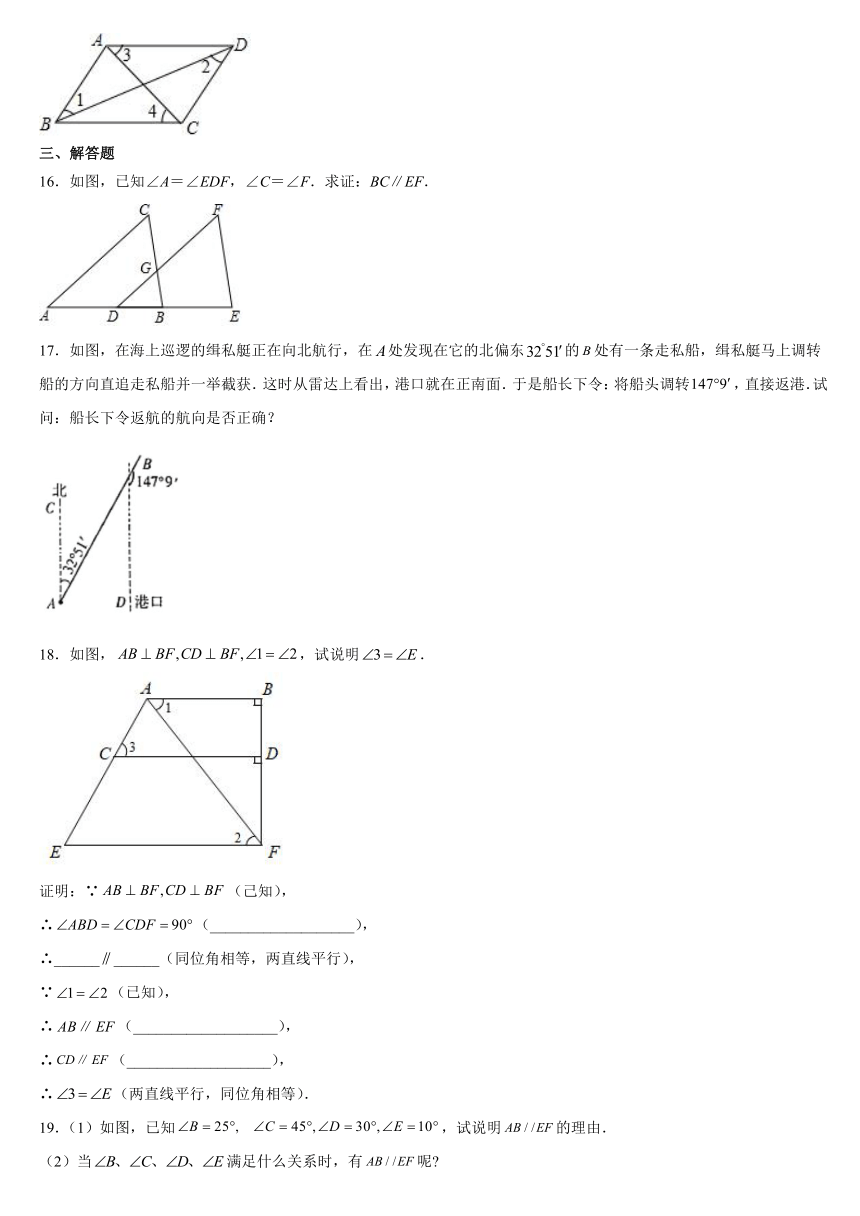
16．如图，已知∠A＝∠EDF，∠C＝∠F．求证：BC∥EF．
17．如图，在海上巡逻的缉私艇正在向北航行，在处发现在它的北偏东的处有一条走私船，缉私艇马上调转船的方向直追走私船并一举截获．这时从雷达上看出，港口就在正南面．于是船长下令：将船头调转，直接返港．试问：船长下令返航的航向是否正确？
18．如图，，试说明．
证明：∵（己知），
∴（___________________），
∴____________（同位角相等，两直线平行），
∵（已知），
∴（___________________），
∴（___________________），
∴（两直线平行，同位角相等）．
19．（1）如图，已知，试说明的理由．
（2）当满足什么关系时，有呢
20．如图，，平分，平分，．
（1）求证：；
（2）与平行吗？请说明理由．
21．一副三角板按如图所示叠放在一起，其中点B、D重合，若固定三角形AOB，改变三角板ACD的位置（其中A点位置始终不变）．
（1）当∠BAD＝　　°，CDAB．
（2）当∠BAD＝　　°，则三角板ACD有一条边与直角边OB平行．（写出所有可能情况）
22．如图，在6×6的正方形网格中，每个小正方形的边长是1，点M、N、P、Q均为格点（格点是指每个小正方形的顶点），线段MN经过点P．
（1）过点P画线段AB，使得线段AB满足以下两个条件：①AB⊥MN；②；
（2）过点Q画MN的平行线CD，CD与AB相交于点E；
（3）若格点F使得△PFM的面积等于4，则这样的点F共有 个．
23．如图，在8×6的正方形网格中，每个小正方形的顶点称为格点，点D是∠ABC的边BC上的一点，点M是∠ABC内部的一点，点A、B、C、D、M均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，并回答问题：
（1）过点M画BC的平行线MN交AB于点N；
（2）过点D画BC的垂线DE，交AB于点E；
（3）点E到直线BC的距离是线段 　 　的长度．
【参考答案】
1．D 2．C 3．C 4．A 5．B 6．D 7．B 8．C 9．D 10．D
11．②③
12．①④⑥
13．平行、相交、异面
14．1
15．①②．
16．证明：∵∠A＝∠EDF（已知），
∴AC∥DE（同位角相等，两直线平行），
∴∠C＝∠CGF（两直线平行，内错角相等）．
又∵∠C＝∠F（已知），
∴∠CGF＝∠F（等量代换），
∴BC∥EF（内错角相等，两直线平行）．
17．解：正确．
∵，
∴
∴
∵是正北方向
∴是正南方向．
∴船长下令返航的航向是正确的．
18．证明：∵（己知），
∴（垂直定义），
∴ABCD（同位角相等，两直线平行），
∵（已知），
∴（内错角相等，两直线平行），
∴（平行于同一条直线的两条直线平行），
∴（两直线平行，同位角相等）．
故答案为：垂直定义；AB；CD；内错角相等，两直线平行；平行于同一条直线的两条直线平行
19．解：（1）过点C作，过点D作，
，
；
（2）过点C作，过点D作，
若，则，
．
20．（1）证明：∵BE平分，平分,
∴，，
∵∠ABC＝∠ADC ，
∴∠2＝∠CDF，
∵∠1＝∠2 ，
∴∠1＝∠CDF，，
∴AB∥CD；
（2）AD∥BC，理由如下：
∵AB∥CD，
∴，
∵∠ABC＝∠ADC ，
∴∠ADC＋∠C＝180°，
∴AD∥BC，．
21．解：（1）如图所示：当CD∥AB时，∠BAD＝∠D＝30°；
如图所示，当AB∥CD时，∠C＝∠BAC＝60°，
∴∠BAD＝60°+90°＝150°；
故答案为：150或30；
（2）如图所示，当CD∥OB时，∠BAD＝45°﹣30°＝15°；
如图所示，当AD∥BO时，∠BAD＝∠B＝45°；
如图所示，当AC∥BO时，∠BAD＝45°+90°＝135°；
如图所示，当CD∥BO时，∠BAD＝180°﹣60°+45°＝165°；
如图所示，当AD∥BO时，∠BAD＝45°+90°＝135°；
如图所示，当AC∥BO时，∠BAD＝45°．
综上所述，∠BAD的度数为15°或45°或135°或165°．
故答案为：15或45或135或165．
22．（1）解：作图如下：
（2）
解：作图见（1）
（3）
如图：
故符合题意的点F有6个.
故答案为：6
23．解：（1）如图所示，点N即为所求；
（2）如图所示，点E即为所求；
（3）由题意可知：点E到直线BC的距离是线段DE的长度，
故答案为：DE．

展开更多......

收起↑