资源简介

中小学教育资源及组卷应用平台
2021-2022学年下学期武汉初中数学七年级期中典型试卷2
一．选择题（共10小题）
1．（2021春 洪山区期中）下列实数，，3.14159，﹣，，0.3030030003中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
2．（2021春 兴国县期末）下列图案是由图中所示的图案通过平移后得到的是（　　）
A． B． C． D．
3．（2012秋 南岸区期末）点P（3，﹣4），则点P在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．（2021春 虎林市期末）下列说法不正确的是（　　）
A．的平方根是
B．﹣9是81的一个平方根
C．0.2的算术平方根是0.04
D．﹣27的立方根是﹣3
5．（2021春 江岸区期中）如图，∠1＝∠2，∠3＝112°，则∠4等于（　　）
A．62° B．68° C．78° D．112°
6．（2021春 江岸区期中）一个正方形的面积扩大为原来9倍，它的周长变为原来的（　　）倍．
A．2 B．3 C．9 D．12
7．（2021秋 临渭区期中）已知A点的坐标为（3，a+3），B点的坐标为（a，a﹣4），AB∥y轴，则线段AB的长为（　　）
A．5 B．6 C．7 D．13
8．（2021春 青山区期中）下列命题中，真命题的个数有（　　）
①无限小数是无理数；
②立方根等于它本身的数有两个，是0和1；
③同位角相等；
④过一点有且只有一条直线与已知直线平行．
A．0个 B．1个 C．2个 D．3个
9．（2021春 红谷滩区校级期中）已知≈0.5981，≈1.289，≈2.776，则≈（　　）
A．27.76 B．12.89 C．59.81 D．5.981
10．（2021春 武昌区期中）如图，一个蒲公英种子从平面直角坐标系的原点O出发，向正东走3米到达点A1，再向正北方向走6米到达点A2，再向正西方向走9米到达点A3，再向正南方向走12米到达点A4，再向正东方向走15米到达点A5，以此规律走下去，当种子到达点A10时，它在坐标系中坐标为（　　）
A．（﹣12，﹣12） B．（15，18） C．（15，﹣12） D．（﹣15，18）
二．填空题（共6小题）
11．（2021春 洪山区期中）若a3＝8，＝2，则a+b＝　 　．
12．（2020秋 宝安区期末）实数a、b在数轴上所对应的点如图所示，则|﹣b|+|a+|+的值　 　．
13．（2002 泸州）如图，某宾馆在重新装修后，准备在大厅的楼梯上铺上某种红色地毯，已知这种地毯每平方米售价30元，主楼梯道宽2米，其侧面如图所示，则购买地毯至少需要　 　元．
14．（2021春 新洲区期中）把一张长方形纸片ABCD沿EF折叠后ED与BC的交点G，D、C分别在M、N的位置上，若∠EFG＝55°，则∠2﹣∠1＝　 　．
15．（2021春 滨江区校级期末）如图a，已知长方形纸带ABCD，将纸带沿EF折叠后，点C、D分别落在H、G的位置，再沿BC折叠成图b，若∠DEF＝72°，则∠GMN＝　 　°．
16．（2021春 江岸区期中）平面直角坐标系中，点M（x，y），N（x﹣2ky，y﹣3kx），MN＝7OM，当点M在y轴正半轴上时，k＝　 　．
三．解答题（共8小题）
17．（2021春 青山区期中）计算：
（1）|﹣|+2；
（2）﹣（）2﹣﹣．
18．（2021春 青山区期中）如图，直线AB，CD相交于点O，OE把∠BOD分成两部分．
（1）直接写出图中∠AOD的对顶角为　 　，∠DOE的邻补角为　 　．
（2）若∠AOC＝90°，且∠BOE：∠EOD＝2：3．求∠EOC的度数．
19．（2021春 武昌区期中）完成下面的推理填空：
如图，已知AB∥CD，∠1＝∠2，∠3＝∠4，求证：∠D＝∠DCE．
证明：∵AB∥CD，
∴∠2＝∠BAE（ 　 　）．
∵∠BAE＝∠3+　 　，
∴∠2＝∠3+　 　，
∵∠3＝∠4，
∴∠2＝∠CAD，
又∵∠2＝　 　，
∴∠CAD＝　 　，
∴AD∥　 　（ 　 　）．
∴∠D＝∠DCE．（ 　 　）．
20．（2021春 武昌区期中）平面直角坐标系中，将点A、B先向下平移3个单位长度，再向右平移2个单位后，分别得到点A′（3，﹣2）、B′（2，﹣4）．
（1）点A坐标为 　 　，点B坐标为 　 　，并在图中标出点A、B；
（2）若点C的坐标为（2，﹣2），求△ABC的面积；
（3）在（2）的条件下，如图所示网格中，点E为图中格点（不与C重合），且使得△ABE与△ABC的面积相等，符合条件的E点有 　 　个．
21．（2021春 洪山区期中）在正方形网格中，每个小正方形的边长均为1个单位长度，我们将小正方形的顶点叫做格点，如图，△ABC的三个顶点均在格点上．仅用一把无刻度直尺在给定的网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：
（1）将△ABC先向右平移5个单位长度，再向上平移3个单位长度，得到对应的△A1B1C1，画出平移后的△A1B1C1；
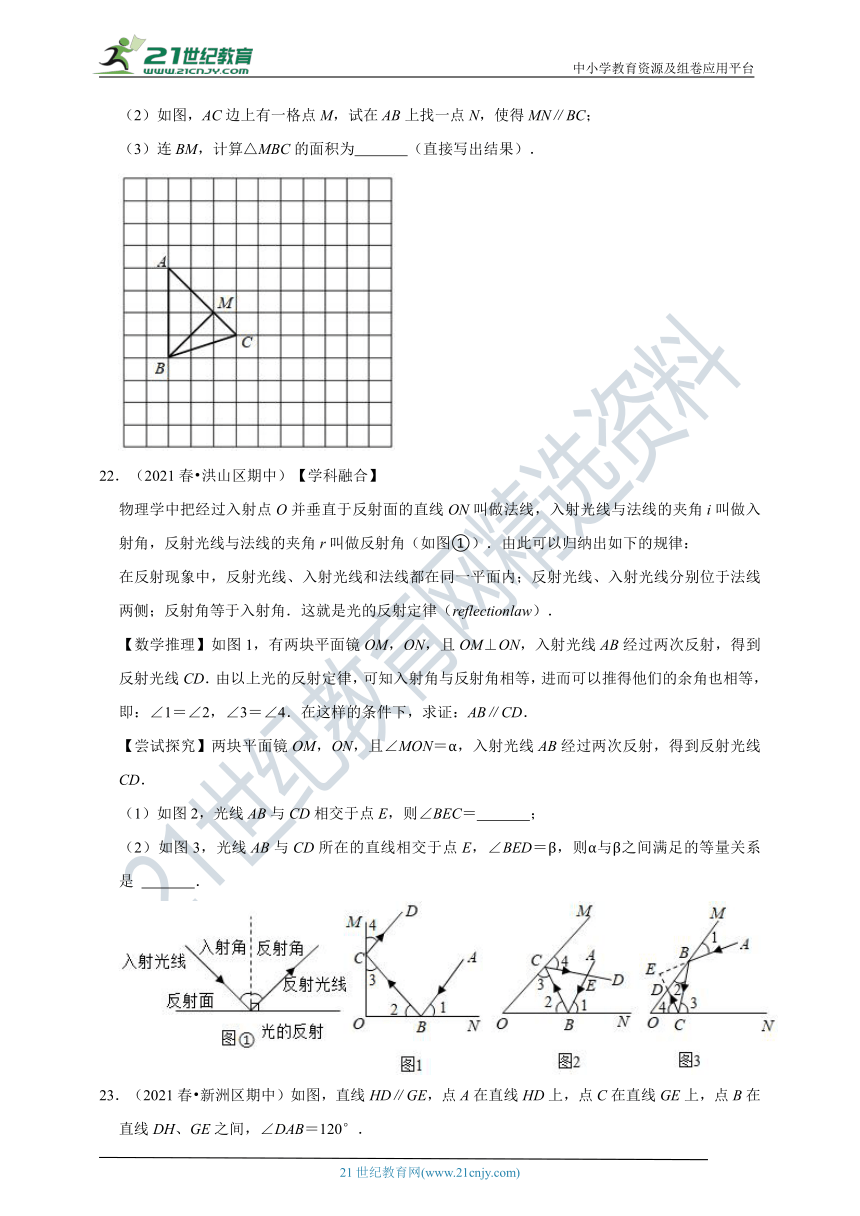
（2）如图，AC边上有一格点M，试在AB上找一点N，使得MN∥BC；
（3）连BM，计算△MBC的面积为　 　（直接写出结果）．
22．（2021春 洪山区期中）【学科融合】
物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）．由此可以归纳出如下的规律：
在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角．这就是光的反射定律（reflectionlaw）．
【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD．由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4．在这样的条件下，求证：AB∥CD．
【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD．
（1）如图2，光线AB与CD相交于点E，则∠BEC＝　 　；
（2）如图3，光线AB与CD所在的直线相交于点E，∠BED＝β，则α与β之间满足的等量关系是 　 　．
23．（2021春 新洲区期中）如图，直线HD∥GE，点A在直线HD上，点C在直线GE上，点B在直线DH、GE之间，∠DAB＝120°．
（1）如图1，若∠BCG＝40°，求∠ABC的度数；
（2）如图2，AF平分∠HAB，BC平分∠FCG，∠BCG＝20°，比较∠B，∠F的大小；
（3）如图3，点P是线段AB上一点，PN平分∠APC，CN平分∠PCE，探究∠HAP和∠N的数量关系，并说明理由．
24．（2021春 官渡区期末）如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足+|b﹣2|＝0．
（1）则C点的坐标为　 　；A点的坐标为　 　．
（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP＝S△ODQ？若存在，请求出t的值；若不存在，请说明理由
（3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．
2021-2022学年下学期武汉初中数学七年级期中典型试卷2
参考答案与试题解析
一．选择题（共10小题）
1．（2021春 洪山区期中）下列实数，，3.14159，﹣，，0.3030030003中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
【考点】无理数；算术平方根；立方根．
【专题】实数；数感．
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【解答】解：是分数，属于有理数；
3.14159，0.3030030003是有限小数，属于有理数；
是整数，属于有理数；
无理数有，，共2个．
故选：B．
【点评】此题考查了无理数的定义．解题的关键是掌握无理数的定义，注意初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
2．（2021春 兴国县期末）下列图案是由图中所示的图案通过平移后得到的是（　　）
A． B． C． D．
【考点】利用平移设计图案．
【专题】平移、旋转与对称；几何直观．
【分析】根据图形平移的性质对各选项进行逐一分析即可．
【解答】解：A、由图中所示的图案通过旋转而成，故本选项错误；
B、由图中所示的图案通过平移而成，故本选项正确；
C、由图中所示的图案通过旋转而成，故本选项错误；
D、由图中所示的图案通过翻折而成，故本选项错误．
故选：B．
【点评】本题考查的是利用平移设计图案，熟知图形平移变换的性质是解答此题的关键．
3．（2012秋 南岸区期末）点P（3，﹣4），则点P在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【考点】点的坐标．
【分析】根据各象限内点的坐标特征解答．
【解答】解：点P（3，﹣4）在第四象限．
故选：D．
【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
4．（2021春 虎林市期末）下列说法不正确的是（　　）
A．的平方根是
B．﹣9是81的一个平方根
C．0.2的算术平方根是0.04
D．﹣27的立方根是﹣3
【考点】立方根；平方根；算术平方根．
【分析】根据平方根的意义，可判断A、B，根据算术平方根的意义．可判断C，根据立方根的意义，可判断D．
【解答】解：A、，故A选项正确；
B、＝﹣9，故B选项正确；
C、＝0.2，故C选项错误；
D、＝﹣3，故D选项正确；
故选：C．
【点评】本题考查了立方根，平方运算是求平方根的关键，立方运算是解立方根的关键．
5．（2021春 江岸区期中）如图，∠1＝∠2，∠3＝112°，则∠4等于（　　）
A．62° B．68° C．78° D．112°
【考点】平行线的判定与性质．
【专题】线段、角、相交线与平行线；推理能力．
【分析】首先证明a∥b，可得∠3＝∠5＝112°，再根据邻补角的性质即可解决问题．
【解答】解：如图，
∵∠1＝∠2，∠2＝∠ABC，
∴∠1＝∠ABC，
∴a∥b，
∴∠3＝∠DEF＝112°，
∴∠4＝180°﹣112°＝68°，
故选：B．
【点评】本题考查平行线的判定和性质，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
6．（2021春 江岸区期中）一个正方形的面积扩大为原来9倍，它的周长变为原来的（　　）倍．
A．2 B．3 C．9 D．12
【考点】算术平方根．
【专题】计算题；运算能力．
【分析】根据一个正方形的面积扩大为原来9倍，可得边长扩大为原来的3倍，要求它的周长变为原来的多少倍，由正方形的周长公式即可求解．
【解答】解：∵一个正方形的面积扩大为原来9倍，
∴它的边长扩大为原来的＝3倍，
∴它的周长变为原来的3倍．
故选：B．
【点评】此题考查了算术平均数，关键是掌握算术平均数的变化规律，用到的知识点是算术平均数、正方形的面积．
7．（2021秋 临渭区期中）已知A点的坐标为（3，a+3），B点的坐标为（a，a﹣4），AB∥y轴，则线段AB的长为（　　）
A．5 B．6 C．7 D．13
【考点】坐标与图形性质．
【专题】平面直角坐标系；推理能力．
【分析】根据平行于y轴的直线上点的横坐标相等，可得a＝3，值根据同一条直线上两点间的距离是大数减小数，可得答案．
【解答】解：由题意得：a＝3，
∴a+3＝6，a﹣4＝﹣1，
A（6，3），B（﹣1，3），
AB＝6﹣（﹣1）＝7，
故选：C．
【点评】本题考查了坐标与图形的性质，由平行于y轴的直线上点的横坐标相等求得a的值是解题关键．
8．（2021春 青山区期中）下列命题中，真命题的个数有（　　）
①无限小数是无理数；
②立方根等于它本身的数有两个，是0和1；
③同位角相等；
④过一点有且只有一条直线与已知直线平行．
A．0个 B．1个 C．2个 D．3个
【考点】命题与定理．
【专题】实数；线段、角、相交线与平行线；数感．
【分析】根据无理数的定义对①进行判断；利用﹣1的立方根为﹣1对②进行判断；根据平行线的性质对③进行判断；根据平行公理可对④进行判断．
【解答】解：无限不循环小数是无理数，所以①为假命题；
立方根等于它本身的数有三个，是0和±1，所以②为假命题；
两直线平行，同位角相等，所以③为假命题；
过直线外一点有且只有一条直线与已知直线平行，所以④为假命题．
故选：A．
【点评】本题考查了命题于定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
9．（2021春 红谷滩区校级期中）已知≈0.5981，≈1.289，≈2.776，则≈（　　）
A．27.76 B．12.89 C．59.81 D．5.981
【考点】立方根．
【专题】实数；运算能力．
【分析】先将化简成含有的式子再计算．
【解答】解：＝＝×＝10≈2.776×10＝27.76．
故选：A．
【点评】本题考查求立方根的计算，解题关键是熟练掌握根式运算方法．
10．（2021春 武昌区期中）如图，一个蒲公英种子从平面直角坐标系的原点O出发，向正东走3米到达点A1，再向正北方向走6米到达点A2，再向正西方向走9米到达点A3，再向正南方向走12米到达点A4，再向正东方向走15米到达点A5，以此规律走下去，当种子到达点A10时，它在坐标系中坐标为（　　）
A．（﹣12，﹣12） B．（15，18） C．（15，﹣12） D．（﹣15，18）
【考点】规律型：点的坐标．
【专题】规律型；推理能力．
【分析】由题意可知：OA1＝3；A1A2＝3×2；A2A3＝3×3；可得规律：An﹣1An＝3n，根据规律可得到A9A10＝3×10＝30，进而求得A10的横纵坐标．
【解答】解：根据题意可知：OA1＝3，A1A2＝6，A2A3＝9，A3A4＝12，A4A5＝15，A5A6＝18 ，A9A10＝30，
∴A1点坐标为（3，0），
A2点坐标为（3，6），
A3点坐标为（﹣6，6），
A4点坐标为（﹣6，﹣6），
A5点坐标为（9，﹣6），
A6点坐标为（9，12），
以此类推，A9点坐标为（15，﹣12），
所以A10点横坐标为15，纵坐标为﹣12+30＝18，
∴A10点坐标为（15，18），
故选：B．
【点评】本题主要考查了坐标确定位置的运用，解题的关键是发现规律，利用规律解决问题，解题时注意：各象限内点P（a，b）的坐标特征为：①第一象限：a＞0，b＞0；②第二象限：a＜0，b＞0；③第三象限：a＜0，b＜0；④第四象限：a＞0，b＜0．
二．填空题（共6小题）
11．（2021春 洪山区期中）若a3＝8，＝2，则a+b＝　6　．
【考点】立方根；算术平方根．
【专题】二次根式；运算能力．
【分析】根据立方根的概念得a的值，根据算术平方根的概念得b的值，然后代入计算可得答案．
【解答】解：∵a3＝8，＝2，
∴a＝2，b＝4，
∴a+b＝2+4＝6．
故答案为：6．
【点评】此题考查的是立方根与平方根，掌握其概念是解决此题关键．
12．（2020秋 宝安区期末）实数a、b在数轴上所对应的点如图所示，则|﹣b|+|a+|+的值　﹣2a﹣b　．
【考点】实数的运算；实数与数轴．
【专题】实数；符号意识．
【分析】直接利用数轴结合绝对值以及平方根的性质化简得出答案．
【解答】解：由数轴可得：a＜﹣，0＜b＜，
故|﹣b|+|a+|+
＝﹣b﹣（a+）﹣a
＝﹣b﹣a﹣﹣a
＝﹣2a﹣b．
故答案为：﹣2a﹣b．
【点评】此题主要考查了实数的运算以及实数与数轴，正确化简各式是解题关键．
13．（2002 泸州）如图，某宾馆在重新装修后，准备在大厅的楼梯上铺上某种红色地毯，已知这种地毯每平方米售价30元，主楼梯道宽2米，其侧面如图所示，则购买地毯至少需要　504　元．
【考点】生活中的平移现象．
【专题】压轴题．
【分析】根据题意，结合图形，先把楼梯的横竖向上向左平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．
【解答】解：如图，利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为5.8米，2.6米，
∴地毯的长度为2.6+5.8＝8.4米，地毯的面积为8.4×2＝16.8平方米，
∴买地毯至少需要16.8×30＝504元．
【点评】解决此题的关键是要利用平移的知识，把要求的所有线段平移到一条直线上进行计算．
14．（2021春 新洲区期中）把一张长方形纸片ABCD沿EF折叠后ED与BC的交点G，D、C分别在M、N的位置上，若∠EFG＝55°，则∠2﹣∠1＝　40°　．
【考点】平行线的性质．
【专题】线段、角、相交线与平行线．
【分析】由折叠的性质可得，∠DEF＝∠GEF，根据平行线的性质可得，∠DEF＝∠EFG＝55°，根据平角的定义即可求得∠1，从而再由平行线的性质求得∠2．
【解答】解：∵AD∥BC，∠EFG＝55°，
∴∠DEF＝∠FEG＝55°，∠1+∠2＝180°，
由折叠的性质可得，∠GEF＝∠DEF＝55°，
∴∠1＝180°﹣∠GEF﹣∠DEF＝180°﹣55°﹣55°＝70°，
∴∠2＝180°﹣∠1＝110°，
∴∠2﹣∠1＝110°﹣70°＝40°．
故答案为：40°．
【点评】此题主要考查折叠的性质以及平行线的性质，解题时注意：两直线平行，同旁内角互补．
15．（2021春 滨江区校级期末）如图a，已知长方形纸带ABCD，将纸带沿EF折叠后，点C、D分别落在H、G的位置，再沿BC折叠成图b，若∠DEF＝72°，则∠GMN＝　72　°．
【考点】平行线的性质．
【专题】矩形 菱形 正方形；平移、旋转与对称；几何直观；推理能力．
【分析】先根据∠DEF＝72°求出∠EFC的度数，进可得出∠EFB和∠BFH的度数，根据∠H＝90°和三角形的内角和可得∠HMF的度数，再由折叠的性质可得∠GMN．
【解答】解：∵AD∥CB，
∴∠EFC+∠DEF＝180°，∠EFB＝∠DEF，
即∠EFC＝180°﹣72°＝108°，∠EFB＝72°，
∴∠BFH＝108°﹣72°＝36°．
∵∠H＝∠D＝90°，
∴∠HMF＝180°﹣90°﹣36°＝54°．
由折叠可得：∠NMF＝∠HMF＝54°，
∴∠GMN＝72°．
故答案为：72．
【点评】本题考查的是平行线的性质，由折叠的性质得到角相等是解题关键．
16．（2021春 江岸区期中）平面直角坐标系中，点M（x，y），N（x﹣2ky，y﹣3kx），MN＝7OM，当点M在y轴正半轴上时，k＝　±　．
【考点】坐标与图形性质．
【专题】平面直角坐标系；运算能力．
【分析】根据M在y轴正半轴上，得出x＝0，得出MN∥x轴，进而求出MN＝|2ky|，OM＝y，列出方程求解即可．
【解答】解：∵M在y轴正半轴上．
∴x＝0，y＞0．
∴OM＝y，N（﹣2ky，y）．
∴MN＝|2ky|．
∴|2ky|＝7y．
∴k＝±．
故答案为：±．
【点评】本题考查了点的坐标，y轴上点的横坐标为0，根据MN＝7OM得出关于k的方程是解题关键．
三．解答题（共8小题）
17．（2021春 青山区期中）计算：
（1）|﹣|+2；
（2）﹣（）2﹣﹣．
【考点】实数的运算．
【专题】实数；运算能力．
【分析】（1）直接去绝对值，再合并数据计算即可；
（2）直接利用立方根以及二次根式的性质分别化简得出答案．
【解答】解：（1）原式＝﹣+2
＝3﹣；
（2）原式＝﹣﹣+2
＝．
【点评】此题主要考查了实数运算，正确化简各数是解题关键．
18．（2021春 青山区期中）如图，直线AB，CD相交于点O，OE把∠BOD分成两部分．
（1）直接写出图中∠AOD的对顶角为　∠BOC　，∠DOE的邻补角为　∠COE　．
（2）若∠AOC＝90°，且∠BOE：∠EOD＝2：3．求∠EOC的度数．
【考点】对顶角、邻补角．
【专题】线段、角、相交线与平行线；运算能力．
【分析】（1）利用对顶角、邻补角的定义直接回答即可；
（2）根据对顶角相等求出∠BOD的度数，再根据∠BOE：∠EOD＝2：3求出∠DOE的度数，然后利用互为邻补角的两个角的和等于180°即可求出∠COE的度数．
【解答】解：（1）∠AOD的对顶角为∠BOC，∠DOE的邻补角为∠COE；
故答案为：∠BOC，∠COE；
（2）∵∠DOB＝∠AOC＝90°，∠DOB＝∠BOE+∠EOD，∠BOE：∠EOD＝2：3，
∴∠EOD＝∠BOE，
∴∠BOE+∠BOE＝90°，
∴∠BOE＝36°，
∴∠DOE＝54°，
∴∠COE＝180°﹣∠DOE＝126°．
【点评】本题主要考查了对顶角，邻补角的定义，利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解．
19．（2021春 武昌区期中）完成下面的推理填空：
如图，已知AB∥CD，∠1＝∠2，∠3＝∠4，求证：∠D＝∠DCE．
证明：∵AB∥CD，
∴∠2＝∠BAE（ 　两直线平行，同位角相等　）．
∵∠BAE＝∠3+　∠CAE　，
∴∠2＝∠3+　∠CAE　，
∵∠3＝∠4，
∴∠2＝∠CAD，
又∵∠2＝　∠1　，
∴∠CAD＝　∠1　，
∴AD∥　BC　（ 　内错角相等，两直线平行　）．
∴∠D＝∠DCE．（ 　两直线平行，内错角相等　）．
【考点】平行线的判定与性质．
【专题】证明题；线段、角、相交线与平行线；推理能力．
【分析】利用平行线的性质和角的和差关系，说明∠1与∠DAC的关系，再利用平行线的性质和判定得结论．
【解答】证明：∵AB∥CD，
∴∠2＝∠BAE（两直线平行，同位角相等）．
∵∠BAE＝∠3+∠CAE，
∴∠2＝∠3+∠CAE，
∵∠3＝∠4，
∴∠2＝∠CAD，
又∵∠2＝∠1，
∴∠CAD＝∠1，
∴AD∥BC（内错角相等，两直线平行）．
∴∠D＝∠DCE（ 两直线平行，内错角相等）．
故答案为：两直线平行，同位角相等；∠CAE；∠CAE；∠1；∠1；BC；内错角相等，两直线平行；两直线平行，内错角相等．
【点评】本题考查了平行线的性质和判定，掌握平行线的性质和判定是解决本题的关键．
20．（2021春 武昌区期中）平面直角坐标系中，将点A、B先向下平移3个单位长度，再向右平移2个单位后，分别得到点A′（3，﹣2）、B′（2，﹣4）．
（1）点A坐标为 　（1，1）　，点B坐标为 　（0，﹣1）　，并在图中标出点A、B；
（2）若点C的坐标为（2，﹣2），求△ABC的面积；
（3）在（2）的条件下，如图所示网格中，点E为图中格点（不与C重合），且使得△ABE与△ABC的面积相等，符合条件的E点有 　5　个．
【考点】三角形综合题．
【专题】三角形；应用意识．
【分析】（1）由平移的性质可求解；
（2）由三角形的面积公式可求解；
（3）由等底等高的三角形的面积相等，可求解．
【解答】解：（1）∵将点A、B先向下平移3个单位长度，再向右平移2个单位后，分别得到点A′（3，﹣2）、B′（2，﹣4）．
∴点A（1，1），点B（0，﹣1），
如图所示，
故答案为（1，1），（0，﹣1）；
（2）S△ABC＝2×3﹣×1×2﹣×1×2﹣×1×3＝；
（3）如图，过点A作BC的平行线，过点B作AC的平行线，两个平行线交于点E3，过点C和点E3作AB的平行线与网格相交于E1，E2，E4，E5四个格点，
∴符合条件的E点有5个，
故答案为：5．
【点评】本题是三角形综合题，考查了平移的性质，三角形的面积公式，平行线的性质等知识，灵活运用这些性质解决问题是本题的关键．
21．（2021春 洪山区期中）在正方形网格中，每个小正方形的边长均为1个单位长度，我们将小正方形的顶点叫做格点，如图，△ABC的三个顶点均在格点上．仅用一把无刻度直尺在给定的网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：
（1）将△ABC先向右平移5个单位长度，再向上平移3个单位长度，得到对应的△A1B1C1，画出平移后的△A1B1C1；
（2）如图，AC边上有一格点M，试在AB上找一点N，使得MN∥BC；
（3）连BM，计算△MBC的面积为　2　（直接写出结果）．
【考点】作图﹣平移变换；平行线的性质．
【专题】作图题；几何直观．
【分析】（1）分别作出A，B，C的对应点A1，B1，C1即可．
（2）利用平行线分线段成比例定理解决问题即可．
（3）根据S△BCM＝S△ABC，求解即可．
【解答】解：（1）如图，△A1B1C1即为所求作．
（2）如图，线段MN即为所求作．
（3）S△BCM＝S△ABC＝××4×3＝2，
故答案为：2．
【点评】本题考查作图﹣平移变换，三角形的面积等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
22．（2021春 洪山区期中）【学科融合】
物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）．由此可以归纳出如下的规律：
在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角．这就是光的反射定律（reflectionlaw）．
【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD．由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4．在这样的条件下，求证：AB∥CD．
【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD．
（1）如图2，光线AB与CD相交于点E，则∠BEC＝　180°﹣2α　；
（2）如图3，光线AB与CD所在的直线相交于点E，∠BED＝β，则α与β之间满足的等量关系是 　β＝2a　．
【考点】平行线的判定；余角和补角；垂线．
【专题】线段、角、相交线与平行线；运算能力．
【分析】【数学推理】根据平面镜反射光线的规律得∠1＝∠2，∠3＝∠4，再利用∠2+∠3＝90°得出∠1+∠2+∠3+∠4＝180°，即可得出∠DCB+∠ABC＝180°，即可证得AB∥CD；
（1）根据三角形内角和定理求得∠2+∠3＝125°，根据平面镜反射光线的规律得∠1＝∠2，∠3＝∠4，再利用∠DCB＝180°﹣2∠3，∠ABC＝180°﹣2∠2，得∠BEC＝180°﹣∠ABC﹣∠BCD；
（2）利用平角的定义得出∠ABC＝180°﹣2∠2，∠BCD＝180°﹣2∠3，利用外角的性质∠BED＝∠ABC﹣∠BCD＝（180°﹣2∠2）﹣（180°﹣2∠3）＝2（∠3﹣∠2）＝β，而∠BOC＝∠3﹣∠2＝α，即可证得β＝2α．
【解答】解：如图1，∵OM⊥ON，
∴∠CON＝90°，
∴∠2+∠3＝90°，
∵∠1＝∠2，∠3＝∠4，
∴∠1+∠2+∠3+∠4＝180°，
∠DCB+∠ABC＝180°，
AB∥CD；
【尝试探究】
（1）如图2，在△OBC中，∵∠MON＝α，
∴∠2+∠3＝180°﹣α，
∵∠1＝∠2，∠3＝∠4，
∴∠DCB＝180°﹣2∠3，∠ABC＝180°﹣2∠2，
∴∠BEC＝180°﹣∠ABC﹣∠BCD
＝180°﹣（180°﹣2∠2）﹣（180°﹣2∠3）
＝2（∠2+∠3）﹣180°
＝2（180°﹣a）﹣180°
＝180°﹣2α，
故答案为：180°﹣2α；
（2）如图4，B＝2a，
理由如下：∵∠1＝∠2，∠3＝∠4，
∴∠ABC＝180°﹣2∠2，
∠BCD＝180°﹣2∠3，
∴∠D＝∠ABC﹣∠BCD
＝（180°﹣2∠2）﹣（180°﹣2∠3）
＝2（∠3﹣∠2）＝∠β，
∵∠BOC＝∠3﹣∠2＝a，
∴β＝2a．
故答案为：β＝2a．
【点评】本题考查了平行线的判定，三角形外角的性质以及三角形内角和定理，熟练掌握三角形的性质是解题的关键．
23．（2021春 新洲区期中）如图，直线HD∥GE，点A在直线HD上，点C在直线GE上，点B在直线DH、GE之间，∠DAB＝120°．
（1）如图1，若∠BCG＝40°，求∠ABC的度数；
（2）如图2，AF平分∠HAB，BC平分∠FCG，∠BCG＝20°，比较∠B，∠F的大小；
（3）如图3，点P是线段AB上一点，PN平分∠APC，CN平分∠PCE，探究∠HAP和∠N的数量关系，并说明理由．
【考点】平行线的性质．
【专题】线段、角、相交线与平行线；运算能力；推理能力．
【分析】（1）过点B作BM∥HD，则HD∥GE∥BM，根据平行线的性质求得∠ABM与∠CBM，便可求得最后结果；
（2）过B作BP∥HD∥GE，过F作FQ∥HD∥GE，由平行线的性质得，∠ABC＝∠HAB+∠BCG，∠AFC＝∠HAF+∠FCG，由角平分线的性质和已知角的度数分别求得∠HAF，∠FCG，最后便可求得结果；
（3）过P作PK∥HD∥GE，先由平行线的性质证明∠ABC＝∠HAB+∠BCG，∠AFC＝∠HAF+∠FCG，再根据角平分线求得∠NPC与∠PCN，由后由三角形内角和定理便可求得结果．
【解答】解：（1）过点B作BM∥HD，则HD∥GE∥BM，如图1，
∴∠ABM＝180°﹣∠DAB，∠CBM＝∠BCG，
∵∠DAB＝120°，∠BCG＝40°，
∴∠ABM＝60°，∠CBM＝40°，
∴∠ABC＝∠ABM+∠CBM＝100°；
（2）过B作BP∥HD∥GE，过F作FQ∥HD∥GE，如图2，
∴∠ABP＝∠HAB，∠CBP＝∠BCG，∠AFQ＝∠HAF，∠CFQ＝∠FCG，
∴∠ABC＝∠HAB+∠BCG，∠AFC＝∠HAF+∠FCG，
∵∠DAB＝120°，
∴∠HAB＝180°﹣120°＝60°，
∵AF平分∠HAB，BC平分∠FCG，∠BCG＝20°，
∴∠HAF＝30°，∠FCG＝40°，
∴∠ABC＝60°+20°＝80°，
∠AFC＝30°+40°＝70°，
∴∠ABC＞∠AFC；
（3）过P作PK∥HD∥GE，如图3，
∴∠APK＝∠HAP，∠CPK＝∠PCG，
∴∠APC＝∠HAP+∠PCG，
∵PN平分∠APC，
∴∠NPC＝∠HAP+∠PCG，
∵∠PCE＝180°﹣∠PCG，CN平分∠PCE，
∴∠PCN＝＝90°﹣∠PCG，
∵∠N+∠NPC+∠PCN＝180°，
∴∠N＝180°﹣∠HAP﹣∠PCG﹣90°+∠PCG＝90°﹣∠HAP，
即，∠N＝90°﹣∠HAP．
【点评】本题考查了角平分线的定义，平行线性质和判定：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用，理清各角度之间的关系是解题的关键，也是本题的难点．
24．（2021春 官渡区期末）如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足+|b﹣2|＝0．
（1）则C点的坐标为　（2，0）　；A点的坐标为　（0，4）　．
（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP＝S△ODQ？若存在，请求出t的值；若不存在，请说明理由
（3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．
【考点】坐标与图形性质；平行线的性质；三角形的面积；非负数的性质：绝对值；非负数的性质：算术平方根．
【专题】方程思想．
【分析】（1）根据绝对值和算术平方根的非负性，求得a，b的值即可；
（2）先得出CP＝t，OP＝2﹣t，OQ＝2t，AQ＝4﹣2t，再根据S△ODP＝S△ODQ，列出关于t的方程，求得t的值即可；
（3）过H点作AC的平行线，交x轴于P，先判定OG∥AC，再根据角的和差关系以及平行线的性质，得出∠PHO＝∠GOF＝∠1+∠2，∠OHC＝∠OHP+∠PHC＝∠GOF+∠4＝∠1+∠2+∠4，最后代入进行计算即可．
【解答】解：（1）∵+|b﹣2|＝0，
∴a﹣2b＝0，b﹣2＝0，
解得a＝4，b＝2，
∴A（0，4），C（2，0）；
（2）由条件可知：P点从C点运动到O点时间为2秒，Q点从O点运动到A点时间为2秒，
∴0＜t≤2时，点Q在线段AO上，
即 CP＝t，OP＝2﹣t，OQ＝2t，AQ＝4﹣2t，
∴，，
∵S△ODP＝S△ODQ，
∴2﹣t＝t，
∴t＝1；
（3）的值不变，其值为2．
∵∠2+∠3＝90°，
又∵∠1＝∠2，∠3＝∠FCO，
∴∠GOC+∠ACO＝180°，
∴OG∥AC，
∴∠1＝∠CAO，
∴∠OEC＝∠CAO+∠4＝∠1+∠4，
如图，过H点作AC的平行线，交x轴于P，则∠4＝∠PHC，PH∥OG，
∴∠PHO＝∠GOF＝∠1+∠2，
∴∠OHC＝∠OHP+∠PHC＝∠GOF+∠4＝∠1+∠2+∠4，
∴．
【点评】本题主要考查了坐标与图形性质，解决问题的关键值作辅助线构造平行线．解题时注意：任意一个数的绝对值都是非负数，算术平方根具有非负性，非负数之和等于0时，各项都等于0．
考点卡片
1．非负数的性质：绝对值
在实数范围内，任意一个数的绝对值都是非负数，当几个数或式的绝对值相加和为0时，则其中的每一项都必须等于0．
根据上述的性质可列出方程求出未知数的值．
2．平方根
（1）定义：如果一个数的平方等于a，这个数就叫做a的平方根，也叫做a的二次方根．
一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根．
（2）求一个数a的平方根的运算，叫做开平方．
一个正数a的正的平方根表示为“”，负的平方根表示为“﹣”．
正数a的正的平方根，叫做a的算术平方根，记作．零的算术平方根仍旧是零．
平方根和立方根的性质
1．平方根的性质：正数a有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
2．立方根的性质：一个数的立方根只有一个，正数的立方根是正数，负数的立方根是负数，0的立方根是0．
3．算术平方根
（1）算术平方根的概念：一般地，如果一个正数x的平方等于a，即x2＝a，那么这个正数x叫做a的算术平方根．记为．
（2）非负数a的算术平方根a有双重非负性：①被开方数a是非负数；②算术平方根a本身是非负数．
（3）求一个非负数的算术平方根与求一个数的平方互为逆运算，在求一个非负数的算术平方根时，可以借助乘方运算来寻找．
4．非负数的性质：算术平方根
（1）非负数的性质：算术平方根具有非负性．
（2）利用算术平方根的非负性求值的问题，主要是根据被开方数是非负数，开方的结果也是非负数列出不等式求解．非负数之和等于0时，各项都等于0利用此性质列方程解决求值问题．
5．立方根
（1）定义：如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根．这就是说，如果x3＝a，那么x叫做a的立方根．记作：．
（2）正数的立方根是正数，0的立方根是0，负数的立方根是负数．即任意数都有立方根．
（3）求一个数a的立方根的运算叫开立方，其中a叫做被开方数．
注意：符号a3中的根指数“3”不能省略；对于立方根，被开方数没有限制，正数、零、负数都有唯一一个立方根．
【规律方法】平方根和立方根的性质
1．平方根的性质：正数a有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
2．立方根的性质：一个数的立方根只有一个，正数的立方根是正数，负数的立方根是负数，0的立方根是0．
6．无理数
（1）、定义：无限不循环小数叫做无理数．
说明：无理数是实数中不能精确地表示为两个整数之比的数，即无限不循环小数． 如圆周率、2的平方根等．
（2）、无理数与有理数的区别：
　①把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数，
　　比如4＝4.0，13＝0.33333…而无理数只能写成无限不循环小数，比如2＝1.414213562．
　②所有的有理数都可以写成两个整数之比；而无理数不能．
（3）学习要求：会判断无理数，了解它的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，如分数π2是无理数，因为π是无理数．
无理数常见的三种类型
（1）开不尽的方根，如等．
（2）特定结构的无限不循环小数，
如0.303 003 000 300 003…（两个3之间依次多一个0）．
（3）含有π的绝大部分数，如2π．
注意：判断一个数是否为无理数，不能只看形式，要看化简结果．如是有理数，而不是无理数．
7．实数与数轴
（1）实数与数轴上的点是一一对应关系．
任意一个实数都可以用数轴上的点表示；反之，数轴上的任意一个点都表示一个实数．数轴上的任一点表示的数，不是有理数，就是无理数．
（2）在数轴上，表示相反数的两个点在原点的两旁，并且两点到原点的距离相等，实数a的绝对值就是在数轴上这个数对应的点与原点的距离．
（3）利用数轴可以比较任意两个实数的大小，即在数轴上表示的两个实数，右边的总比左边的大，在原点左侧，绝对值大的反而小．
8．实数的运算
（1）实数的运算和在有理数范围内一样，值得一提的是，实数既可以进行加、减、乘、除、乘方运算，又可以进行开方运算，其中正实数可以开平方．
（2）在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．
另外，有理数的运算律在实数范围内仍然适用．
【规律方法】实数运算的“三个关键”
1．运算法则：乘方和开方运算、幂的运算、指数（特别是负整数指数，0指数）运算、根式运算、特殊三角函数值的计算以及绝对值的化简等．
2．运算顺序：先乘方，再乘除，后加减，有括号的先算括号里面的，在同一级运算中要从左到右依次运算，无论何种运算，都要注意先定符号后运算．
3．运算律的使用：使用运算律可以简化运算，提高运算速度和准确度．
9．点的坐标
（1）我们把有顺序的两个数a和b组成的数对，叫做有序数对，记作（a，b）．
（2）平面直角坐标系的相关概念
①建立平面直角坐标系的方法：在同一平面内画；两条有公共原点且垂直的数轴．
②各部分名称：水平数轴叫x轴（横轴），竖直数轴叫y轴（纵轴），x轴一般取向右为正方向，y轴一般取象上为正方向，两轴交点叫坐标系的原点．它既属于x轴，又属于y轴．
（3）坐标平面的划分
建立了坐标系的平面叫做坐标平面，两轴把此平面分成四部分，分别叫第一象限，第二象限，第三象限，第四象限．坐标轴上的点不属于任何一个象限．
（4）坐标平面内的点与有序实数对是一一对应的关系．
10．规律型：点的坐标
规律型：点的坐标．
11．坐标与图形性质
1、点到坐标轴的距离与这个点的坐标是有区别的，表现在两个方面：①到x轴的距离与纵坐标有关，到y轴的距离与横坐标有关；②距离都是非负数，而坐标可以是负数，在由距离求坐标时，需要加上恰当的符号．
2、有图形中一些点的坐标求面积时，过已知点向坐标轴作垂线，然后求出相关的线段长，是解决这类问题的基本方法和规律．
3、若坐标系内的四边形是非规则四边形，通常用平行于坐标轴的辅助线用“割、补”法去解决问题．
12．余角和补角
（1）余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．
（2）补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．
（3）性质：等角的补角相等．等角的余角相等．
（4）余角和补角计算的应用，常常与等式的性质、等量代换相关联．
注意：余角（补角）与这两个角的位置没有关系．不论这两个角在哪儿，只要度数之和满足了定义，则它们就具备相应的关系．
13．对顶角、邻补角
（1）对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．
（2）邻补角：只有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．
（3）对顶角的性质：对顶角相等．
（4）邻补角的性质：邻补角互补，即和为180°．
（5）邻补角、对顶角成对出现，在相交直线中，一个角的邻补角有两个．邻补角、对顶角都是相对与两个角而言，是指的两个角的一种位置关系．它们都是在两直线相交的前提下形成的．
14．垂线
（1）垂线的定义
当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．
（2）垂线的性质
在平面内，过一点有且只有一条直线与已知直线垂直．
注意：“有且只有”中，“有”指“存在”，“只有”指“唯一”
“过一点”的点在直线上或直线外都可以．
15．平行线的判定
（1）定理1：两条直线被第三条所截，如果同位角相等，那么这两条直线平行． 简单说成：同位角相等，两直线平行．
（2）定理2：两条直线被第三条所截，如果内错角相等，那么这两条直线平行．简单说成：内错角相等，两直线平行．
（3 ）定理3：两条直线被第三条所截，如果同旁内角互补，那么这两条直线平行．简单说成：同旁内角互补，两直线平行．
（4）定理4：两条直线都和第三条直线平行，那么这两条直线平行．
（5）定理5：在同一平面内，如果两条直线同时垂直于同一条直线，那么这两条直线平行．
16．平行线的性质
1、平行线性质定理
定理1：两条平行线被第三条直线所截，同位角相等． 简单说成：两直线平行，同位角相等．
定理2：两条平行线被地三条直线所截，同旁内角互补．．简单说成：两直线平行，同旁内角互补．
定理3：两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．
2、两条平行线之间的距离处处相等．
17．平行线的判定与性质
（1）平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．
（2）应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．
（3）平行线的判定与性质的联系与区别
区别：性质由形到数，用于推导角的关系并计算；判定由数到形，用于判定两直线平行．
联系：性质与判定的已知和结论正好相反，都是角的关系与平行线相关．
（4）辅助线规律，经常作出两平行线平行的直线或作出联系两直线的截线，构造出三类角．
18．三角形的面积
（1）三角形的面积等于底边长与高线乘积的一半，即S△＝×底×高．
（2）三角形的中线将三角形分成面积相等的两部分．
19．三角形综合题
三角形综合题．
20．命题与定理
1、判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．
2、有些命题的正确性是用推理证实的，这样的真命题叫做定理．
3、定理是真命题，但真命题不一定是定理．
4、命题写成“如果…，那么…”的形式，这时，“如果”后面接的部分是题设，“那么”后面解的部分是结论．
5、命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
21．生活中的平移现象
1、平移的概念
在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，简称平移．
2、平移是指图形的平行移动，平移时图形中所有点移动的方向一致，并且移动的距离相等．
3、确定一个图形平移的方向和距离，只需确定其中一个点平移的方向和距离．
22．作图-平移变换
（1）确定平移后图形的基本要素有两个：平移方向、平移距离．
（2）作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
23．利用平移设计图案
确定一个基本图案按照一定的方向平移一定的距离，连续作图即可设计出美丽的图案．
通过改变平移的方向和距离可使图案变得丰富多彩．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)

展开更多......

收起↑