资源简介

(共18张PPT)
6.1 定积分的概念与性质
一、定积分概念的引入—两个实例
实例1 曲边梯形面积的计算
曲边梯形是指由三条直线段(其中两条互相平行，第三条(叫做底边)与前两条垂直)和一条曲线弧(叫做曲边，曲边与任意一条垂直于底边的直线至多只交于一点)围成的封闭的平面图形(如图6-2)．
任意曲线围成的平面图形的面积计算，都可以归结为曲边梯形面积的计算，所以，首先研究曲边梯形的面积．
图6-2
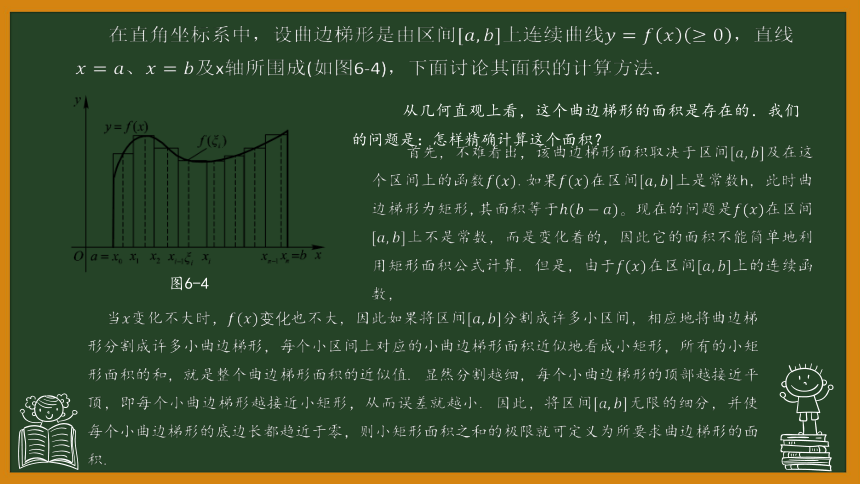
在直角坐标系中，设曲边梯形是由区间上连续曲线直线
及x轴所围成(如图6-4)，下面讨论其面积的计算方法．
图6-4
从几何直观上看，这个曲边梯形的面积是存在的．我们的问题是：怎样精确计算这个面积？
首先，不难看出，该曲边梯形面积取决于区间及在这个区间上的函数.如果在区间上是常数h，此时曲边梯形为矩形,其面积等于现在的问题是在区间上不是常数，而是变化着的，因此它的面积不能简单地利用矩形面积公式计算. 但是，由于在区间上的连续函数，
当变化不大时，也不大，因此如果将区间分割成许多小区间，相应地将曲边梯形分割成许多小曲边梯形，每个小区间上对应的小曲边梯形面积近似地看成小矩形，所有的小矩形面积的和，就是整个曲边梯形面积的近似值. 显然分割越细，每个小曲边梯形的顶部越顶，即每个小曲边梯形越接近小矩形，从而误差就越小. 因此，将区间无限的细分，并使每个小曲边梯形的底边长都趋近于零，则小矩形面积之和的极限就可定义为所要求曲边梯形的面积.
根据以上分析，曲边梯形的面积可按下述步骤来计算：
(1)分割（大化小）：任取分点 ，把区间 分成n个小区间
，每个小区间的长度记作 ，过每一个分点
作垂直于x轴的直线段，把曲边梯形分成n个小曲边梯形，每个小曲边梯形的面积记作 .
(2)近似（直代曲）：在每个小区间 上任取一点 ,以 为底， 为高的小矩形的面积
作为相应的小曲边梯形面积 的近似值，即
(3)求和（近似和）：把n个小曲边梯形面积的近似值累加起来，就得到曲边梯形面积A的近似值，即
(4)取极限：若记 ， 则当 时，所有小区间的长度都趋于零．如果上述和式的极限存在，这个极限值就是曲边梯形面积的精确值，即
实例2 变速直线运动的路程
设一质点作变速直线运动，已知速度 是时间 在区间 上的连续函数，且 ，计算质点在这段时间内经过的路程 。
由于速度是变量，即速度 是随着时间 而变化，因此，路程s不能直接用“速度×时间”来计算. 但是，若把时间区间 分成许多小时间段，因质点运动的速度是连续变化的，则在每个小段时间内，速度变化不大，可以近似地看作是匀速的. 于是，在时间间隔很短的条件下，可以用“匀速”近似地代替“变速”，从而求得每一小段时间内路程s的近似值，将各小段上的路程的近似值相加，可得到整个时间段内路程s的近似值. 最后通过对时间间隔无限细分即取极限就可得到路程s的精确值．
具体计算步骤如下：
(1)分割（大化小）：任取分点 ，把区间 分成n个小区间
，记每个小区间的长度为 ；
(3)求和（近似和）：把n段时间上的路程的近似值相加，即得到总路程的近似值，即
(2)近似（常代变）：任取一时刻 ，用 来代替 上各个时刻的速度（看成匀速运动），于是在时间间隔 内质点所走过的路程 的近似值为
(4)取极限：若记 ，则当 时，所有时间区间的长度都趋于零．如果上述和式的极限存在，这个极限值就是质点在时间间隔 上所经过的路程s的精确值，即
二、定积分的定义
定义 设函数 在区间 上有定义，在 中任意插入n-1个分点
，把区间 任意分割成n个小区间
，小区间的长度记作 ，记 ，在
每个小区间 上任取一点 ，作和式 .当 时，
若极限 存在 （这个极限值与区间 的分法及点 的取法无
关），则称函数 在 上可积，并称这个极限为函数 在区间 上
的定积分，记作 ，即
其中，x称为积分变量， 成为被积函数， 成为被积表达式， 称为积
分下限， 成为积分上限， 称为积分区间.
根据定积分的定义，前面所讨论的两个实际问题可分别表述如下：
(2)速度为 的质点在时间段 上经过路程s等于速度函数 在时间段
上的定积分，即
(1)曲线 ， 轴与直线 和 所围城的曲边梯形的面积A等于
在区间 上的定积分，即
关于定积分的定义作以下几点说明：
(1)闭区间上的连续函数是可积的；闭区间上只有有限个间断点的有界函数也是可积的.
(2)定积分 是一个数值，它的大小仅与被积函数 和积分区间 有关，而与积分区间的分法、点 的选取方法及积分变量的符号无关，即
(3)我们规定：
(4)“分割-近似-求和-取极限”是定积分的思想方法.
三、定积分的几何意义
1、如果函数 在区间 上连续，且 ，则定积分 在
几何上表示由曲线 与直线 所围成的曲边梯形的面
积A，即 .
2、如果函数 在区间 上连续，且 ，则定积分 在
几何上表示由曲线 与直线 所围成的曲边梯形面积
的相反数，即 .
3、如果函数 在区间 上即取正值又取负值，则定积分 在
几何上表示由曲线 与直线 所围成的曲边梯形面积
的代数和（如图所示），即 .
例1 用定积分表示图中阴影部分面积.
解：图1中阴影部分是由曲线 与直线 及x轴所围，且在x轴上方，由定积分的几何意义知阴影部分面积
图1
图2
图3
图2中阴影部分是由曲线 与直线 及x轴所围，由定积分的几何意义知阴影部分面积
图3中阴影部分是由椭圆 所围，根据对称性，阴影部分的面积为：
例2 用定积分几何意义求下列积分.
解：
图1
图2
四、定积分的性质
由定义知，定积分是和式的极限，由极限的运算法则，可推导出定积分的性质.涉及到的函数在所给定的区间上都是可积的.
性质2 若 在区间 上可积，k为任意常数，则 在 上也可积，且
性质1 若 在区间 上可积，则 在 区间上也可积，且
性质1和性质2合称为线性性质，写为
性质3（可加性） 对任意的点 ，有
性质3中c的任意性意味着不论c是[a,b]之内，还是[a,b]之外，这个性质均成立.
例 利用定积分几何意义求
解:因为 ，由定积分的几何意义知，
所以
随堂练习
解:
利用定积分几何意义，求
性质4 如果被积函数 ，则 .
特别地，当 时，有 .
性质5 (积分的保序性)如果在区间 上，恒有 ，则
推论1 设 在区间 上可积，若 ，则 .
若 ，则 .
推论2 设 在区间 上可积，且 ，则 .
例 因为在区间 上有 ，由定积分的保序性，得 .
因为在区间 上 ，所以 .
因为在区间 上 ，所以 .
性质6 (积分估值不等式)如果函数 在区间 上有最大值M和最小值m，
则
例 估计定积分 的值.
解:设 ， ，令 ，得驻点 ，比较 及区间
端点 的函数值，有 .
函数 在区间 上连续，则 在 上的最小值为 ，
最大值为M=1，由定积分的估值不等式，得
性质7的几何意义是：由曲线 与直线 和x轴所围成的曲边
梯形的面积等于区间 上某个矩形的面积.这个矩形的底是区间 ， 矩形
的高为区间 内某一点 处的函数值 .
性质7(积分中值定理)如果函数 在区间 上连续，则在(a,b)内至少有一点 ，使得
显然，由性质7可得
例如
性质8(对称区间上奇偶函数的积分性质)设 在对称区间 上连续，则
(1)如果 为奇函数，则 ；
(1)如果 为偶函数，则 .

展开更多......

收起↑