 资源预览
资源预览

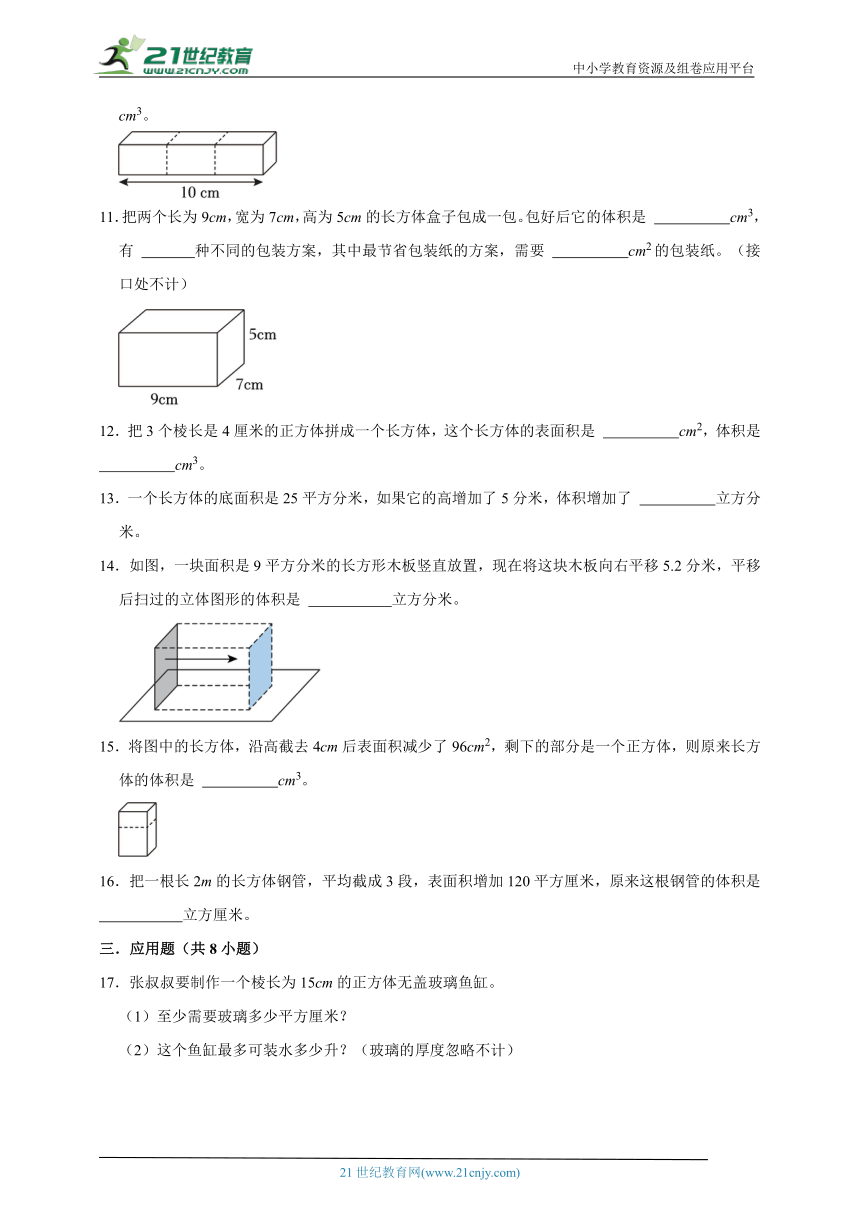



 资源预览
资源预览




