资源简介

2025年中考数学二轮复习考前预测：锐角三角函数
一．选择题（共10小题）
1．（2025 福建模拟）在Rt△ABC中，∠B＝90°．已知AB＝6，AC＝10，则sinA的值为（　　）
A． B． C． D．
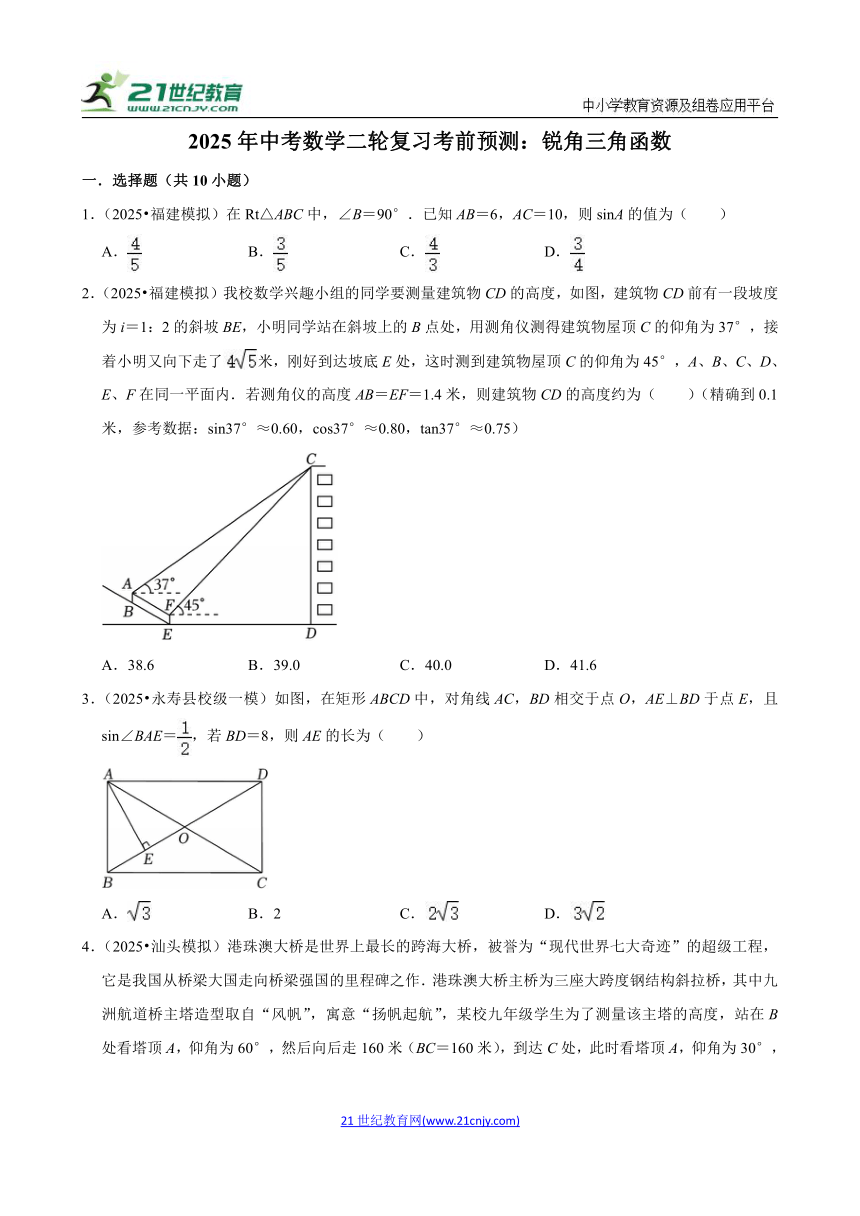
2．（2025 福建模拟）我校数学兴趣小组的同学要测量建筑物CD的高度，如图，建筑物CD前有一段坡度为i＝1：2的斜坡BE，小明同学站在斜坡上的B点处，用测角仪测得建筑物屋顶C的仰角为37°，接着小明又向下走了米，刚好到达坡底E处，这时测到建筑物屋顶C的仰角为45°，A、B、C、D、E、F在同一平面内．若测角仪的高度AB＝EF＝1.4米，则建筑物CD的高度约为（　　）（精确到0.1米，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A．38.6 B．39.0 C．40.0 D．41.6
3．（2025 永寿县校级一模）如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，且sin∠BAE＝，若BD＝8，则AE的长为（　　）
A． B．2 C． D．
4．（2025 汕头模拟）港珠澳大桥是世界上最长的跨海大桥，被誉为“现代世界七大奇迹”的超级工程，它是我国从桥梁大国走向桥梁强国的里程碑之作．港珠澳大桥主桥为三座大跨度钢结构斜拉桥，其中九洲航道桥主塔造型取自“风帆”，寓意“扬帆起航”，某校九年级学生为了测量该主塔的高度，站在B处看塔顶A，仰角为60°，然后向后走160米（BC＝160米），到达C处，此时看塔顶A，仰角为30°，则该主塔的高度是（　　）
A．80米 B．米 C．160米 D．米
5．（2025 登封市一模）如图所示，在矩形网格中，每个小正方形的边长为1，△ABC的三个顶点都在格点上，则tanA的值为（　　）
A． B． C． D．
6．（2025 潍坊模拟）在凡尔纳的小说《神秘岛》中，有一段工程师和赫伯特一起测量瞭望塔的高度的情节．工程师先做了一个悬垂，其实就是在绳子的一端栓了一块石头，工程师让赫伯特拿着，然后拿起一根木杆，长度大概为12英尺，两个人一前一后向瞭望塔走去，两个人来到距离瞭望塔485英尺的一个地方，工程师把木杆的一头插到土里，插下去的深度大概是2英尺，接着，工程师从赫伯特手里结果悬垂，对木杆进行校正，知道木杆完全竖直，之后对木杆插到土里的部分进行固定，固定好木杆后，工程师朝着远离木杆的方向走了15英尺，仰面平躺在了地面上（眼睛离木杆15英尺），并且让自己的眼睛能够正好通过木杆的尖端看到瞭望塔的最顶端，工程师在这个点上做了一个标记，如图所示，请你求出此时瞭望塔的高度是（　　）
A．333英尺 B．英尺 C．400英尺 D．英尺
7．（2025 静安区一模）如果锐角A的余弦值为，下列关于锐角A的取值范围的说法中，正确的是（　　）
A．0°＜∠A＜30° B．30°＜∠A＜45°
C．45°＜∠A＜60° D．60°＜∠A＜90°
8．（2025 青浦区一模）如图，点P是航拍飞机在某一高度时的位置，BH是地平线，PH⊥BH，PC∥BH，AB是某大型建筑物的斜面．从点P观测点B的俯角是（　　）
A．∠HPB B．∠CPB C．∠APB D．∠PBA
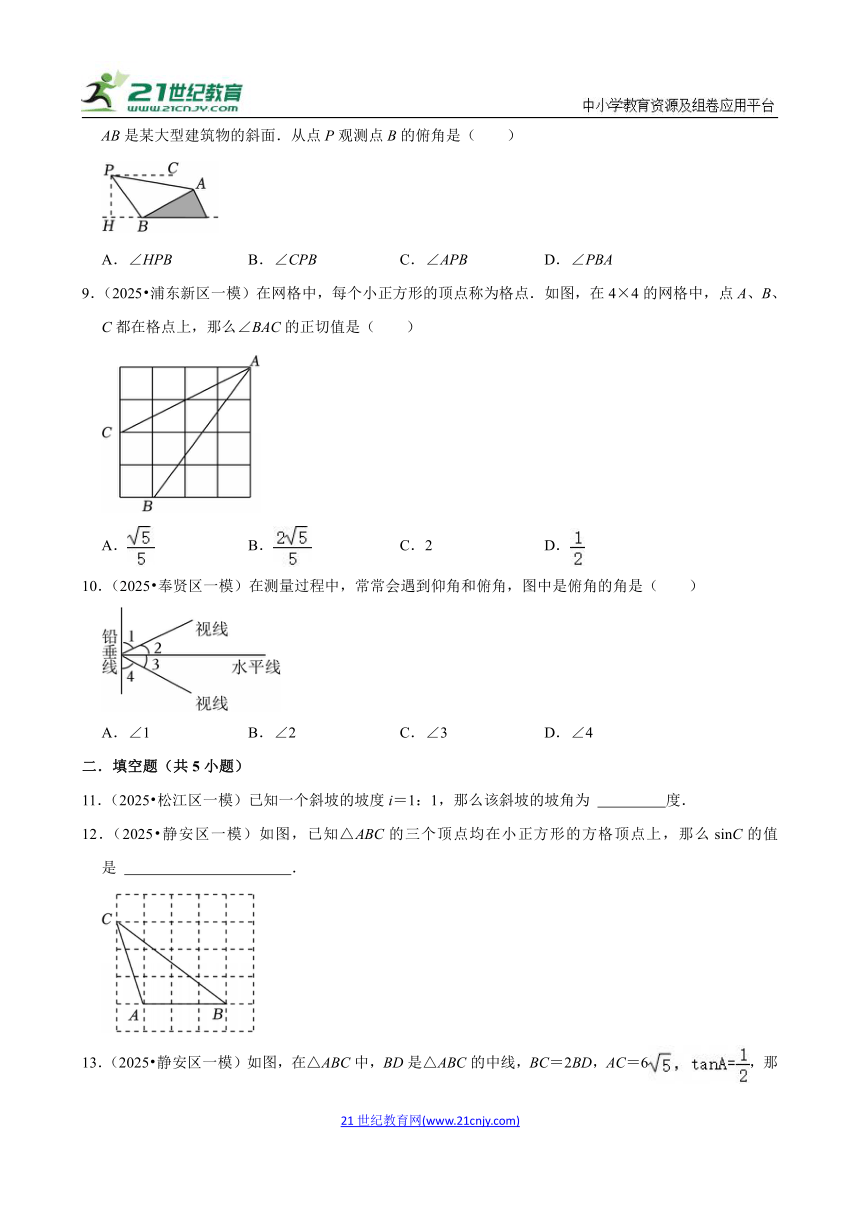
9．（2025 浦东新区一模）在网格中，每个小正方形的顶点称为格点．如图，在4×4的网格中，点A、B、C都在格点上，那么∠BAC的正切值是（　　）
A． B． C．2 D．
10．（2025 奉贤区一模）在测量过程中，常常会遇到仰角和俯角，图中是俯角的角是（　　）
A．∠1 B．∠2 C．∠3 D．∠4
二．填空题（共5小题）
11．（2025 松江区一模）已知一个斜坡的坡度i＝1：1，那么该斜坡的坡角为 　 　度．
12．（2025 静安区一模）如图，已知△ABC的三个顶点均在小正方形的方格顶点上，那么sinC的值是 　 　．
13．（2025 静安区一模）如图，在△ABC中，BD是△ABC的中线，BC＝2BD，AC＝6，那么AB的长为 　 　．
14．（2025 徐汇区一模）如图，热气球探测器显示，从热气球A处测得一栋楼顶部C处的仰角是37°，测得这栋楼的底部B处的俯角是60°，热气球与这栋楼的水平距离是30米，那么这栋楼的高度是 　 　米（精确到0.1米）．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，）
15．（2025 青浦区一模）如图，梯形ABCD是某水库大坝的横截面．已知坝高AE＝8m，如果将坡度为1：的斜坡AB改为坡度为1：2的斜坡AP，那么大坝底部应加宽 　 　m．（结果保留根号）
三．解答题（共5小题）
16．（2025 鼓楼区校级模拟）物流中心A与三个菜鸟驿站B、C、D的平面示意图如图．D在A的正南方，C在A的东南方向上且在D的北偏东30°方向上，B在A的正东方且∠ABC＝37°，已知AB＝5.6km．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，≈1.73）．
（1）求驿站B、C之间的距离；
（2）派送员小外计划9：00从A出发沿着A→B→C→D的路线派送快递到三个驿站，上午9：50完成快递派送．但导航显示AB路段拥堵严重，于是他改变路线（9：00出发），沿着A→D→C→B的路线派送快递到三个驿站．若AD路段行驶的平均速度为40km/h，其余路段的平均行驶速度为30km/h且小外在每个驿站均停留7min存放快递．请通过计算说明他能否在9：50之前完成派送．
17．（2025 雁塔区校级模拟）随着农业现代化的进一步推进，新农村的积极建设，农民伯伯可用无人机进行药物喷洒来消灭虫害．如图，这是一位农民伯伯喷药过程中的实时画面示意图，他在水平地面上点A处测得无人机的位置点D的仰角为53°．当他迎着坡度为8：15的斜坡从点A走到点B时，无人机恰好从点D沿着水平方向飞到点C此时，他在点B处测得点C的仰角∠CBE为45°．已知AB＝34米，CD＝50米，这位农民伯伯让无人机沿与水平地面平行的方向飞行以便喷洒均匀．点A，B，C，D，E，F在同一竖直平面内，求此时无人机的位置点C距水平地面AF的高度．（测角仪的高度忽略不计．参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈）
18．（2025 雁塔区校级一模）小新的数学研学日记
课题：测量旗杆的高度
地点：操场
时间：2025月1月13日
昨天，晴．高老师要带我们去操场测量旗杆的高度，我们小组设计方案：小卓拿着标杆垂直于地面放置，我和小越用卷尺测量标杆、标杆的影长和旗杆的影长，如图1所示，标杆AB＝a，影长BC＝b，旗杆的影长DF＝c，则可求得旗杆DE的高度为 　 　．
今天，阴．设计方案：如图2所示，高老师将升旗用绳子拉直，使绳子的底端G刚好触到地面，用仪器测得绳子与地面的夹角为37°，然后又将绳子拉到一个0.3米高的平台上，拉直绳子使绳子上的H点刚好触到平台时剩余的绳子长度为5米，此时测得绳子与平台的夹角为54°，利用这些数据能求出旗杆DE的高度吗？
请你回答小新的问题．若能，请求出旗杆的高度；若不能，请说明理由．
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，sin54°≈0.8，cos54°≈0.58，tan54°≈1.45）
19．（2025 济南模拟）如图，某校教学楼后面紧邻着一个山坡，山坡面是一块平地，BC∥AD，BE⊥AD，斜坡AB长26m，斜坡AB的坡比为2.4：1．
（1）求坡高BE；
（2）本学期初三学生开展数学学科“综合与实践”活动，主题：测量高度A小组选择测量教学楼高度，他们的做法是：在教学楼F处安置测倾器，测得此时B的仰角∠BFG＝α和A的俯角∠AFG＝β，然后借助已知中的数据计算得到教学楼的高度，请借助A小组提供的数据计算教学楼的高度（精确到0.1）（参考数据：sinα＝0.4，cosα＝0.9，tanα＝0.5，sinβ＝0.9，cosβ＝0.3，tanβ＝3）
20．（2025 安徽模拟）中国古代在公元前2世纪就制成了世界上最早的潜望镜，西汉初年成书的《淮南万毕术》中有这样的记载：“取大镜高悬，恳水盆于其下，则见四邻矣”，如图1所示，其工作方法主要利用了光的反射原理．在图2中，AB呈水平状态，AE，CD为法线，∠BCD＝∠ACD＝41°，∠CAE＝37°，AE⊥AB，已知米，求镜面上点C到水盆A的距离．（结果精确到0.1米，参考数据：sin82°≈0.99，cos82°≈0.14，tan82°≈7.12）
2025年中考数学二轮复习考前预测：锐角三角函数
参考答案与试题解析
一．选择题（共10小题）
1．（2025 福建模拟）在Rt△ABC中，∠B＝90°．已知AB＝6，AC＝10，则sinA的值为（　　）
A． B． C． D．
【考点】锐角三角函数的定义．
【专题】等腰三角形与直角三角形；几何直观．
【答案】A
【分析】根据题意画出图形，进而利用锐角三角函数定义求解即可．
【解答】解：如图所示：
∵AB＝6，AC＝10，
∴，
∴，
故选：A．
【点评】本题主要考查了锐角三角函数的定义，正确把握其定义是解题的关键．
2．（2025 福建模拟）我校数学兴趣小组的同学要测量建筑物CD的高度，如图，建筑物CD前有一段坡度为i＝1：2的斜坡BE，小明同学站在斜坡上的B点处，用测角仪测得建筑物屋顶C的仰角为37°，接着小明又向下走了米，刚好到达坡底E处，这时测到建筑物屋顶C的仰角为45°，A、B、C、D、E、F在同一平面内．若测角仪的高度AB＝EF＝1.4米，则建筑物CD的高度约为（　　）（精确到0.1米，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A．38.6 B．39.0 C．40.0 D．41.6
【考点】解直角三角形的应用﹣仰角俯角问题．
【专题】解直角三角形及其应用；运算能力．
【答案】D
【分析】设CD＝x米．延长AB交DE于H，作AM⊥CD于M，FN⊥CD于N，求出BH＝4（米），EH＝8（米），由矩形的性质得出AM＝DH，AH＝DM，FN＝DE，FE＝DN＝1.4（米），在Rt△CFN中，求出CN＝FN＝DE＝（x﹣1.4）（米），AM＝DH＝（8+x﹣1.4）（米），CM＝（x﹣5.6）（米），在Rt△ACM中，由AM＝，得出方程，解方程即可．
【解答】解：如图，延长AB交DE于H，作AM⊥CD于M，FN⊥CD于N，设CD＝x米．
∵BE＝4米，BH：EH＝1：2，
∴BH＝4（米），EH＝8（米），
由题意可得：
∴AM＝DH，AH＝DM，FN＝DE，FE＝DN＝1.4（米），
∵在Rt△CFN中，∠CFN＝45°，
∴CN＝FN＝DE＝（x﹣1.4）（米），
∵AM＝DH＝（8+x﹣1.4）（米），CM＝（x﹣5.6）（米），
∵在Rt△ACM中，∠CAM＝37°，
∴AM＝，
∴8+x﹣1.4≈，
∴x≈41.6（米），
∴CD≈41.6米，
故选：D．
【点评】本题考查解直角三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．
3．（2025 永寿县校级一模）如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，且sin∠BAE＝，若BD＝8，则AE的长为（　　）
A． B．2 C． D．
【考点】解直角三角形；勾股定理；矩形的性质．
【专题】解直角三角形及其应用；运算能力．
【答案】C
【分析】先求得∠ADB＝∠BAE，得到，利用正弦函数的定义求得AB＝4，BE＝2，再利用勾股定理求解即可．
【解答】解：∵AE⊥BD，
∴∠ADB＝90°﹣∠ABE＝∠BAE，
∴，
∴，
∵BD＝8，
∴AB＝4，
∵，
∴，
∴BE＝2，
∴，
故选：C．
【点评】本题考查了解直角三角形的应用．熟练掌握该知识点是关键．
4．（2025 汕头模拟）港珠澳大桥是世界上最长的跨海大桥，被誉为“现代世界七大奇迹”的超级工程，它是我国从桥梁大国走向桥梁强国的里程碑之作．港珠澳大桥主桥为三座大跨度钢结构斜拉桥，其中九洲航道桥主塔造型取自“风帆”，寓意“扬帆起航”，某校九年级学生为了测量该主塔的高度，站在B处看塔顶A，仰角为60°，然后向后走160米（BC＝160米），到达C处，此时看塔顶A，仰角为30°，则该主塔的高度是（　　）
A．80米 B．米 C．160米 D．米
【考点】解直角三角形的应用﹣仰角俯角问题．
【专题】解直角三角形及其应用；运算能力．
【答案】B
【分析】过点A作AD⊥CB，垂足为D，先根据三角形的外角性质可得∠BAC＝∠ACD＝30°，从而可得AB＝BC＝160米，然后在Rt△ABD中，利用锐角三角函数的定义求出AD的长，即可解答．
【解答】解：过点A作AD⊥CB，垂足为D，
∵∠ABD是△ABC的一个外角，∠ABD＝60°，∠ACD＝30°，
∴∠BAC＝∠ABD﹣∠ACD＝30°，
∴∠BAC＝∠ACD＝30°，
∴AB＝BC＝160米，
在Rt△ABD中，AD＝AB sin60°＝160×＝80（米），
∴该主塔的高度是80米，
故选：B．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
5．（2025 登封市一模）如图所示，在矩形网格中，每个小正方形的边长为1，△ABC的三个顶点都在格点上，则tanA的值为（　　）
A． B． C． D．
【考点】解直角三角形．
【专题】解直角三角形及其应用；运算能力．
【答案】B
【分析】在Rt△ABD中，利用锐角三角函数的定义进行计算即可解答．
【解答】解：如图：
在Rt△ABD中，BD＝2，AD＝6，
∴tanA＝＝＝，
故选：B．
【点评】本题考查了解直角三角形，熟练掌握锐角三角函数的定义是解题的关键．
6．（2025 潍坊模拟）在凡尔纳的小说《神秘岛》中，有一段工程师和赫伯特一起测量瞭望塔的高度的情节．工程师先做了一个悬垂，其实就是在绳子的一端栓了一块石头，工程师让赫伯特拿着，然后拿起一根木杆，长度大概为12英尺，两个人一前一后向瞭望塔走去，两个人来到距离瞭望塔485英尺的一个地方，工程师把木杆的一头插到土里，插下去的深度大概是2英尺，接着，工程师从赫伯特手里结果悬垂，对木杆进行校正，知道木杆完全竖直，之后对木杆插到土里的部分进行固定，固定好木杆后，工程师朝着远离木杆的方向走了15英尺，仰面平躺在了地面上（眼睛离木杆15英尺），并且让自己的眼睛能够正好通过木杆的尖端看到瞭望塔的最顶端，工程师在这个点上做了一个标记，如图所示，请你求出此时瞭望塔的高度是（　　）
A．333英尺 B．英尺 C．400英尺 D．英尺
【考点】解直角三角形的应用．
【专题】解直角三角形及其应用；应用意识．
【答案】B
【分析】由题意作图，AB为瞭望塔，DE为木杆，工程师在C点，求出BC，DE的长，再根据三角函数即可求解．
【解答】解：由题意可作图如下：AB为瞭望塔，DE为木杆，工程师在C点，
则有BE＝485英尺，CE＝15英尺，
∴BC＝BE+CE＝500英尺，
∵木杆有2英尺插入了土中，
∴DE＝12﹣2＝10（英尺），
∵AB⊥BC，DE⊥BC，
∴，
则，
解得：，
即瞭望塔高度为英尺，
故选：B．
【点评】本题考查了解直角三角形的应用，熟练掌握锐角三角形函数的定义是解题的关键．
7．（2025 静安区一模）如果锐角A的余弦值为，下列关于锐角A的取值范围的说法中，正确的是（　　）
A．0°＜∠A＜30° B．30°＜∠A＜45°
C．45°＜∠A＜60° D．60°＜∠A＜90°
【考点】特殊角的三角函数值．
【专题】计算题；运算能力．
【答案】C
【分析】根据特殊角的三角函数值判断即可．
【解答】解：∵cos30°＝＞，cos45°＝＞，cos60°＝＜，cosA＝，
∴45°＜∠A＜60°．
故选：C．
【点评】本题考查了特殊角的三角函数值，熟记特殊角的三角函数值是关键．
8．（2025 青浦区一模）如图，点P是航拍飞机在某一高度时的位置，BH是地平线，PH⊥BH，PC∥BH，AB是某大型建筑物的斜面．从点P观测点B的俯角是（　　）
A．∠HPB B．∠CPB C．∠APB D．∠PBA
【考点】解直角三角形的应用﹣仰角俯角问题．
【专题】解直角三角形及其应用；几何直观．
【答案】B
【分析】根据俯角的定义即可得到结论．
【解答】解：∵PC∥BH，BH是地平线，
∴从点P观测点B的俯角是∠CPB，
故选：B．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，熟练掌握俯角的定义是解题的关键．
9．（2025 浦东新区一模）在网格中，每个小正方形的顶点称为格点．如图，在4×4的网格中，点A、B、C都在格点上，那么∠BAC的正切值是（　　）
A． B． C．2 D．
【考点】解直角三角形．
【专题】解直角三角形及其应用；运算能力．
【答案】D
【分析】根据所给网格，连接BC得出BC与AC垂直，再结合正切的定义即可解决问题．
【解答】解：连接BC，如图所示，
则BC⊥AC．
令小正方形网格的边长为a，
则由勾股定理得，
BC＝；
AC＝．
在Rt△ABC中，
tan∠BAC＝．
故选：D．
【点评】本题主要考查了解直角三角形，通过连接BC构造出直角三角形及熟知正切的定义是解题的关键．
10．（2025 奉贤区一模）在测量过程中，常常会遇到仰角和俯角，图中是俯角的角是（　　）
A．∠1 B．∠2 C．∠3 D．∠4
【考点】解直角三角形的应用﹣仰角俯角问题．
【专题】解直角三角形及其应用；几何直观．
【答案】C
【分析】根据俯角的定义，即可解答．
【解答】解：在测量过程中，常常会遇到仰角和俯角，图中是俯角的角是∠3，
故选：C．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，熟练掌握俯角的定义是解题的关键．
二．填空题（共5小题）
11．（2025 松江区一模）已知一个斜坡的坡度i＝1：1，那么该斜坡的坡角为 　45　度．
【考点】解直角三角形的应用﹣坡度坡角问题．
【专题】解直角三角形及其应用；应用意识．
【答案】45．
【分析】坡度＝坡角的正切值，据此直接解答．
【解答】解：∵tanα＝1：1＝1，
∴坡角＝45°．
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题，把坡面与水平面的夹角α叫做坡角，坡度i与坡角α之间的关系为：i＝h/l＝tanα．
12．（2025 静安区一模）如图，已知△ABC的三个顶点均在小正方形的方格顶点上，那么sinC的值是 　　．
【考点】解直角三角形．
【专题】解直角三角形及其应用；运算能力．
【答案】．
【分析】过点A作BC的垂线，结合面积法及正弦的定义即可解决问题．
【解答】解：过点A作BC的垂线，垂足为M，
令小正方形网格的边长为a，
则由勾股定理得，
BC＝，
AC＝．
由面积法可知，
，
所以AM＝．
在Rt△ACM中，
sinC＝．
故答案为：．
【点评】本题主要考查了解直角三角形，巧用面积法就熟知正弦的定义是解题的关键．
13．（2025 静安区一模）如图，在△ABC中，BD是△ABC的中线，BC＝2BD，AC＝6，那么AB的长为 　8　．
【考点】解直角三角形．
【专题】解直角三角形及其应用；几何直观；运算能力．
【答案】8．
【分析】过点D作DE⊥AB于点E，过点C作CF⊥AB交AB的延长线于F，解直角三角形求出DE＝3，AE＝6，证明DE是△ACF的中位线得CF＝2DE＝6，AE＝EF＝6，设BE＝a，则BF＝EF﹣BE＝6﹣a，AB＝AE+BE＝6+a，在Rt△BDE和Rt△CBF中，利用勾股定理构造方程求出a＝2，进而可得AB的长．
【解答】解：过点D作DE⊥AB于点E，过点C作CF⊥AB交AB的延长线于F，如图所示：
∵BD是△ABC的中线，AC＝，
∴AD＝CD＝AC＝，
在Rt△ADE中，tanA＝＝，
∴AE＝2DE，
由勾股定理得：AD＝＝，
∴，
∴DE＝3，
∴AE＝2DE＝6，
∵DE⊥AB，CF⊥AB，
∴DE∥CF，
又∵BD是△ABC的中线，
∴DE是△ACF的中位线，
∴CF＝2DE＝6，AE＝EF＝6，
设BE＝a，则BF＝EF﹣BE＝6﹣a，AB＝AE+BE＝6+a，
在Rt△BDE中，由勾股定理得：BD2＝DE2+BE2＝32+a2，
在Rt△CBF中，由勾股定理得：BC2＝BF2+CF2＝（6﹣a）2+62，
∴BC＝2BD，
∴4（32+a2）＝（6﹣a）2+62，
整理得：a2+4a﹣12＝0，
解得：a＝2，a＝﹣6（不合题意，舍去），
∴AB＝6+a＝8．
故答案为：8．
【点评】此题主要考查了解直角三角形，正确地添加辅助线构造直角三角形，灵活运用锐角三角函数的定义及勾股定理进行运算是解决问题的关键．
14．（2025 徐汇区一模）如图，热气球探测器显示，从热气球A处测得一栋楼顶部C处的仰角是37°，测得这栋楼的底部B处的俯角是60°，热气球与这栋楼的水平距离是30米，那么这栋楼的高度是 　73.5　米（精确到0.1米）．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，）
【考点】解直角三角形的应用﹣仰角俯角问题．
【专题】解直角三角形及其应用；应用意识．
【答案】73.5．
【分析】过点A作AD⊥BC于点D，则AD＝30米，在Rt△ADB中和Rt△ACD中，根据锐角三角函数中的正切可以分别求得BD和CD的长，从而可以求得BC的长，本题得以解决．
【解答】解：过点A作AD⊥BC于点D，
由题意可得，∠CAD＝37°，∠BAD＝60°，AD＝30米，∠ADC＝∠ADB＝90°，
在Rt△ADC中，tan∠CAD＝，
∴CD＝AD tan37°≈30×0.75＝22.5（米），
在Rt△ADB中，tan∠BAD＝，
∴BD＝AD tan60°＝30×＝30，
∴BC＝BD+CD＝22.5+30≈73.5（米），
即这栋楼的高度BC是73.5米．
故答案为：73.5．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题、锐角三角函数，解答此类问题的关键是明确题意，利用锐角三角函数解答．
15．（2025 青浦区一模）如图，梯形ABCD是某水库大坝的横截面．已知坝高AE＝8m，如果将坡度为1：的斜坡AB改为坡度为1：2的斜坡AP，那么大坝底部应加宽 　（16﹣8）　m．（结果保留根号）
【考点】解直角三角形的应用﹣坡度坡角问题．
【专题】解直角三角形及其应用；应用意识．
【答案】（16﹣8）．
【分析】根据垂直的定义得到∠AEB＝90°，根据三角函数的定义得到BE＝8，PE＝16，于是得到PB＝PE﹣BE＝（16﹣8）m．
【解答】解：∵AE⊥BC，
∴∠AEB＝90°，
∵AE＝8m，
∴tan∠ABE＝＝，
∴BE＝＝＝8，
∵tanP＝＝，
∴＝，
∴PE＝16，
∴PB＝PE﹣BE＝（16﹣8）m，
答：大坝底部应加宽（16﹣8）m．
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题，熟练掌握三角函数的定义是解题的关键．
三．解答题（共5小题）
16．（2025 鼓楼区校级模拟）物流中心A与三个菜鸟驿站B、C、D的平面示意图如图．D在A的正南方，C在A的东南方向上且在D的北偏东30°方向上，B在A的正东方且∠ABC＝37°，已知AB＝5.6km．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，≈1.73）．
（1）求驿站B、C之间的距离；
（2）派送员小外计划9：00从A出发沿着A→B→C→D的路线派送快递到三个驿站，上午9：50完成快递派送．但导航显示AB路段拥堵严重，于是他改变路线（9：00出发），沿着A→D→C→B的路线派送快递到三个驿站．若AD路段行驶的平均速度为40km/h，其余路段的平均行驶速度为30km/h且小外在每个驿站均停留7min存放快递．请通过计算说明他能否在9：50之前完成派送．
【考点】解直角三角形的应用﹣方向角问题．
【专题】解直角三角形及其应用；运算能力．
【答案】（1）4km；
（2）他能在9：50之前完成派送．
【分析】（1）过点C作CE⊥AB于点E，设AE＝x，则EB＝AB﹣AE＝5.6﹣x，根据∠EAC＝45°，∠EBC＝37°，得出EC＝tan45° AE＝x，EC＝EB tan37°≈0.75（5.6﹣x），进而建立方程，解方程得出x＝2.4，在Rt△EBC中，根据BC＝即可求解；
（2）过点C作CF⊥AD于点F，求得 AD＝AF+FD＝2.4+4.2＝6.6，进而可得AD所需时间，分别求得DC，BC所需时间，加上每个驿站均停留的时间，与50分钟比较大小，即可求解．
【解答】解：（1）过点C作CE⊥AB于E，
设AE＝x，
∴BE＝AB﹣AE＝（5.6﹣x）km，
在Rt△ACE中，∠CAE＝45°，
∴∠ACE＝45°＝∠CAE，
∴CE＝AE＝x，
在Rt△BCE中，∠B＝37°，
tan37°＝，
∴≈0.75，
解得x＝2.4，
∴CE＝2.4，
∴BC＝≈＝4（km）．
答：驿站B、C之间的距离约为4km；
（2）解：如图所示，过点C作CF⊥AD于点F，
∴四边形AECF是矩形，
又∵AE＝EC，
∴四边形AECF是正方形，
∴AF＝FC＝EC＝2.4，
∵∠D＝30°，
∴DC＝2FC＝4.8，，
∵AD路段行驶的平均速度为40km/h，
∴所需时间为小时，
其余路段的平均行驶速度为30km/h，
∴D→C→B所需时间为小时，
所以总共用时为：小时，
×60＝48.5分钟＜50分钟，
∴他能在9：50之前完成派送．
【点评】本题考查了解直角三角形的应用；正确理解题意和熟练掌握相关知识是解题的关键．
17．（2025 雁塔区校级模拟）随着农业现代化的进一步推进，新农村的积极建设，农民伯伯可用无人机进行药物喷洒来消灭虫害．如图，这是一位农民伯伯喷药过程中的实时画面示意图，他在水平地面上点A处测得无人机的位置点D的仰角为53°．当他迎着坡度为8：15的斜坡从点A走到点B时，无人机恰好从点D沿着水平方向飞到点C此时，他在点B处测得点C的仰角∠CBE为45°．已知AB＝34米，CD＝50米，这位农民伯伯让无人机沿与水平地面平行的方向飞行以便喷洒均匀．点A，B，C，D，E，F在同一竖直平面内，求此时无人机的位置点C距水平地面AF的高度．（测角仪的高度忽略不计．参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈）
【考点】解直角三角形的应用﹣仰角俯角问题；解直角三角形的应用﹣坡度坡角问题．
【专题】解直角三角形及其应用；运算能力．
【答案】此时无人机的位置点C距水平地面AF的高度约为144米．
【分析】过点B作BH⊥AF，垂足为H，过点D作DG⊥AF，垂足为G，过点C作CN⊥AF，垂足为N，交BE于点M，根据题意可得：BH＝MN，DG＝CN，BM＝HN，CD＝GN＝50米，再根据已知可设BH＝8x米，则AH＝15x米，从而在Rt△ABH中，利用勾股定理进行计算可求出BH和AH的长，然后设HG＝y米，则BM＝HN＝（x+50）米，AG＝（30+x）米，分别在Rt△ADG和Rt△BMC中，利用锐角三角函数的定义求出DG和CM的长，从而利用线段的和差关系列出关于y的方程，进行计算即可解答．
【解答】解：过点B作BH⊥AF，垂足为H，过点D作DG⊥AF，垂足为G，过点C作CN⊥AF，垂足为N，交BE于点M，
由题意得：BH＝MN，DG＝CN，BM＝HN，CD＝GN＝50米，
∵斜坡AB的坡度为8：15，
∴＝，
∴设BH＝8x米，则AH＝15x米，
在Rt△ABH中，AB＝＝＝17x（米），
∵AB＝34米，
∴17x＝34，
解得：x＝2，
∴BH＝MN＝16米，AH＝30米，
设HG＝y米，
∴BM＝HN＝HG+GN＝（x+50）米，AG＝AH+HG＝（30+x）米，
在Rt△ADG中，∠DAG＝53°，
∴DG＝AG tan53°≈（x+30）米，
在Rt△BMC中，∠CBM＝45°，
∴CM＝BM tan45°＝（x+50）米，
∵DG＝CN，
∴DG＝CM+MN，
∴（x+30）＝x+50+16，
解得：x＝78，
∴CN＝x+50+16＝144（米），
∴此时无人机的位置点C距水平地面AF的高度约为144米．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，坡度坡角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
18．（2025 雁塔区校级一模）小新的数学研学日记
课题：测量旗杆的高度
地点：操场
时间：2025月1月13日
昨天，晴．高老师要带我们去操场测量旗杆的高度，我们小组设计方案：小卓拿着标杆垂直于地面放置，我和小越用卷尺测量标杆、标杆的影长和旗杆的影长，如图1所示，标杆AB＝a，影长BC＝b，旗杆的影长DF＝c，则可求得旗杆DE的高度为 　　．
今天，阴．设计方案：如图2所示，高老师将升旗用绳子拉直，使绳子的底端G刚好触到地面，用仪器测得绳子与地面的夹角为37°，然后又将绳子拉到一个0.3米高的平台上，拉直绳子使绳子上的H点刚好触到平台时剩余的绳子长度为5米，此时测得绳子与平台的夹角为54°，利用这些数据能求出旗杆DE的高度吗？
请你回答小新的问题．若能，请求出旗杆的高度；若不能，请说明理由．
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，sin54°≈0.8，cos54°≈0.58，tan54°≈1.45）
【考点】解直角三角形的应用﹣仰角俯角问题；相似三角形的应用．
【专题】解直角三角形及其应用；应用意识．
【答案】，11.1米．
【分析】证明△ABC∽△EDF，根据相似三角形的性质列出比例式，把已知数据代入计算求出DE；过点H作HQ⊥DE于Q，HP⊥GD于P，根据正弦的定义求出DE．
【解答】解：∵AB∥DE，
∴△ABC∽△EDF，
∴＝，即＝，
解得：DE＝，
过点H作HQ⊥DE于Q，HP⊥GD于P，
则QD＝HP＝0.3米，
∴EQ＝（ED﹣0.3）米，
由题意可知：EH＝EG﹣5，
在Rt△EQH中，∠EHQ＝54°，
则sin∠EHQ＝，
∴EQ＝EH sin∠EHQ，
∴ED﹣0.3≈0.8（EG﹣5），
在Rt△EDQ中，∠EGD＝37°，
则sin∠EGD＝，
∴ED＝EG sin∠EGD，
∴ED≈0.6EG，
则，
解得：，
∴旗杆的高度约为11.1米．
故答案为：．
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题、相似三角形的应用，熟记锐角三角函数的定义是解题的关键．
19．（2025 济南模拟）如图，某校教学楼后面紧邻着一个山坡，山坡面是一块平地，BC∥AD，BE⊥AD，斜坡AB长26m，斜坡AB的坡比为2.4：1．
（1）求坡高BE；
（2）本学期初三学生开展数学学科“综合与实践”活动，主题：测量高度A小组选择测量教学楼高度，他们的做法是：在教学楼F处安置测倾器，测得此时B的仰角∠BFG＝α和A的俯角∠AFG＝β，然后借助已知中的数据计算得到教学楼的高度，请借助A小组提供的数据计算教学楼的高度（精确到0.1）（参考数据：sinα＝0.4，cosα＝0.9，tanα＝0.5，sinβ＝0.9，cosβ＝0.3，tanβ＝3）
【考点】解直角三角形的应用．
【专题】等腰三角形与直角三角形；推理能力．
【答案】（1）BE＝24m；
（2）教学楼的高度为16.3m．
【分析】（1）由斜坡AB的坡比可设设BE＝12x m，AE＝5x m，在Rt△ABE中，根据勾股定理构造方程即可求解；
（2）设BG＝x m，则EG＝24﹣x（m），由得到FG＝2x m，证明四边形FHEG为矩形，得到FG＝HE＝2x m，FH＝GE＝24﹣x（m），FG∥HE，进而∠β＝∠4，AH＝2x﹣10（m），根据，即可求出方程，求解即可．
【解答】解：（1）∵斜坡AB长26m，斜坡AB的坡比为2.4：1，
∴＝＝，
设BE＝12x m，AE＝5x m，
∵在Rt△ABE中，AE2+BE2＝AB2，
∴（5x）2+（12x）2＝262，解得x＝2，
∴AE＝10m，BE＝24m；
（2）由（1）知，BE＝24m，
设BG＝x m，则EG＝24﹣x（m），
∵，
∴FG＝2x m，
∵FG⊥BE，BE⊥HD，FH⊥HD，
∴∠1＝∠2＝∠3＝90°，
∴四边形FHEG为矩形，
∴FG＝HE＝2x m，FH＝GE＝24﹣x（m），FG∥HE，
∴∠β＝∠4，AH＝HE﹣AE＝2x﹣10（m），
∴，
即，
解得：，
经检验，是该分式方程的解．
∴FH＝24﹣7.71＝16.29≈16.3（米），
故教学楼的高度为16.3米．
【点评】本题考查的是解直角三角形的应用，熟知锐角三角函数的定义及勾股定理是解题的关键．
20．（2025 安徽模拟）中国古代在公元前2世纪就制成了世界上最早的潜望镜，西汉初年成书的《淮南万毕术》中有这样的记载：“取大镜高悬，恳水盆于其下，则见四邻矣”，如图1所示，其工作方法主要利用了光的反射原理．在图2中，AB呈水平状态，AE，CD为法线，∠BCD＝∠ACD＝41°，∠CAE＝37°，AE⊥AB，已知米，求镜面上点C到水盆A的距离．（结果精确到0.1米，参考数据：sin82°≈0.99，cos82°≈0.14，tan82°≈7.12）
【考点】解直角三角形的应用．
【专题】解直角三角形及其应用；应用意识．
【答案】镜面上点C到水盆A的距离约为11.1米．
【分析】过点A作AF⊥BC，由∠BCD＝∠ACD＝41°可得∠ACB＝82°，由EA⊥AB，∠CAE＝37°可得∠CAB＝53°，进而得到∠ABC＝45°，分别解Rt△ABF和Rt△ACF即可求解．
【解答】解：过点A作AF⊥BC，垂足为F，则∠AFB＝∠AFC＝90°，
∵EA⊥AB，
∴∠EAB＝90°，
∵∠BCD＝∠ACD＝41°，
∴∠ACB＝82°，
∵∠CAE＝37°，
∴∠CAB＝∠EAB﹣∠EAC＝53°，
∴∠ABC＝180°﹣∠CAB﹣∠ACB＝45°，
在Rt△ABF中，∠ABC＝45°，
∴（米），
在Rt△ACF中，∠ACB＝82°，
∴AC＝AF÷sin82°≈11÷0.99≈11.1（米），
∴镜面上点C到水盆A的距离约为11.1米．
【点评】本题考查了解直角三角形的应用，掌握解直角三角形是解题的关键．
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑