 资源简介
资源简介
中小学教育资源及组卷应用平台
人教版2024—2025学年七年级下学期数学第三次月考全真模拟试卷满分:120分 时间:120分钟 范围:第七章到第十一章
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四组图形中,不能视为由一个基本图形通过平移得到的是( )
A. B. C. D.
2.若a>b,则下列式子正确的是( )
A.﹣3+a<﹣3+b B.ac>bc
C.a2>b2 D.
3.下列实数中,无理数是( )
A. B. C.0 D.
4.如图,点P是直线l外一点,A、B、C、D都在直线l上,PB⊥l于B,在P与A、B、C、D四点的连线中,线段PB最短,依据是( )
A.两点确定一条直线
B.两点之间,线段最短
C.过一点有且只有一条直线与已知直线垂直
D.垂线段最短
5.估计的值在( )
A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间
6.下列命题中是假命题的是( )
A.如果a∥b,b∥c,那么a∥c
B.三角形中最大的角一定大于或等于60°
C.两条直线被第三条直线所截,内错角相等
D.对顶角相等
7.如图①,“二八大杠”传统老式自行车承载了一代人的回忆,图②是它的几何示意图.已知BC∥DE,AB∥CD,当∠ABD=70°,∠DBC=45°,∠CDE的度数为( )
A.25° B.35° C.65° D.115°
8.《九章算术》中的“盈不足”一章有一道题,原文是:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何.”意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3解(斛,是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶可以盛酒x斛,1个小桶可以盛酒y斛,则可列方程组( )
A. B.
C. D.
9.若不等式组无解,则k的取值范围为( )
A.k>2 B.k≥2 C.k<﹣2 D.k≤﹣2
10.已知点A(2m﹣9,m﹣3),且点A到两坐标轴的距离相等,则点A的坐标为( )
A.(3,﹣3)和(﹣1,1) B.(3,﹣3)和(1,﹣1)
C.(3,3)和(﹣1,1) D.(3,3)和(﹣1,﹣1)
二、填空题(每小题3分,满分18分)
11.已知,则的值约为 .
12.如图,实数a,b,c在数轴上对应点的位置如图所示,化简|b﹣a||b﹣c|的结果是 .
13.如图,将三角形ABC向右平移得到三角形DEF,且点B,E,C,F在同一条直线上,若EC=3,BF=13,则AD的长为 .
14.如果是方程2x﹣3y=2025的一组解,那么代数式2024﹣2m+3n= .
15.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=62°,则∠AEG= °.
16.若关于x,y的方程组的解使4x+7y>2,则k的取值范围是 .
人教版2024—2025学年七年级下学期数学第三次月考全真模拟试卷考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组:.
18.解下列方程组:
(1);
(2).
19.已知正数m的两个平方根分别为3a﹣3和1﹣2a.
(1)求a的值;
(2)求的值.
20.(1)计算:;
(2)求等式中x的值:(x﹣1)2=16.
21.某商店决定购进甲、乙两种文创产品.若购进甲种文创产品7件,乙种文创产品3件,则费用是285元;若购进甲种文创产品2件,乙种文创产品6件,则费用是210元.
(1)求购进的甲、乙两种文创产品每件的费用各是多少元?
(2)若该商店决定购进这两种文创产品共200件,考虑市场需求和资金周转,用于购买这200件文创产品的总费用不少于5350元,且不超过5368元,求该商店共有几种购进这两种文创产品的方案.
22.在平面直角坐标系中,已知点A(a,0),B(b,6),C(c,3),a,b,c满足.
(1)若a=2,求三角形ABC的面积;
(2)若三角形ABC的面积等于12,求a的值.
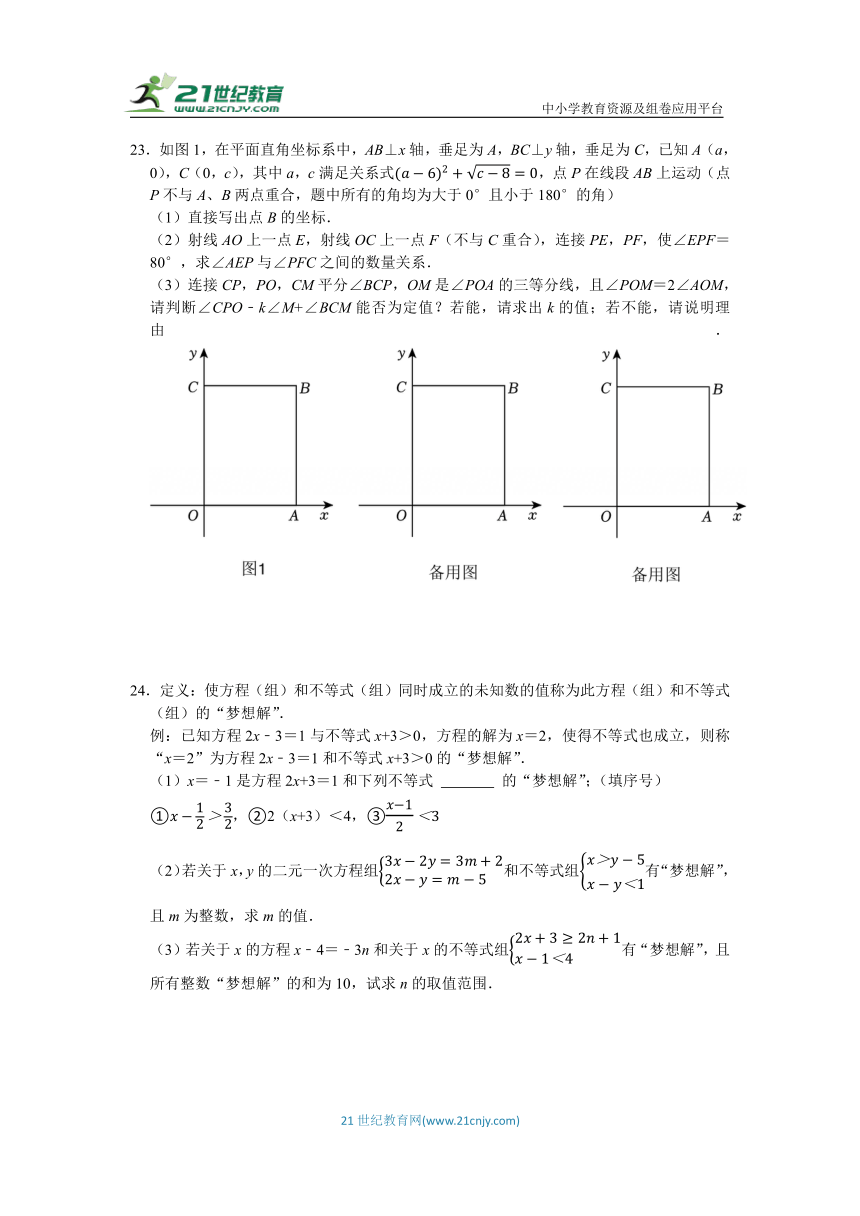
23.如图1,在平面直角坐标系中,AB⊥x轴,垂足为A,BC⊥y轴,垂足为C,已知A(a,0),C(0,c),其中a,c满足关系式,点P在线段AB上运动(点P不与A、B两点重合,题中所有的角均为大于0°且小于180°的角)
(1)直接写出点B的坐标.
(2)射线AO上一点E,射线OC上一点F(不与C重合),连接PE,PF,使∠EPF=80°,求∠AEP与∠PFC之间的数量关系.
(3)连接CP,PO,CM平分∠BCP,OM是∠POA的三等分线,且∠POM=2∠AOM,请判断∠CPO﹣k∠M+∠BCM能否为定值?若能,请求出k的值;若不能,请说明理由.
24.定义:使方程(组)和不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“梦想解”.
例:已知方程2x﹣3=1与不等式x+3>0,方程的解为x=2,使得不等式也成立,则称“x=2”为方程2x﹣3=1和不等式x+3>0的“梦想解”.
(1)x=﹣1是方程2x+3=1和下列不等式 的“梦想解”;(填序号)
①,②2(x+3)<4,③
(2)若关于x,y的二元一次方程组和不等式组有“梦想解”,且m为整数,求m的值.
(3)若关于x的方程x﹣4=﹣3n和关于x的不等式组有“梦想解”,且所有整数“梦想解”的和为10,试求n的取值范围.
25.已知A、B两点的坐标分别为A(﹣2,1),B(﹣4,﹣1),将线段AB水平向右平移了6个单位长度到DC,连接AD,BC,得四边形ABCD.
(1)点C的坐标为 ,点D的坐标为 ;
(2)如图1,E为x轴上一点,若DE平分∠ADC,且DE⊥HC于E,,求∠BHC与∠ABH的数量关系;
(3)如图2,直线CG⊥x轴于G,直线CG上有一动点Q,连接BQ、DQ,求BQ+DQ最小时Q点的坐标,并说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D B C C B B C
1.【解答】解:由图可知,A、B、D可以由平移得到,C由轴对称得到.
故选:C.
2.【解答】解:A.若a>b,则﹣3+a>﹣3+b,故选项A错误;
B.若a>b,当c=0时,ac=bc;当c>0时,ac>bc;当c<0时,ac<bc,故选项B错误;
C.若a>b,若a=﹣2,b=﹣3,满足a>b,但a2=4,b2=9,a2<b2,故选项C错误;
D.∵m2+1>0恒成立,若a>b,则,故选项D正确.
故选:D.
3.【解答】解:A.∵,是无理数,∴此选项符合题意;
B.∵是有理数,∴此选项不符合题意;
C.∵0是有理数,∴此选项不符合题意;
D.∵,是有理数,∴此选项不符合题意;
故选:A.
4.【解答】解:PB⊥l于B,在P与A、B、C、D四点的连线中,线段PB最短,依据是垂线段最短.
故选:D.
5.【解答】解:∵,
∴45,
∴23.
故选:B.
6.【解答】解:A、如果a∥b,b∥c,那么a∥c,是真命题;
B、三角形中最大的角一定大于或等于60°,是真命题;
C、两条直线被第三条直线所截,若这两条直线平行,则内错角相等,故原命题是假命题;
D、对顶角相等,是真命题;
故选:C.
7.【解答】解:∵AB∥CD,
∴∠BDC=∠ABD=70°,
∵BC∥DE,
∴∠DBC+∠BDE=180°,
∴∠BDE=180°﹣∠DBC=180°﹣45°=135°,
∴∠CDE=∠BDE﹣∠BDC=135°﹣70°=65°.
故选:C.
8.【解答】解:设1个大桶可以盛酒x斛,1个小桶可以盛酒y斛,则列方程组是
,
故选:B.
9.【解答】解:,得:,
由条件可知k>0,,,
令,
由条件可知:反比例函数的图象在第四象限,y随着k的增大而增大,
当y=﹣3时,k=2,
∴当时,k≥2;
故选:B.
10.【解答】解:由题意得|2m﹣9|=|m﹣3|,
∴2m﹣9=m﹣3或2m﹣9=﹣(m﹣3),
解得m=6,或m=4,
当m=6时,2m﹣9=2×6﹣9=3,m﹣3=3,
∴点A的坐标为(3,3),
当m=4时,2m﹣9=2×4﹣9=﹣1,m﹣3=4﹣3=1,
∴点A的坐标为(﹣1,1),
综上所述,点A的坐标为(3,3)或(﹣1,1).
故选:C.
二、填空题
11.【解答】解:把0.0023向右移动4位,即可得到23,
显然只需对4.80向左移动2位得到0.048.
故答案为:0.048.
12.【解答】解:由数轴可得:a<0,b﹣a>0,b﹣c<0,
故原式=﹣a+b﹣a﹣(a+b)﹣[﹣(b﹣c)]
=﹣a+b﹣a﹣a﹣b+b﹣c
=﹣3a+b﹣c.
故答案为:﹣3a+b﹣c.
13.【解答】解:∵△ABC向右平移得到△DEF,且点B,E,C,F在同一条直线上,
∴AD=BE=CF,
∵EC=3,BF=13,
∴AD5.
故答案为:5.
14.【解答】解:把代入方程2x﹣3y=2025得:2m﹣3n=2025,
∴﹣2m+3n=﹣2025,
∴2024﹣2m+3n
=2024﹣2025
=﹣1,
故答案为:﹣1.
15.【解答】解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠1=62°,
∵沿EF折叠D到D′,
∴∠FEG=∠DEF=62°,
∴∠AEG=180°﹣62°﹣62°=56°,
故答案为:56.
16.【解答】解:
由①×2﹣②×3,并解得
y;③
由①×3+②×2,得
13x=3k+1,解得
x;④
把③④代入4x+7y>2,得
472,
不等式的两边同时除以2,得
271,
不等式是两边同时乘以13,得
2×(3k+1)+7×(k﹣4)>13,
去括号,得
13k﹣26>13,
移项,得
13k>39,
不等式的两边同时除以13,得
k>3;
故答案为:k>3.
或①×2﹣②得到:4x+7y=2k﹣4,
由题意2k﹣4>2,
∴k>3.
三、解答题
17.【解答】解:,
解①得x<2.5;
解②得x≥﹣1;
所以,原不等式组的解集为﹣1≤x<2.5.
18.【解答】解:(1)①+②得:x=2,
把x=2代入②得:,
∴方程组的解为:;
(2)方程组化简为:,
①+②得:x=5,
把x=5代入①得:y=1,
∴方程组的解为:.
19.【解答】解:(1)∵正数m的两个平方根分别为3a﹣3和1﹣2a,
∴3a﹣3+1﹣2a=0,
a﹣2=0,
a=2;
(2)由(1)得:a=2,
∴m=(3a﹣3)2=(3×2﹣3)2=9,
∴
=﹣2.
20.【解答】解:(1)
=22﹣2
;
(2)开平方,得x﹣1=±4,
解得x=5或x=﹣3.
21.【解答】解:(1)设甲种文创产品每件的费用是x元,乙种文创产品每件的费用是y元,
根据题意得:,
解得:,
答:甲种文创产品每件的费用是30元,乙种文创产品每件的费用是25元;
(2)设购进甲种文创产品m件,则购进乙种文创产品(200﹣m)件,
由题意得:,
解得:70≤m≤73.6,
∵m为正整数,∴m=70,71,72,73,
∴该商店共有4种购进这两种文创产品的方案.
22.【解答】解:(1)将a=2代入,
得,
解得,
∴A(2,0),B(2,6),C(0,3).
如图,连接AB、AC、BC.
过点C作CD⊥AB于点D,则D(2,3).
∵AB=6,CD=2,
∴S△ABCAB CD6×2=6,
∴若a=2,三角形ABC的面积为6.
(2),
①+②,得3(a﹣b)=0,解得b=a,
b=a代入①,得c(a﹣2).
∴A(a,0),B(a,6),C((a﹣2),3).
如图,连接AB、AC、BC.
过点C作CE⊥AB于点E,则E(a,3).
∵AB=6,CE=|a(a﹣2)|=|a+1|,
∴S△ABCAB CE6|a+1|=12,
∴a=6或﹣10,
∴a的值为6或﹣10.
23.【解答】(1)解:∵,
∴a﹣6=0,c﹣8=0,
∴a=6,c=8,
∴A(6,0),C(0,8),
∵AB⊥x轴,BC⊥y轴,
∴点B的坐标为(6,8);
(2)解:∵AB⊥x轴,BC⊥y轴,
∴∠OAB=∠BCO=∠AOC=90°,
∴四边形OABC为长方形,
∴∠B=∠BCO=∠PAE=90°,
①当点E、F分别在线段OA、OC上时,
如图,∠PAE=90°,
∴∠APE=90°﹣∠AEP,
∵∠EPF=80°,
∴∠BPF=180°﹣∠EPF﹣∠APE=180°﹣80°﹣(90°﹣∠AEP)=∠AEP+10°,
∵∠B+∠BCF+∠PFC+∠BPF=360°,
∴90°+90°+∠PFC+∠AEP+10°=360°,
即∠PFC+∠AEP=170°;
②当点E在AO的延长线上,点F在线段OC的延长线上时,如图,
∵∠PAE=90°,
∴∠APE=90°﹣∠AEP,
∵∠EPF=80°,
∴∠APF=80°+∠APE=80°+(90°﹣∠AEP)=170°﹣∠AEP,
∴∠BPF=180°﹣∠APF=180°﹣(170°﹣∠AEP)=10°+∠AEP,
∵四边形OABC为长方形,∴AB∥OF,∴∠PFC=∠BPF,
∴∠PFC=∠AEP+10°,即∠PFC﹣∠AEP=10°;③当点E在线段OA上,点F在OC的延长线上时,如图,
∵∠PAE=90°,
∴∠APE=90°﹣∠AEP,
∵∠EPF=80°,
∴∠BPF=180°﹣∠EPF﹣∠APE=180°﹣80°﹣(90°﹣∠AEP)=∠AEP+10°,
∵四边形OABC为长方形,
∴AB∥OF,
∴∠PFC=∠BPF,
∴∠PFC=∠AEP+10°,即∠PFC﹣∠AEP=10°,
综上,∠AEP与∠PFC之间的数连关系为:∠PFC+∠AEP=170°或∠PFC﹣∠AEP=10°;
(3)解:∠CPO﹣k∠M+∠BCM能为定值,理由如下:
∵CM平分∠BCP,OM是∠POA的三等分线,
∴∠BCP=2∠BCM,∠AOP=3∠AOM,
过点P作PH∥OA,
∵OA∥BC,
∴PH∥BC,
∴∠CPH=∠BCP=2∠BCM,∠OPH=∠AOP=3∠AOM,
∴∠CPO=∠CPH+∠OPH=2∠BCM+3∠AOM,
同理可得∠M=∠BCM+∠AOM,
∴∠CPO﹣k∠M+∠BCM=2∠BCM+3∠AOM﹣k∠M+∠BCM
=3(∠BCM+∠AOM)﹣k∠M
=3∠M﹣k∠M,=(3﹣k)∠M,
∴当3﹣k=0,即k=3时,∠CPO﹣k∠M+∠BCM为定值0.
24.【解答】解:(1)解①得:x>2,故方程2x+3=1不是①的“梦想解”;
解②得:x<﹣1,故方程2x+3=1不是②“梦想解”;
解③得:x<7,故方程2x+3=1是③的“梦想解”;
故答案为:③
(2)解方程组
得:,
∴x﹣y=2m+7,
∵解是不等式组的“梦想解”,
∴﹣5<2m+7<1,
∴﹣6<m<﹣3,
∵m为整数,
∴m为﹣5或﹣4;
(3)解方程x﹣4=﹣3n得:x=4﹣3n,
解不等式组得:n﹣1≤x<5,
∴4﹣3n≥n﹣1,
∴n,
∴x=4﹣3n,
∵所有整数“梦想解”的和为10,
∴整数“梦想解”为1,2,3,4,
∵关于x的方程x﹣4=﹣3n和关于x的不等式组有“梦想解”,
∴1<4﹣3n≤4,
解得0≤n<1.
25.【解答】解:(1)∵A、B两点的坐标分别为A(﹣2,1),B(﹣4,﹣1),将线段AB水平向右平移了6个单位长度到DC,
∴C(2,﹣1),D(4,1),
故答案为:(2,﹣1),(4,1);
(2)将线段AB水平向右平移了6个单位长度到DC,设CH交AD于F,BH交AD于P,
∴AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AD∥BC,
∴∠DFC=∠HCB,
∵DE平分∠ADC,且DE⊥HC于E,,
∴∠ABC=∠ADC=4∠ABH,
∴∠HBC=∠ABC﹣∠ABH=3∠HBA,
∵DE平分∠ADC,DE⊥HC,
∴DC=DF,
∴,
∴∠HCB=90°﹣2∠ABH,
∴∠BHC=180°﹣∠HBC﹣∠HCB=180°﹣3∠HBA﹣(90°﹣2∠ABH)=90°﹣∠ABH;
(3)BQ+DQ最小时Q点的坐标为,理由如下:
连接BD交CG于Q′,如图2,
由两点间线段最短可知,当B、D、Q三点共线时BQ+DQ最小,
即Q在Q′位置时BQ+DQ最小,
∵直线CG⊥x轴于G,
∴G的横坐标2,
设Q点坐标为(2,m),S△BCD=S△BCQ′+S△DCQ′,
∴,
解得,
,
∴,
即BQ+DQ最小时Q点的坐标为.
21世纪教育网(www.21cnjy.com)
展开更多......
收起↑
 资源预览
资源预览




 资源预览
资源预览




