资源简介

中小学教育资源及组卷应用平台
苏科版2024—2025学年七年级下册数学期末考试全真模拟试卷
考生注意：本试卷共三道大题，25道小题，满分120分，时量120分钟
第I卷
一、选择题（每题只有一个正确选项，每小题3分，满分30分）
1．节约资源，保护环境，人人有责．下列垃圾分类指引标志图形中，既是轴对称又是中心对称图形的是（　　）
A． B． C．D．
2．若2a＝5，2b＝3，则2a﹣b的值为（　　）
A． B．2 C．4 D．15
3．若（y﹣3）（y+2）＝y2+my+n，则m，n的值分别为（　　）
A．m＝1，n＝﹣6 B．m＝﹣1，n＝﹣6 C．m＝5，n＝6 D．m＝﹣5，n＝6
4．若（m+1）x|m|+2＞0是关于x的一元一次不等式，则该不等式的解集为（　　）
A．x＝0 B．x＜﹣3 C．x＞﹣1 D．x＜﹣1
5．若实数a，b满足a2+b2＝8，ab＝4，则a+b的值为（　　）
A． B．4 C． D．±4
6．我国明代《算法统宗》一书中有这样一题：“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托（一托按照5尺计算）．”大意是：现有一根竿和一条绳索，如果用绳索去量竿，绳索比竿长5尺；如果将绳索对折后再去量竿，就比竿短5尺，则绳索长几尺？设竿长x尺，绳索长y尺，根据题意可列方程组为（　　）
A． B．
C． D．
7．计算（﹣2）100+（﹣2）99的结果为（　　）
A．﹣299 B．299 C．﹣2 D．2
8．校团委开展以“我爱读书”为主题的演讲比赛活动，为奖励表现突出的学生，计划拿出200元钱全部用于购买单价分别为8元和10元的两种笔记本（两种都要购买）作为奖品，则购买方案有（　　）
A．5种 B．4种 C．3种 D．2种
9．如图，用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形，则每个小长方形的周长是（　　）
A．60厘米 B．80厘米 C．100厘米 D．120厘米
10．已知a＝2023x+2022，b＝2023x+2023，c＝2023x+2024，则a2+b2+c2﹣ab﹣ac﹣bc的值是（　　）
A．0 B．1 C．2 D．3
二、填空题（6小题，每题3分，共18分）
11．俗话说：“水滴石穿”，水滴不断地落在一块石头的同一个位置，经过几年后，石头上形成了一个深度为0.0039毫米的小洞，数据0.0039用科学记数法表示为 　 　 ．
12．是关于x，y的二元一次方程mx+y＝6的解，则m的值为 　 　 ．
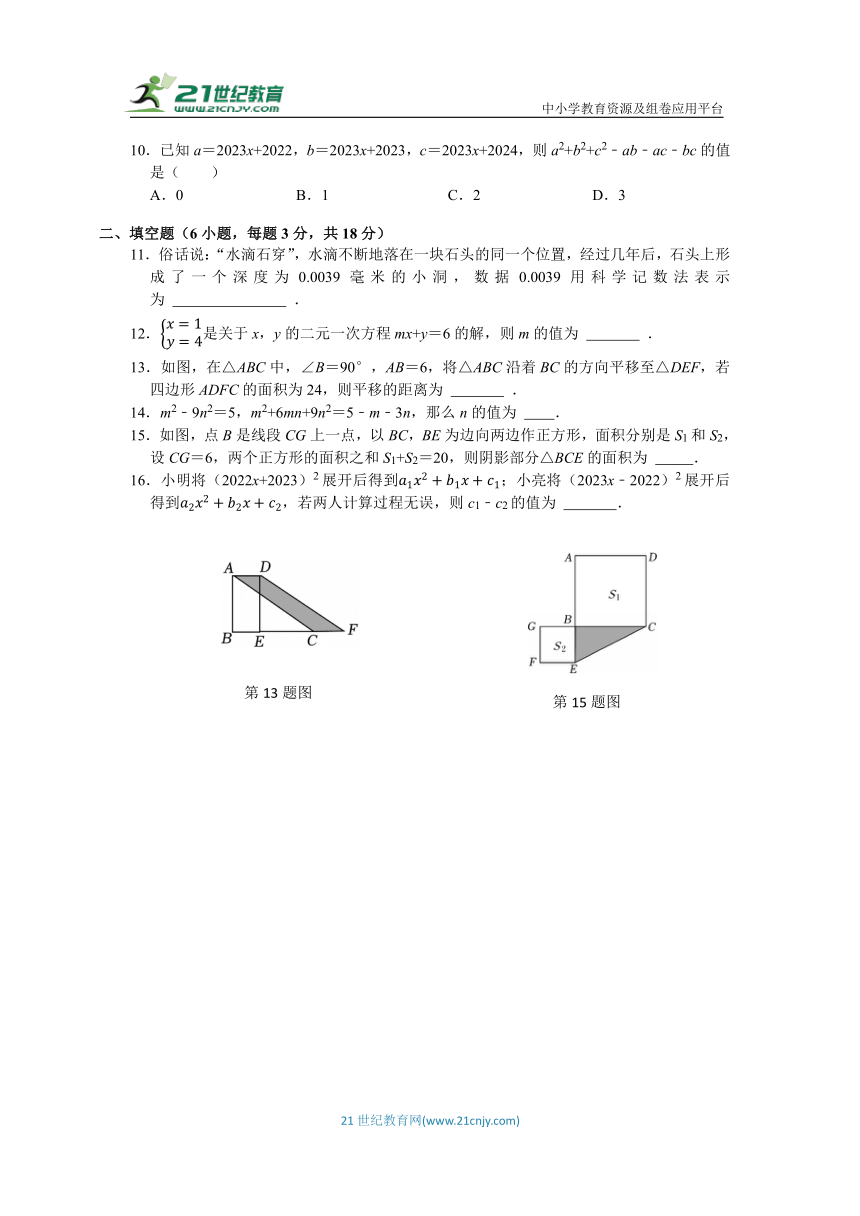
13．如图，在△ABC中，∠B＝90°，AB＝6，将△ABC沿着BC的方向平移至△DEF，若四边形ADFC的面积为24，则平移的距离为 　 　 ．
14．m2﹣9n2＝5，m2+6mn+9n2＝5﹣m﹣3n，那么n的值为 　　．
15．如图，点B是线段CG上一点，以BC，BE为边向两边作正方形，面积分别是S1和S2，设CG＝6，两个正方形的面积之和S1+S2＝20，则阴影部分△BCE的面积为 　 　．
16．小明将（2022x+2023）2展开后得到；小亮将（2023x﹣2022）2展开后得到，若两人计算过程无误，则c1﹣c2的值为 　 　．
第II卷
苏科版2024—2025学年七年级下册数学期末考试全真模拟试卷
姓名：____________ 学号：____________准考证号：___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题（17、18、19题每题6分，20、21每题8分，22、23每题9分，24、25每题10分，共计72分，解答题要有必要的文字说明）
17．（1）解不等式：﹣x+1＞2x﹣5，并把它的解集表示在数轴上；
（2）解不等式组：；
（3）解不等式组：．
18．计算：
（1）； （2）（x﹣y）（x﹣3y）﹣（2x﹣y）2．
19．求代数式（a+2）（a﹣2）﹣（a+2）2+（a+2）（a+6）的值，其中a＝﹣1．
20．如图，在△ABC中，AD是角平分线，点E、F分别在边AC、BC上，AD、BE相交于点G，且∠AGB+∠BEF＝180°．
（1）求证：∠CAD＝∠CEF；
（2）若∠BAC＝60°，∠C＝40°，求∠BFE的度数．
21．永宝电机厂计划生产一批电机设备，其中这批设备包括A型、B型两种型号，如果生产2件A型产品和3件B型产品需成本21万元，如果生产5件A型产品和4件B型产品需成本35万元．
（1）求生产一件A型产品和一件B型产品各需成本多少万元；
（2）经市场调查，一件A型产品售价为5万元，一件B型产品售价为8万元，若工厂生产这批设备中B型产品的件数是A型产品的件数2倍还多6件，销售这批设备共获利大于57万元，那么工厂生产A型产品至少多少件？
22．已知：关于x、y的二元一次方程组
（1）求5x+y的值．
（2）若方程组的解x、y满足﹣3＜x﹣y＜1，且m为整数，求m的值．
23．小明的数学研学作业单上有这样一道题：已知﹣x+y＝2，且x＜3，y≥0，设w＝x+y﹣2，那么w的取值范围是什么？
（1）小明的做法：由﹣x+y＝2得y＝2+x，则w＝x+y﹣2＝x+2+x﹣2＝2x，
由x＜3，y≥0，得关于x的一元一次不等式组 　 　 ，
解该不等式组得到x的取值范围为 　 　 ，
则w的取值范围是 　 　 .（直接填写答案，不用写过程）
（2）已知a﹣b＝n（n是大于0的常数），且a＞1，b≤1，求2a+b的最大值．（用含n的代数式表示）；
（3）若3x＝6y+12＝2z，且x＞0，y≥﹣4，z≤9，设m＝2x﹣2y﹣z，且m为整数，求m所有可能的值的和．
24．【新定义】若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”．
【举例】
方程x﹣1＝3的解为x＝4，而不等式组的解集为2＜x＜5，不难发现x＝4在2＜x＜5的范围内，所以方程x﹣1＝3是不等式组的“关联方程”．
【问题】
（1）方程3（x+1）﹣x＝9是不是不等式组的“关联方程”？请说明理由．
（2）若关于x的方程2x﹣k＝6是不等式组的“关联方程”，求k的取值范围；
（3）若关于x的方程是关于x的不等式组的“关联方程”，且此时不等式组有4个整数解，试求m的取值范围．
25．对于一个图形，通过不同的方法计算其面积可得到一些数学等式．在整式乘法的学习中，我们常借助几何图形对等式进行直观解释．如图1是一个长为4b，宽为a的长方形，沿图中虚线等分成4块小长方形．
（1）将其中2块小长方形置于一边长为a的正方形框内，摆放如图2所示．用两种不同的方法表示空白部分面积，可得到的数学等式为 　 　 ；
（2）如图3，将4块小长方形拼成一个“回形”正方形．用两种不同的方法表示空白部分面积，可得到的数学等式为 　 　 ；
（3）应用（2）中的结论解决下列问题：
①若x+y＝12，xy＝27，则x﹣y＝ 　 　 ；
②如图4，已知正方形ABCD的边长为m，E，F分别是AB，AD上的点，且BE＝4，DF＝2，长方形AEGF的面积是24，分别以GE，GF为边作正方形GEMN和正方形GHOF，求阴影部分的面积．
参考答案
一、选择题
1—10：CABCD ABBDD
二、填空题
11．【解答】解：数据0.0039用科学记数法表示为3.9×10﹣3．
故答案为：3.9×10﹣3．
12．【解答】解：∵是关于x，y的二元一次方程mx+y＝6的解，
∴m+4＝6，
解得m＝2，
故答案为：2．
13．【解答】解：由平移得：AD∥CF，AD＝CF，
∴四边形ADFC是平行四边形，
∵四边形ADFC的面积为24，∠B＝90°，
∴CF AB＝24，
∵AB＝6，
∴CF＝4，
∴平移的距离为4，
故答案为：4．
14.【解答】解：∵m2﹣9n2＝5，
∴（m+3n）（m﹣3n）＝5，
又∵m2+6mn+9n2＝5﹣m﹣3n，
∴（m+3n）（m+3n+1）＝5，
∴m﹣3n＝m+3n+1，
解得n，
故答案为：．
15．【解答】解：设BE＝a，BC＝b，
∴，，a+b＝6，
则S1+S2＝a2+b2＝20，
阴影部分的面积为BE BCab[（a+b）2﹣（a2+b2）][36﹣20]＝4，
故答案为：4．
16．【解答】解：∵（2022x+2023）2展开后得到，
∴c1＝20232，
∵（2023x﹣2022）2展开后得到，
∴c2＝20222，
∴c1﹣c2＝20232﹣20222
＝（2023+2022）（2023﹣2022）
＝4045×1
＝4045，
故答案为：4045．
三、解答题
17.【解答】解：（1）﹣x+1＞2x﹣5，
移项得：﹣2x﹣x＞﹣5﹣1，
合并同类项得：﹣3x＞﹣6．
系数化为1得：x＜2，
数轴表示为：
；
（2），
解不等式①得x＜3，
解不等式②得x，
∴原不等式组的解集为x＜3；
（3），
解不等式①得x＞2，
解不等式②得x≥4，
∴原不等式组的解集为x≥4．
18．【解答】解：（1）原式＝1+8﹣（﹣8）÷（﹣2）
＝1+8﹣4
＝5；
（2）原式＝x2﹣3xy﹣xy+3y2﹣（4x2﹣4xy+y2）
＝x2﹣3xy﹣xy+3y2﹣4x2+4xy﹣y2
＝2y2﹣3x2．
19．【解答】解：（a+2）（a﹣2）﹣（a+2）2+（a+2）（a+6）
＝a2﹣4﹣a2﹣4a﹣4+a2+8a+12
＝a2+4a+4，
当a＝﹣1时，
原式＝（﹣1）2+4×（﹣1）+4
＝1﹣4+4
＝1．
20．【解答】（1）证明：∵∠AGB+∠BEF＝180°，∠AGB+∠AGE＝180°，
∴∠AGE＝∠BEF，
∴EF∥AD，
∴∠CAD＝∠CEF；
（2）解：∵∠BAC＝60°，∠C＝40°，
∴∠ABC＝180°﹣60°﹣40°＝80°，
∵AD是角平分线，
∴∠BAD∠BAC＝30°，
∴∠ADB＝180°﹣80°﹣30°＝70°，
∵EF∥AD，
∴∠BFE＝∠ADB＝70°．
21.【解答】解：（1）设生产一件A型产品需成本x万元，一件B型产品需成本y万元，
根据题意得：，
解得：．
答：生产一件A型产品需成本3万元，一件B型产品需成本5万元；
（2）设工厂生产A型产品m件，则生产B型产品（2m+6）件，
根据题意得：（5﹣3）m+（8﹣5）（2m+6）＞57，
解得：m，
又∵m为正整数，
∴m的最小值为5．
答：工厂生产A型产品至少5件．
22.【解答】解：（1）①+②得：4x＝6﹣2m，
解得x，
把x代入①得：y，
∴5x+y＝57；
（2）∵方程组的解x、y满足﹣3＜x﹣y＜1，
∴﹣31，
解得m，
又∵m为整数，
∴m的值为1．
23.【解答】解：（1）小明的做法：由﹣x+y＝2得y＝2+x，则w＝x+y﹣2＝x+2+x﹣2＝2x，
由x＜3，y≥0，得关于x的一元一次不等式组，
解该不等式组得到x的取值范围为﹣2≤x＜3，则w的取值范围是﹣4≤w＜6；
故答案为：，﹣2≤x＜3，﹣4≤w＜6；
（2）∵a﹣b＝n，
∴b＝a﹣n，
∵a＞1，b≤1，
∴关于a的一元一次不等式组，
解得1＜a≤n+1，
设t＝2a+b＝2a+a﹣n＝3a﹣n，
∴3﹣n＜t≤2n+3，
∴2a+b的最大值为2n+3；
（3）∵3x＝6y+12，
∴x＝2y+4，
∵6y+12＝2z，
∴z＝3y+6，
∴关于y的一元一次不等式为，
解得﹣2＜y≤1，
∵m＝2x﹣2y﹣z＝2（2y+4）﹣2y﹣（3y+6）＝﹣y+2，
∴1≤m＜4，
∵m为正数，
∴m＝1，2，3，
∴m所有可能的值的和为6．
24.【解答】解：（1）方程3（x+1）﹣x＝9是不等式组的“关联方程”．理由如下：
由方程3（x+1）﹣x＝9，
解得：x＝3．
解不等式组，
可得原不等式组的解集为：1＜x≤5，
∵x＝3在1＜x≤5的范围内，
∴方程3（x+1）﹣x＝9是不等式组的“关联方程”．
（2），
解不等式①得：x≥﹣1，
解不等式②得：x≤7，
∴原不等式组的解集为：﹣1≤x≤7，
由方程2x﹣k＝6，
解得：．
∵关于x的方程2x﹣k＝6是不等式组的“关联方程”，
∴，
解得：﹣8≤k≤8．
（3）由关于x的方程，
解得：x＝6m﹣7，
，
解不等式①得：x＞0，
解不等式②得：x≤3m+1，
∴原不等式组的解集为：0＜x≤3m+1，
∵不等式组有4个整数解，
∴整数的值为1，2，3，4，
∴4≤3m+1＜5，
∴．
∵关于x的方程是关于x的不等式组的“关联方程”，
∴，
解得：，
∴m的取值范围：．
25.【解答】解：（1）图2中，空白部分是边长为a﹣b的正方形，因此面积为（a﹣b）2，整体大正方形的边长为a，因此面积为a2，阴影部分的面积为2ab﹣b2，
所以有（a﹣b）2＝a2﹣（2ab﹣b2）＝a2﹣2ab+b2，
故答案为：（a﹣b）2＝a2﹣2ab+b2；
（2）图3中，空白部分是边长为a﹣b的正方形，因此面积为（a﹣b）2，整体大正方形的边长为a+b，因此面积为（a+b）2，阴影部分的面积为4ab，
所以有（a﹣b）2＝（a+b）2﹣4ab，
故答案为：（a﹣b）2＝（a+b）2﹣4ab；
（3）①∵x+y＝12，xy＝27，
∴（x﹣y）2＝（x+y）2﹣4xy
＝144﹣4×27
＝36，
x﹣y＝±6，
故答案为：±6；
②∵正方形ABCD的边长为m，BE＝4，DF＝2，
∴长方形AEGF的长AF＝m﹣2，宽AE＝m﹣4，
∵长方形AEGF面积是24，
∴（m﹣2）（m﹣4）＝24，
设a＝m﹣2，b＝m﹣4，则a﹣b＝2，ab＝24，
∵（a﹣b）2＝（a+b）2﹣4ab，即4＝（a+b）2﹣4×24；
∴（a+b）2＝100，
∴a+b＝10（取正值），
∴S阴影部分＝S正方形EGNM﹣S正方形OFGH
＝（m﹣2）2﹣（m﹣4）2
＝a2﹣b2
＝（a+b）（a﹣b）
＝10×2
＝20．
答：阴影部分的面积为20．
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑