资源简介

2020-2021学年北师大版九年级上册数学期末复习试卷
一．选择题（共11小题，满分33分，每小题3分）
1．若|x+2|+（y﹣3）2＝0，则x﹣y的值为（　　）
A．﹣5
B．5
C．1
D．﹣1
2．世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为0.056盎司．将0.056用科学记数法表示为（　　）
A．5.6×10﹣1
B．5.6×10﹣2
C．5.6×10﹣3
D．0.56×10﹣1
3．下列图形经过折叠不能围成棱柱的是（　　）
A．
B．
C．
D．
4．△ABC的三个顶点的横坐标都乘以﹣1，纵坐标不变，则所得三角形与原三角形的位置关系是（　　）
A．关于x轴对称
B．关于y轴对称
C．关于原点对称
D．将△ABC向右平移了1个单位长度
5．已知x+y+2（﹣x﹣y+1）＝3（1﹣y﹣x）﹣4（y+x﹣1），则x+y等于（　　）
A．﹣
B．
C．﹣
D．
6．已知直线m∥n，将一块含30°角的直角三角板ABC，按如图所示方式放置，其中A、B两点分别落在直线m、n，若∠1＝35°20'，则∠2的度数是（　　）
A．35°20'
B．35°40'
C．24°40'
D．24°80'
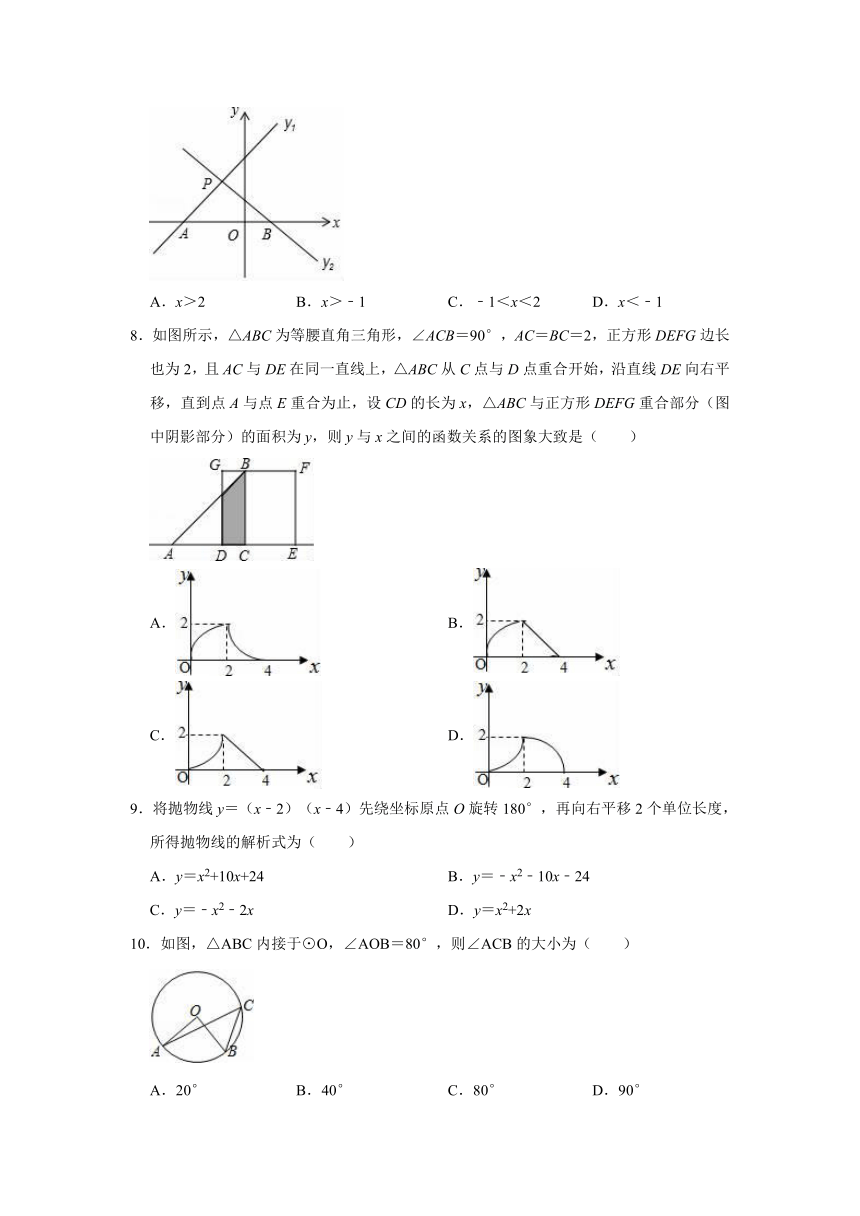
7．如图，已知直线y1＝k1x+m和直线y2＝k2x+n交于点P（﹣1，2），则关于x的不等式（k1﹣k2）x＞﹣m+n的解集是（　　）
A．x＞2
B．x＞﹣1
C．﹣1＜x＜2
D．x＜﹣1
8．如图所示，△ABC为等腰直角三角形，∠ACB＝90°，AC＝BC＝2，正方形DEFG边长也为2，且AC与DE在同一直线上，△ABC从C点与D点重合开始，沿直线DE向右平移，直到点A与点E重合为止，设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（　　）
A．
B．
C．
D．
9．将抛物线y＝（x﹣2）（x﹣4）先绕坐标原点O旋转180°，再向右平移2个单位长度，所得抛物线的解析式为（　　）
A．y＝x2+10x+24
B．y＝﹣x2﹣10x﹣24
C．y＝﹣x2﹣2x
D．y＝x2+2x
10．如图，△ABC内接于⊙O，∠AOB＝80°，则∠ACB的大小为（　　）
A．20°
B．40°
C．80°
D．90°
11．如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN＝20，AC＝8，BD＝6，则PA+PB的最小值是（　　）
A．20
B．
C．14
D．
二．填空题（共4小题，满分12分，每小题3分）
12．分解因式：x2﹣9x＝　
　．
13．如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是　
　．
14．已知点A（1，5），B（5，n）均在反比例函数y＝的图象上，点C与点D分别在x轴和直线y＝2x﹣4的图象上，若以A，B，C，D为顶点的四边形是平行四边形，则点D的坐标为　
　．
15．在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律下去，第6个正方形的面积为　
　．
三．解答题（共7小题）
16．计算：
17．先化简，再求值：（x﹣2+）÷，其中x＝﹣．
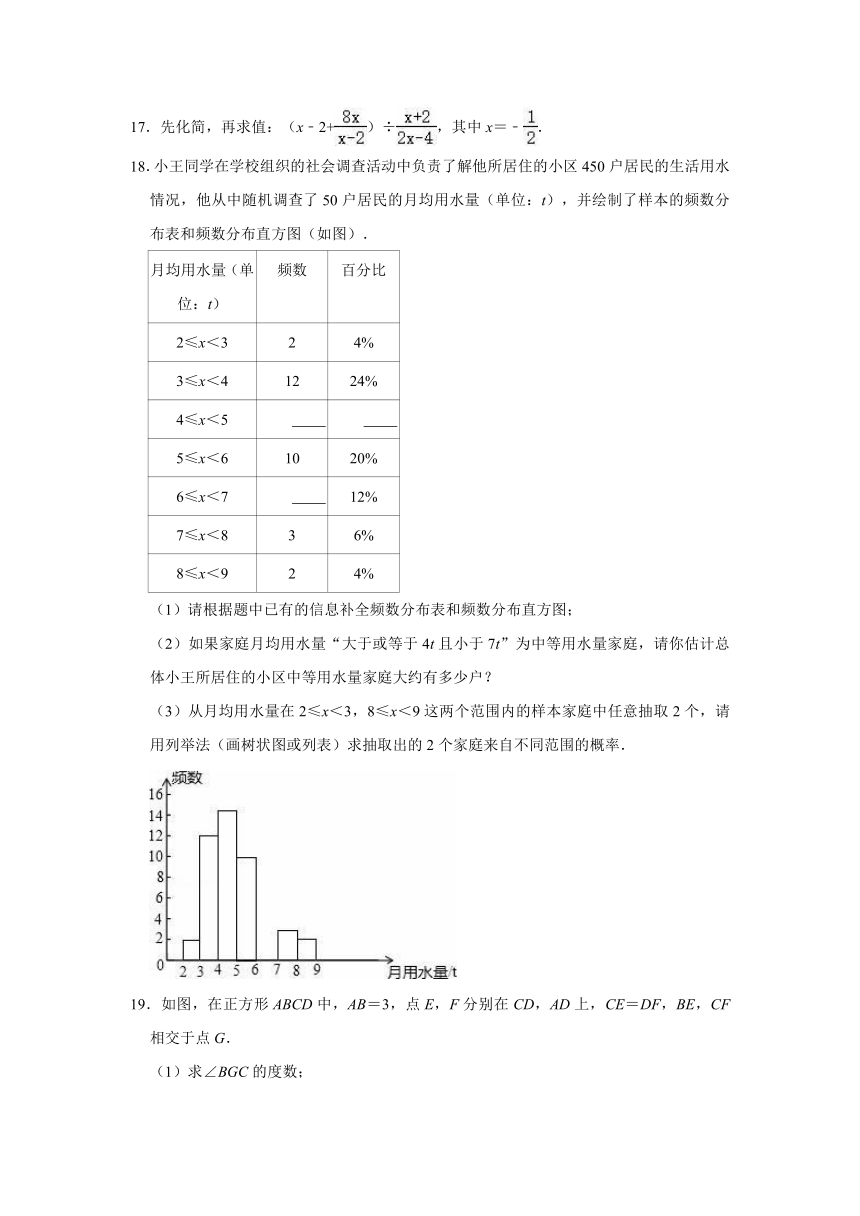
18．小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．
月均用水量（单位：t）
频数
百分比
2≤x＜3
2
4%
3≤x＜4
12
24%
4≤x＜5
　
　
　
　
5≤x＜6
10
20%
6≤x＜7
　
　
12%
7≤x＜8
3
6%
8≤x＜9
2
4%
（1）请根据题中已有的信息补全频数分布表和频数分布直方图；
（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你估计总体小王所居住的小区中等用水量家庭大约有多少户？
（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列举法（画树状图或列表）求抽取出的2个家庭来自不同范围的概率．
19．如图，在正方形ABCD中，AB＝3，点E，F分别在CD，AD上，CE＝DF，BE，CF相交于点G．
（1）求∠BGC的度数；
（2）若CE＝1，H为BF的中点时，求HG的长度；
（3）若图中阴影部分的面积与正方形ABCD的面积之比为2：3，求△BCG的周长．
20．2020年1月份，为抗击新型冠状病毒，某药店计划购进一批甲、乙两种型号的口罩，已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元，用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同．
（1）求每袋甲种、乙种口罩的进价分别是多少元？
（2）该药店计划购进甲、乙两种口罩共480袋，其中甲种口罩的袋数少于乙种口罩袋数的，药店决定此次进货的总资金不超过10000元，求商场共有几种进货方案？
21．已知，正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．
（1）如图①，当∠MAN绕点A旋转到BM＝DN时，请你直接写出AH与AB的数量关系：　
　；
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
（3）如图③，已知∠MAN＝45°，AH⊥MN于点H，且MH＝2，NH＝3，求AH的长．（可利用（2）得到的结论）
22．如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y＝﹣x2+bx+c经过点A、C，与AB交于点D．
（1）求抛物线的函数解析式；
（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．
①求S关于m的函数表达式；
②当S最大时，在抛物线y＝﹣x2+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．
参考答案与试题解析
一．选择题（共11小题，满分33分，每小题3分）
1．解：∵|x+2|+（y﹣3）2＝0，
∴x+2＝0，y﹣3＝0，
解得：x＝﹣2，y＝3，
故x﹣y＝﹣2﹣3＝﹣5．
故选：A．
2．解：将0.056用科学记数法表示为5.6×10﹣2，
故选：B．
3．解：A可以围成四棱柱，C可以围成五棱柱，D可以围成三棱柱，B选项侧面上多出一个长方形，故不能围成一个三棱柱．
故选：B．
4．解：∵横坐标都乘以﹣1，纵坐标不变，
∴对应点的横坐标互为相反数，纵坐标不变，
∴对应点关于y轴对称，
∴所得图形关于y轴对称，
故选：B．
5．解：方法1：
∵x+y+2（﹣x﹣y+1）＝3（1﹣y﹣x）﹣4（y+x﹣1）
∴x+y﹣2x﹣2y+2＝3﹣3y﹣3x﹣4y﹣4x+4
∴﹣x﹣y+2＝7﹣7y﹣7x
∴6x+6y＝5
∴x+y＝
方法2：
∵x+y+2（﹣x﹣y+1）＝3（1﹣y﹣x）﹣4（y+x﹣1）
∴（x+y）﹣2（x+y）+2＝3﹣3（x+y）﹣4（x+y）+4
∴（x+y）﹣2（x+y）+3（x+y）+4（x+y）＝3+4﹣2
∴6（x+y）＝5
∴x+y＝
故选：D．
6．解：∵直线m∥n，
∴∠3＝∠1＝35°20′，
又∵△ABC中，∠ABC＝60°，
∴∠2＝60°﹣35°20′＝24°40'，
故选：C．
7．解：由图形可知，当x＞﹣1时，k1x+m＞k2x+n，即（k1﹣k2）x＞﹣m+n，
所以，关于x的不等式（k1﹣k2）x＞﹣m+n的解集是x＞﹣1．
故选：B．
8．解：设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，
当C从D点运动到E点时，即0≤x≤2时，y＝×2×2﹣（2﹣x）×（2﹣x）＝﹣x2+2x．
当A从D点运动到E点时，即2＜x≤4时，y＝×[2﹣（x﹣2）]×[2﹣（x﹣2）]＝x2﹣4x+8，
∴y与x之间的函数关系由函数关系式可看出A中的函数图象与所求的分段函数对应．
故选：A．
9．解：y＝（x﹣2）（x﹣4）＝（x﹣3）2﹣1．此时，该抛物线顶点坐标是（3，﹣1）．
将该抛物线绕坐标原点O旋转180°后的顶点坐标是（﹣3，1）．再向右平移2个单位长度后的顶点坐标是（﹣1，1）．
所以此时抛物线的解析式为：y＝﹣（x+1）2+1＝﹣x2﹣2x．
故选：C．
10．解：∵△ABC内接于⊙O，∠AOB＝80°，
∴∠ACB＝∠AOB＝40°．
故选：B．
11．解：∵MN＝20，
∴⊙O的半径＝10，
连接OA、OB，
在Rt△OBD中，OB＝10，BD＝6，
∴OD＝＝＝8；
同理，在Rt△AOC中，OA＝10，AC＝8，
∴OC＝＝＝6，
∴CD＝8+6＝14，
作点B关于MN的对称点B′，连接AB′，则AB′即为PA+PB的最小值，B′D＝BD＝6，过点B′作AC的垂线，交AC的延长线于点E，
在Rt△AB′E中，
∵AE＝AC+CE＝8+6＝14，B′E＝CD＝14，
∴AB′＝＝＝14．
故选：B．
二．填空题（共4小题，满分12分，每小题3分）
12．解：原式＝x?x﹣9?x＝x（x﹣9），
故答案为：x（x﹣9）．
13．解：黑色区域的面积＝3×3﹣×3×1﹣×2×2﹣×3×1＝4，
所以击中黑色区域的概率＝．
故答案为：．
14．解：∵点A（1，5），B（5，n）均在反比例函数y＝的图象上，
∴k＝1×5＝5n，
∴n＝1，
∴B（5，n），
∵以A，B，C，D为顶点的四边形是平行四边形，
∴D到x轴的距离为5﹣1＝4，
当y＝4时，代入y＝2x﹣4得，4＝2x﹣4，
解得x＝4，
∴D（4，4），
当y＝﹣4时，代入y＝2x﹣4得，﹣4＝2x﹣4，
解得x＝0，
∴D（0，﹣4），
综上，点D的坐标为（4，4）或（0，﹣4）．
故答案为（4，4）或（0，﹣4）．
15．解：∵点A（1，0），点D（0，2），
∴OA＝1，OD＝2，
∴由勾股定理得：AD＝＝＝，
∵∠ADO+∠DAO＝90°，∠DAO+∠BAA1＝90°，
∴∠ADO＝∠BAA1，
又∵∠AOD＝∠ABA1＝90°，
∴△AOD∽△A1BA，
∴＝，
∴A1B＝＝，
∴第2个正方形的边长A1C＝A1B1＝+＝；
同理A2B1＝×＝；
∴第3个正方形的边长A2C1＝A2B2＝+＝＝；
第4个正方形的边长为：
+＝，
…，
∴第6个正方形的边长为：
，
∴第6个正方形的面积为：
×＝5×．
故答案为：5×．
三．解答题（共7小题）
16．解：原式＝2×﹣3+1﹣9
＝1﹣3+1﹣9
＝﹣10．
17．解：原式＝（+）?
＝?
＝2（x+2）
＝2x+4，
当x＝﹣时，
原式＝2×（﹣）+4
＝﹣1+4
＝3．
18．解：（1）调查的总数是：2÷4%＝50（户），
则6≤x＜7部分调查的户数是：50×12%＝6（户），
则4≤x＜5的户数是：50﹣2﹣12﹣10﹣6﹣3﹣2＝15（户），
所占的百分比是：×100%＝30%．
故答案为：15，30%，6；
补全频数分布表和频数分布直方图，如图所示：
（2）中等用水量家庭大约有450×（30%+20%+12%）＝279（户）；
答：估计总体小王所居住的小区中等用水量家庭大约有279户；
（3）在2≤x＜3范围的两户用a、b表示，
8≤x＜9这两个范围内的两户用1，2表示．
画树状图：
共有12种等可能情况，满足抽取出的2个家庭来自不同范围的共有8种，
则抽取出的2个家庭来自不同范围的概率是：＝．
19．解：（1）∵四边形ABCD是正方形，
∴BC＝CD，∠BCD＝∠CDF＝90°，
在△BCE和△CDF中，∵BC＝CD，∠BCD＝∠CDF，CE＝DF，
∴△BCE≌△CDF（SAS），
∴∠CBE＝∠DCF，
又∵∠BCG+∠DCF＝90°，
∴∠BCG+∠CBE＝90°，
∴∠BGC＝90°；
（2）如图，∵CE＝1，
∴DF＝1，
∴AF＝2，
在直角△ABF中，由勾股定理得：，
∵H为BF的中点，∠BGF＝90°，
∴；
（3）∵阴影部分的面积与正方形ABCD的面积之比为2：3，
∴阴影部分的面积为×9＝6，
∴空白部分的面积为9﹣6＝3，
∵△BCE≌△CDF，
∴△BCG的面积与四边形DEGF的面积相等，均为×3＝，
设BG＝a，CG＝b，则ab＝，
∴ab＝3，
又∵a2+b2＝32，
∴a2+2ab+b2＝9+6＝15，
即（a+b）2＝15，
∴a+b＝，即BG+CG＝，
∴△BCG的周长＝+3．
20．解：（1）设甲种口罩进价x元/袋，则乙种口罩进价为（40﹣x）元/袋，依题意有
＝，
解得x＝15，
经检验x＝15是原方程的解，
则40﹣x＝25．
故甲种口罩进价15元/袋，则乙种口罩进价为25元/袋；
（2）设购进甲种口罩y袋，则购进乙种口罩（480﹣y）袋，依题意有
，
解得200≤y＜204．
因为y是整数，甲种口罩的袋数少于乙种口罩袋数，
所以y取200，201，202，203，共有4种方案．
21．解：（1）如图①AH＝AB．
（2）数量关系成立．如图②，延长CB至E，使BE＝DN．
∵ABCD是正方形，
∴AB＝AD，∠D＝∠ABE＝90°，
在Rt△AEB和Rt△AND中，，
∴Rt△AEB≌Rt△AND，
∴AE＝AN，∠EAB＝∠NAD，
∵∠DAN+∠BAM＝45°，
∴∠EAB+∠BAM＝45°，
∴∠EAM＝45°，
∴∠EAM＝∠NAM＝45°，
在△AEM和△ANM中，，
∴△AEM≌△ANM．
∴S△AEM＝S△ANM，EM＝MN，
∵AB、AH是△AEM和△ANM对应边上的高，
∴AB＝AH．
（3）如图③分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，
∴BM＝2，DN＝3，∠B＝∠D＝∠BAD＝90°．
分别延长BM和DN交于点C，得正方形ABCD，
由（2）可知，AH＝AB＝BC＝CD＝AD．
设AH＝x，则MC＝x﹣2，NC＝x﹣3，
在Rt△MCN中，由勾股定理，得MN2＝MC2+NC2
∴52＝（x﹣2）2+（x﹣3）2
解得x1＝6，x2＝﹣1．（不符合题意，舍去）
∴AH＝6．
22．解：（1）将A、C两点坐标代入抛物线，得
，
解得：，
∴抛物线的解析式为y＝﹣x2+x+8；
（2）①∵OA＝8，OC＝6，
∴AC＝＝10，
过点Q作QE⊥BC与E点，则sin∠ACB＝＝＝，
∴＝，
∴QE＝（10﹣m），
∴S＝?CP?QE＝m×（10﹣m）＝﹣m2+3m；
②∵S＝?CP?QE＝m×（10﹣m）＝﹣m2+3m＝﹣（m﹣5）2+，
∴当m＝5时，S取最大值；
在抛物线对称轴l上存在点F，使△FDQ为直角三角形，
∵抛物线的解析式为y＝﹣x2+x+8的对称轴为x＝，
D的坐标为（3，8），Q（3，4），
当∠FDQ＝90°时，F1（，8），
当∠FQD＝90°时，则F2（，4），
当∠DFQ＝90°时，设F（，n），
则FD2+FQ2＝DQ2，
即+（8﹣n）2++（n﹣4）2＝16，
解得：n＝6±，
∴F3（，6+），F4（，6﹣），
满足条件的点F共有四个，坐标分别为
F1（，8），F2（，4），F3（，6+），F4（，6﹣）．

展开更多......

收起↑