资源简介

第九讲 作辅助线构造全等三角
知识要点：
学习各种方法，作适当的辅助线构造全等三角形
新知讲授
一、题目中涉及角平分线 ,通常以角平分线为公共边来构造全等三角形.
1. 如图,在ΔABC中,∠C=900,AD平分∠BAC,BC=40,线段DC与DB的长度的比为3∶5,求D点到AB的距离.
2.如图,ΔABC中,∠C=900,CA=CB,AD平分∠BAC.试问:能否在AB上确定一点E,使ΔBDE的周长等于AB 请说明理由.
3.如图,ΔABC中,AB=2AC,∠1=∠2,DA=DB.求证:∠ACD=900.(要求用两种方法)
证法一:延长AC到F,使AF=AB,连结DF.
证法二:作DE⊥AB于E.
4.如图,ΔABC中,∠1=∠2, 且AB=AC+CD.求证:∠C=2∠B. (要求用两种方法)
证法一:延长AC到F,使CF=CD,连结DF. 　　　　　　　　　　　　
证法二:在AB上截取AE=AC,连结DE.
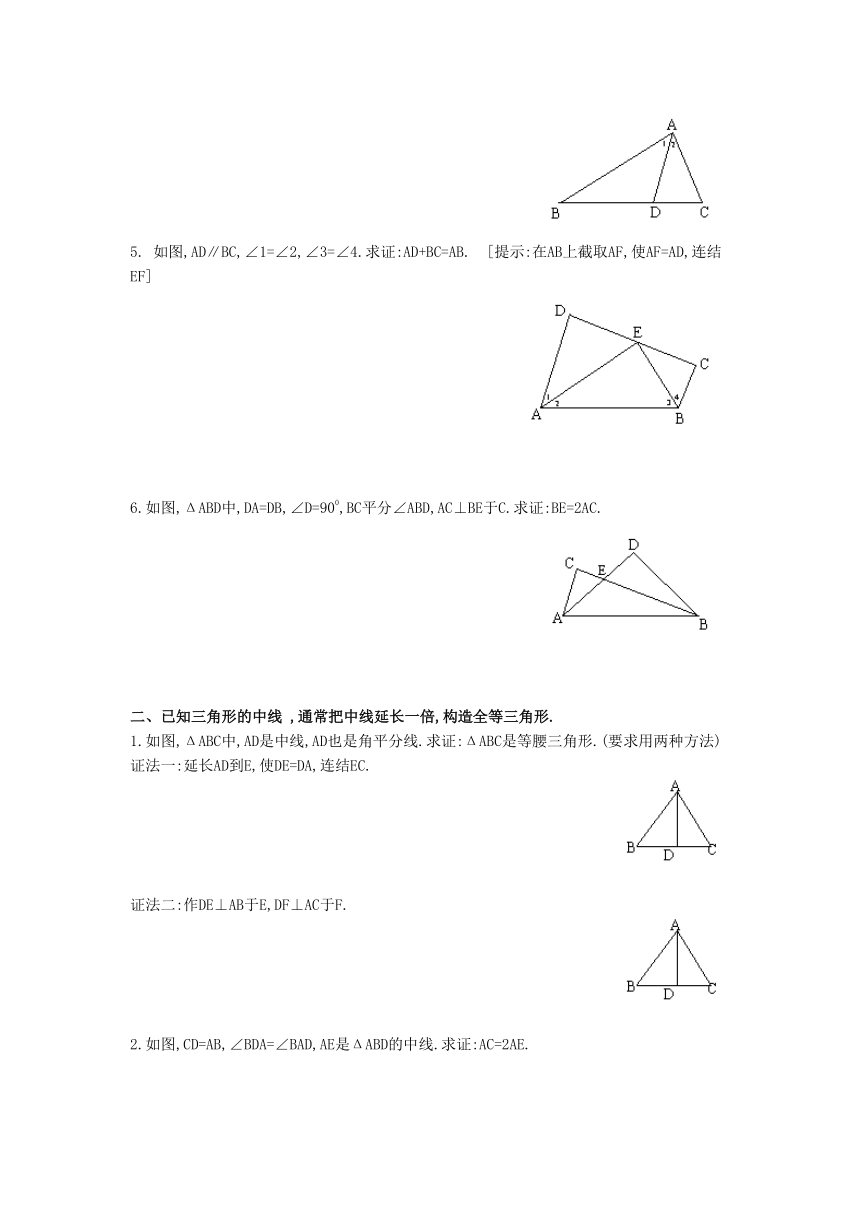
5. 如图,AD∥BC,∠1=∠2,∠3=∠4.求证:AD+BC=AB. [提示:在AB上截取AF,使AF=AD,连结EF]
6.如图,ΔABD中,DA=DB,∠D=900,BC平分∠ABD,AC⊥BE于C.求证:BE=2AC.
二、已知三角形的中线 ,通常把中线延长一倍,构造全等三角形.
1.如图,ΔABC中,AD是中线,AD也是角平分线.求证:ΔABC是等腰三角形.(要求用两种方法)
证法一:延长AD到E,使DE=DA,连结EC.
证法二:作DE⊥AB于E,DF⊥AC于F.
2.如图,CD=AB,∠BDA=∠BAD,AE是ΔABD的中线.求证:AC=2AE.
3. 已知:如图,AD是ΔABC的中线.求证:AB+AC>2AD.
4.证明定理 直角三角形的斜边上的中线等于斜边的一半.
已知:在ΔABC中,∠ACB=900,CD是斜边AB上的中线.
求证:CD=AB. [提示:延长AD到E,使DE=DA,连结EB.先证EB=AC,∠EBC=900,再证ΔACBΔEBC]
5.已知:如图,ΔABC中,AD平分∠BAC,M是BC的中点,ME∥AD.求证:BF=CE.
6.如图,已知:ΔABC中,D是BC的中点,DE⊥DF.求证:BE+CF>EF.
[提示:延长ED到G,使DG=DE,连结GC和GF,先证EF=GF,BE=CG]

展开更多......

收起↑