资源简介

专项训练五　常考相似模型
类型一　A字型
有一个公共角(∠A),此时需要找另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论.
1.图3和图5:AC2=AD·AB.
2.图5:(1)CD2=AD·BD.
(2)BC2=BD·AB.
① (2024·湖南)如图,在△ABC中,点D,E分别为边AB,AC的中点.下列结论中,错误的是 (　　)
A.DE∥BC B.△ADE∽△ABC
C.BC=2DE D.S△ADE=S△ABC
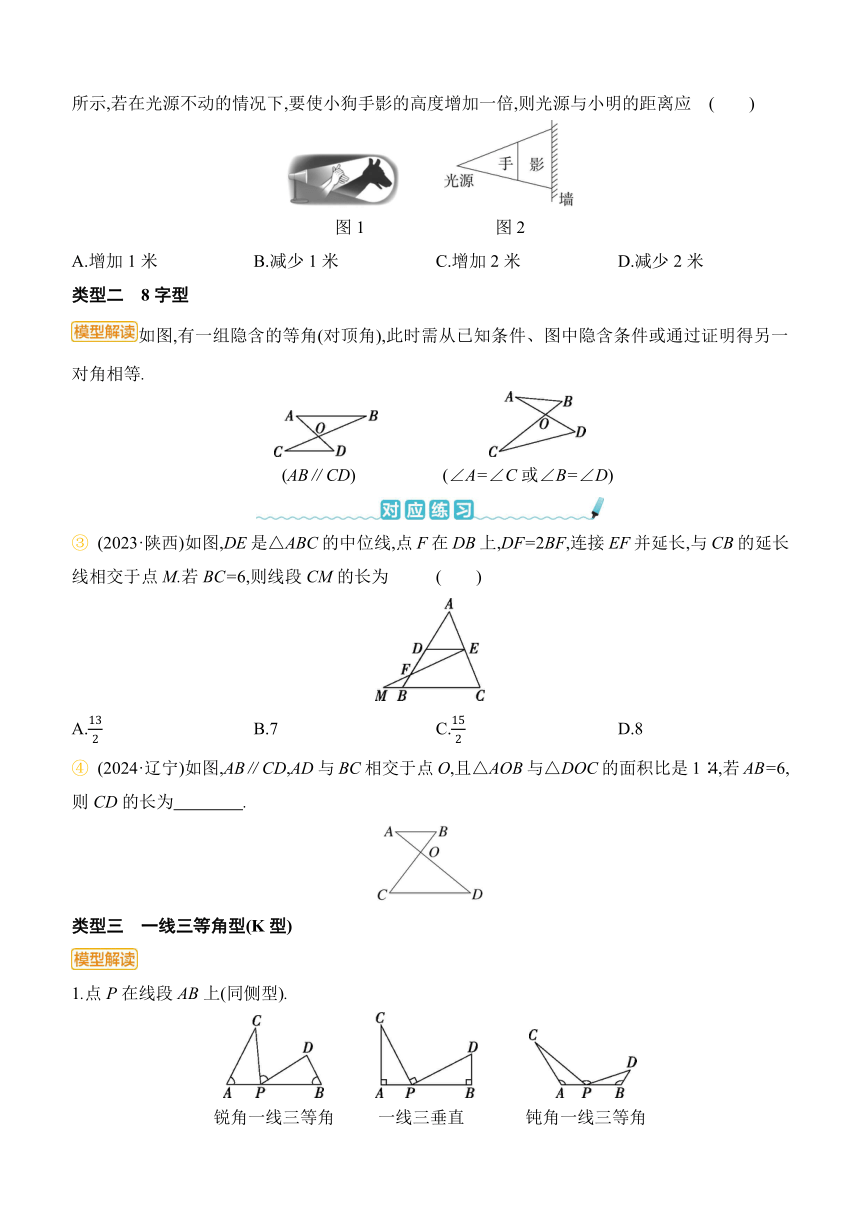
② (2024·河北模拟)手影游戏利用的物理原理是光是沿直线传播的.图1中小狗手影就是我们小时候常玩的游戏.在一次游戏中,小明距离墙壁2米,爸爸拿着的光源与小明的距离为4米,如图2所示,若在光源不动的情况下,要使小狗手影的高度增加一倍,则光源与小明的距离应 (　　)
图1　 图2
A.增加1米 B.减少1米 C.增加2米 D.减少2米
类型二　8字型
如图,有一组隐含的等角(对顶角),此时需从已知条件、图中隐含条件或通过证明得另一对角相等.
(AB∥CD)　 　(∠A=∠C或∠B=∠D)
③ (2023·陕西)如图,DE是△ABC的中位线,点F在DB上,DF=2BF,连接EF并延长,与CB的延长线相交于点M.若BC=6,则线段CM的长为 (　　)
A. B.7 C. D.8
④ (2024·辽宁)如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1∶4,若AB=6,则CD的长为　　　　.
类型三　一线三等角型(K型)
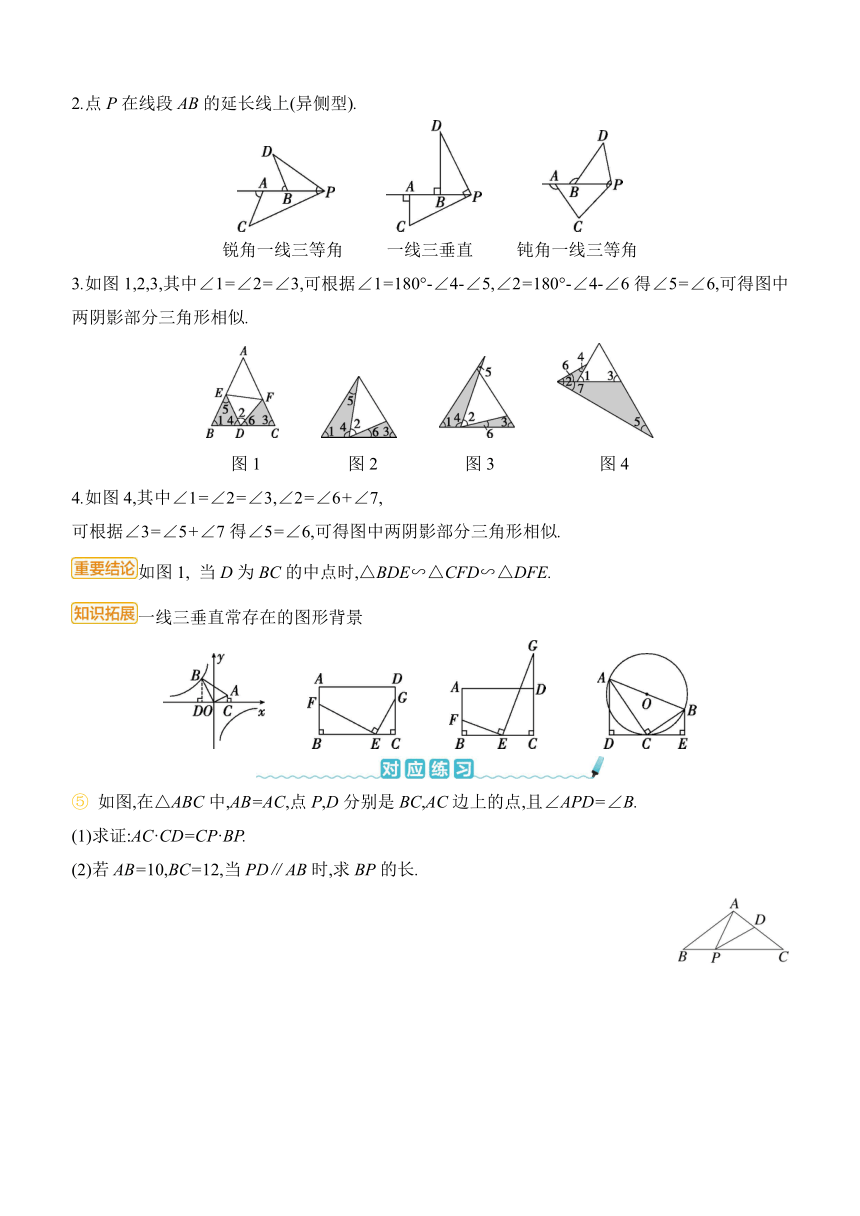
1.点P在线段AB上(同侧型).
锐角一线三等角 一线三垂直 钝角一线三等角
2.点P在线段AB的延长线上(异侧型).
锐角一线三等角　 一线三垂直　 钝角一线三等角
3.如图1,2,3,其中∠1=∠2=∠3,可根据∠1=180°-∠4-∠5,∠2=180°-∠4-∠6得∠5=∠6,可得图中两阴影部分三角形相似.
图1 图2 图3 图4
4.如图4,其中∠1=∠2=∠3,∠2=∠6+∠7,
可根据∠3=∠5+∠7得∠5=∠6,可得图中两阴影部分三角形相似.
如图1, 当D为BC的中点时,△BDE∽△CFD∽△DFE.
一线三垂直常存在的图形背景
⑤ 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP.
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
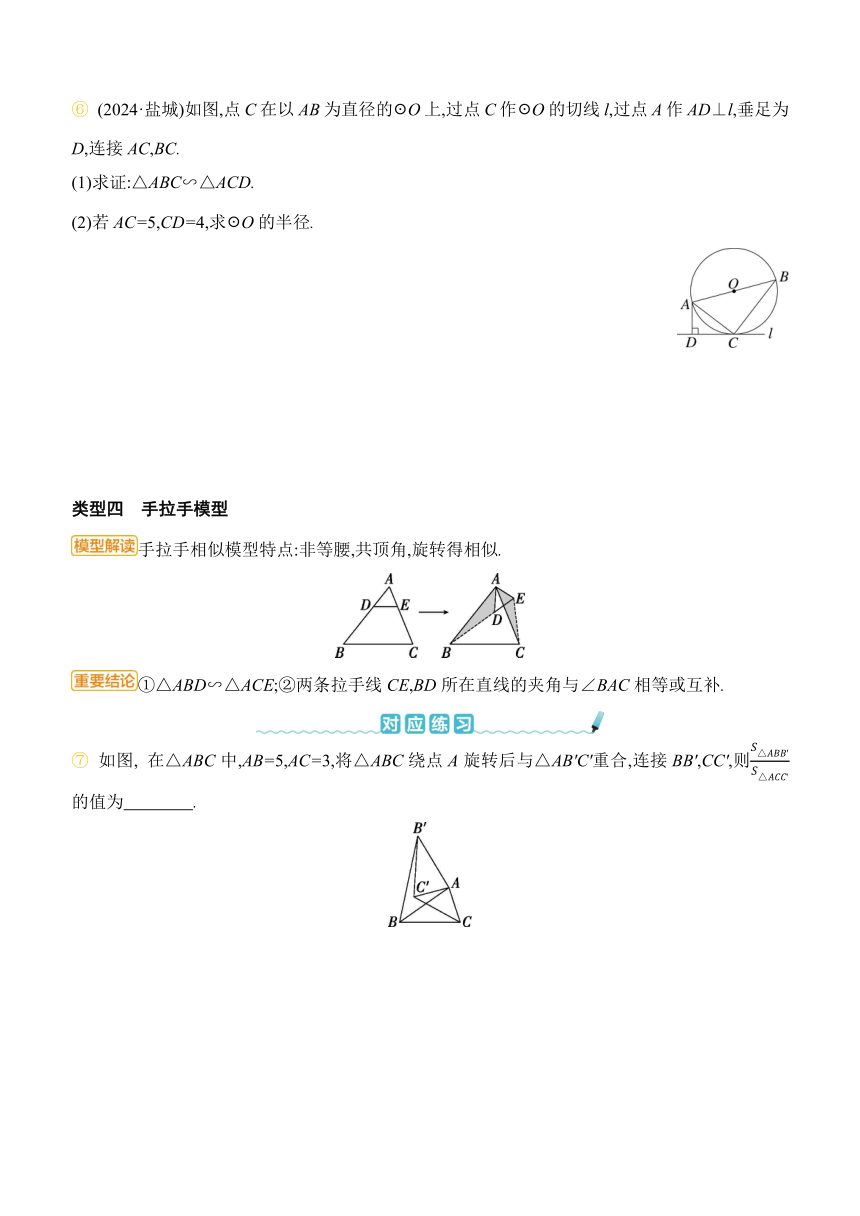
⑥ (2024·盐城)如图,点C在以AB为直径的☉O上,过点C作☉O的切线l,过点A作AD⊥l,垂足为D,连接AC,BC.
(1)求证:△ABC∽△ACD.
(2)若AC=5,CD=4,求☉O的半径.
类型四　手拉手模型
手拉手相似模型特点:非等腰,共顶角,旋转得相似.
①△ABD∽△ACE;②两条拉手线CE,BD所在直线的夹角与∠BAC相等或互补.
⑦ 如图, 在△ABC中,AB=5,AC=3,将△ABC绕点A旋转后与△AB'C'重合,连接BB',CC',则的值为　　　　.
【详解答案】
对应练习
1.D　解析:∵点D,E分别为边AB,AC的中点,
∴DE是△ABC的中位线,∴DE∥BC,BC=2DE.
故A,C选项不符合题意.
∵DE∥BC,
∴△ADE∽△ABC.
故B选项不符合题意.
∵△ADE∽△ABC,
∴=2=,
则S△ADE=S△ABC.
故D选项符合题意.故选D.
2.D　解析:如图1,点O为光源,AB表示小明的手,CD表示小狗手影,则AB∥CD,过点O作OE⊥AB,延长OE交CD于点F,则OF⊥CD,
图1
∵AB∥CD,∴∠OAB=∠OCD,∠OBA=∠ODC,
∴△AOB∽△COD,∴.
∵EF=2米,OE=4米,则OF=6米,
∴,
设AB=2k,则CD=3k,
∵在光源不动的情况下,要使小狗手影的高度增加一倍,如图2,
图2
即AB=2k,
C'D'=6k,
∵△AO'B∽△C'O'D',
∴,
则O'E'=2米,
∴光源与小明的距离减少OE-O'E'=4-2=2(米),
故选D.
3.C　解析:∵DE是△ABC的中位线,∴DE∥BC,DE=BC.
∵BC=6,∴DE=BC=3.
∵DE∥BC,
∴△DEF∽△BMF.
∴,∵DF=2BF,∴=2,∴BM=,
∴CM=+6=.故选C.
4.12　解析:∵AB∥CD,
∴△AOB∽△DOC,
∴=2=,
∴.
∵AB=6,
∴,
∴DC=12.
5.解:(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠B=∠C.
∵∠APC=∠BAP+∠B,
∠APC=∠APD+∠CPD,
∴∠BAP=∠CPD,
∴△ABP∽△PCD,∴,
∴AB·CD=PC·BP.
∵AB=AC,∴AC·CD=CP·BP.
(2)∵PD∥AB,
∴∠APD=∠BAP.
∵∠APD=∠C,∴∠BAP=∠C.
又∵∠B=∠B,
∴△BAP∽△BCA,∴.
∵AB=10,BC=12,∴,
∴BP=.
6.解:(1)证明:如图,连接OC,
∵l是☉O的切线,
∴OC⊥l.
∵AD⊥l,
∴OC∥AD,
∴∠CAD=∠ACO=∠CAB.
∵∠ADC=∠ACB=90°,
∴△ABC∽△ACD.
(2)∵AC=5,CD=4,∠ADC=90°,
∴AD==3.
∵△ABC∽△ACD,
∴,
∴,
∴AB=,
∴☉O的半径为.
7.　解析:由旋转得△ABC≌△AB'C',
∴AB= AB',AC=AC',∠BAC=
∠B'AC'.
∴∠BAB'=∠CAC',且,
∴△ABB'∽△ACC'.
∴=2=2=.

展开更多......

收起↑