资源简介

中小学教育资源及组卷应用平台
期末综合测试卷
时间：90分钟 满分：120分
一、选择题(每题3分，共30分)
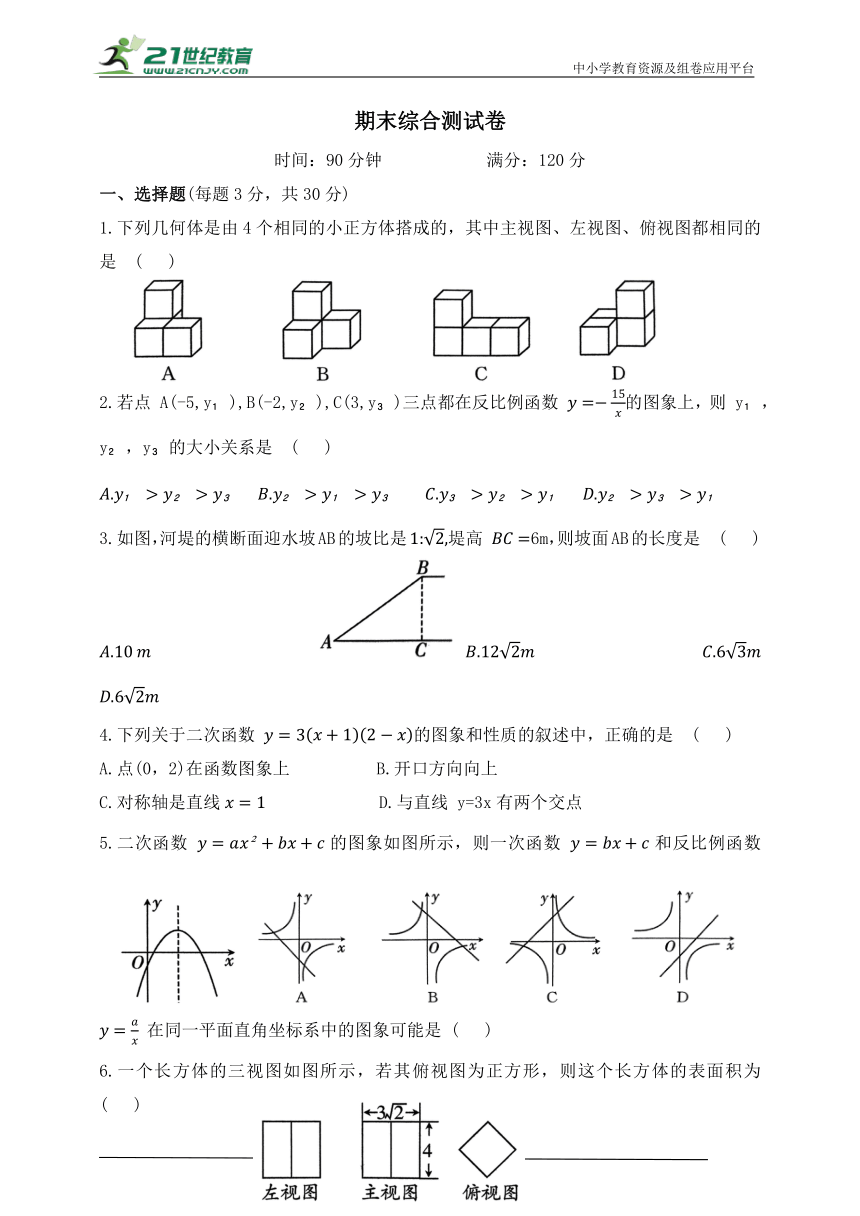
1.下列几何体是由4个相同的小正方体搭成的，其中主视图、左视图、俯视图都相同的是 ( )
2.若点 A(-5,y ),B(-2,y ),C(3,y )三点都在反比例函数 的图象上，则 y ，y ，y 的大小关系是 ( )
3.如图，河堤的横断面迎水坡AB的坡比是堤高 6m，则坡面AB的长度是 ( )
4.下列关于二次函数 的图象和性质的叙述中，正确的是 ( )
A.点(0，2)在函数图象上 B.开口方向向上
C.对称轴是直线 D.与直线 y=3x有两个交点
5.二次函数 的图象如图所示，则一次函数 和反比例函数 在同一平面直角坐标系中的图象可能是 ( )
6.一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的表面积为 ( )
A. 66 B. 48 D. 57
7.如图，在正方形网格中，△ABC按如图所示的位置摆放,则 cos∠ABC的值是 ( )
B.1
第7题图 第8题图
8.如图，已知反比例函数 的图象如图所示，将该曲线绕点O顺时针旋转 得到曲线 点 N 是曲线 上一点，点M在直线 上,连接MN,ON,若 的面积为 则 k 的值为 ( )
9.如图,在中，BC边上的高为3,点 D,E,F分别在边BC,AB,AC上,且∥
设点 E 到BC 的距离为x, 的面积为y，则y关于x的函数图象大致是 ( )
10.已知二次函数 的图象如图所示,下列5个结论:.其中正确的结论有 ( )
A. 5个 B. 4个 C. 3个 D. 2个
二、填空题(每题3分，共18分)
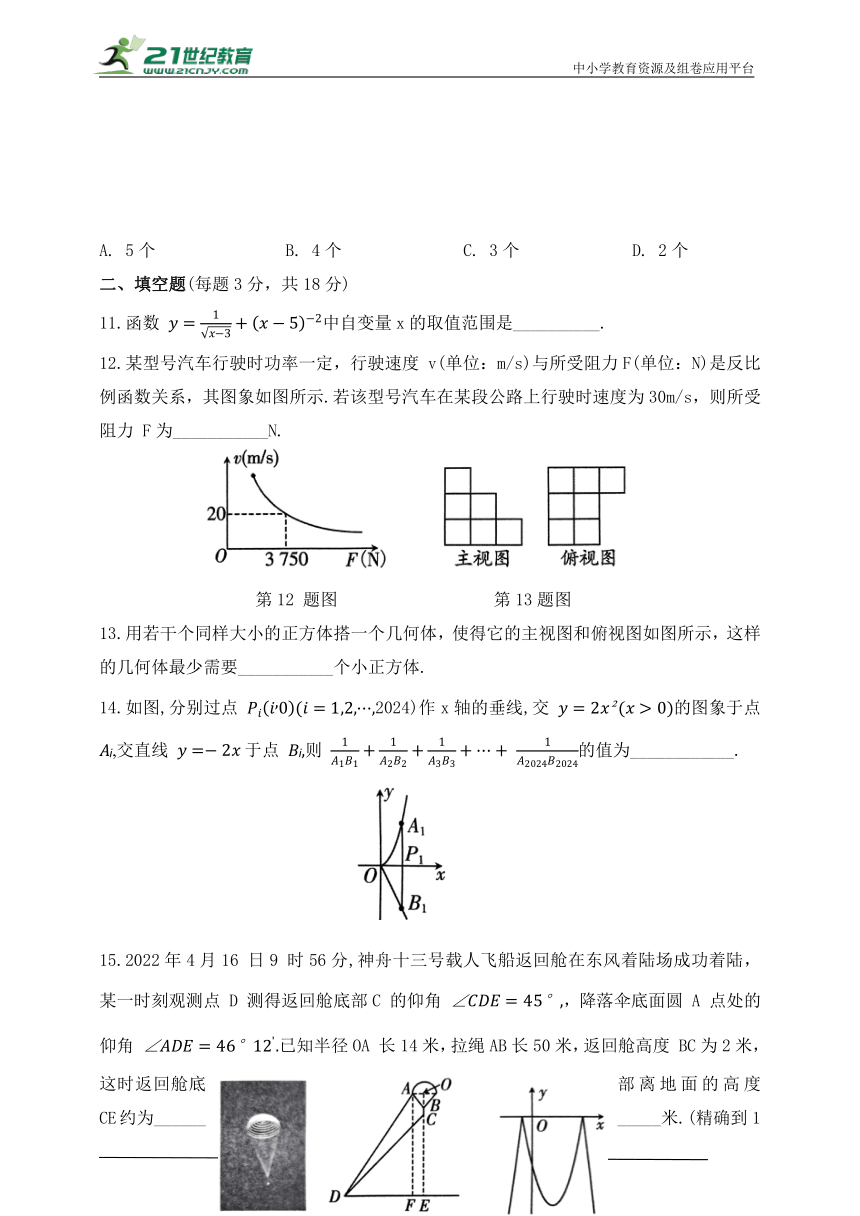
11.函数 中自变量x的取值范围是__________.
12.某型号汽车行驶时功率一定，行驶速度 v(单位：m/s)与所受阻力F(单位：N)是反比例函数关系，其图象如图所示.若该型号汽车在某段公路上行驶时速度为30m/s，则所受阻力 F为___________N.
第12 题图 第13题图
13.用若干个同样大小的正方体搭一个几何体，使得它的主视图和俯视图如图所示，这样的几何体最少需要___________个小正方体.
14.如图,分别过点 2024)作x轴的垂线,交 的图象于点 ,交直线 于点 则 的值为____________.
15.2022年4月16 日9 时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆，某一时刻观测点 D 测得返回舱底部C 的仰角 ，降落伞底面圆 A 点处的仰角 已知半径OA 长14米，拉绳AB长50米，返回舱高度 BC为2米，这时返回舱底部离地面的高度CE约为___________米.(精确到1米；参考数据：
第15 题图 第16 题图
16.已知二次函数 及一次函数 将该二次函数在x轴上方的图象沿x轴翻折到x 轴下方，图象的其余部分不变，得到一个新图象(如图所示)，当直线 与新图象有4个交点时，b的取值范围是____________.
三、解答题(共72分)
17.(6分)计算:
18.(8分)]我们在物理学科中学过：光线从空气射入水中会发生折射现象(如图1)，我们把 称为折射率(其中α代表入射角，β代表折射角).
观察实验：为了观察光线的折射现象，设计了图2 所示的实验，利用激光笔MN发射一束红光，容器中不装水时，光斑恰好落在 B处，加水至EF处，光斑左移至C处.图3是实验的示意图，四边形 ABFE为矩形，测得
(1)求入射角α的度数；
(2)若光线从空气射入水中的折射率 求光斑移动的距离 BC.(参考数据：
19.(8分)随着5G技术的进步与发展，生活中的测量技术也与时俱进.小颖与家人到经开区九寨山公园游玩时想用无人机测量公园内A，B两点之间的距离(A，B位于同一水平地面上)，如图所示，小颖站在A 处遥控空中C 处的无人机，此时她的仰角为α，无人机的飞行高度为81.5m，并且无人机C测得湖岸边B 处的俯角为( 若小颖的身高. (点A,B,C,D在同一平面内).求A，B两点之间的距离.(结果精确到
20.(8分)在平面直角坐标系中，已知一次函数 与坐标轴分别交于 A(5,0), 两点，且与反比例函数 的图象在第一象限内交于P，K两点，连接OP， 的面积为
(1)求一次函数与反比例函数的表达式；
(2)当 时，求x的取值范围；
(3)若点 C 为线段OA 上的一个动点，当 最小时，求 的面积.
21.(10分)世界杯足球赛期间，某商店销售一批足球纪念册，每本进价40元，规定销售单价不低于44 元，且获利不高于30%.试销售期间发现，当销售单价定为44元时，每天可售出300本，销售单价每上涨1元，每天销售量减少10本，现商店决定提价销售.设每天销售量为 y本，销售单价为x元.
(1)请直接写出y与x 之间的函数关系式和自变量x的取值范围；
(2)当每本足球纪念册销售单价是多少元时，商店每天获利2400元
(3)将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润w元最大 最大利润是多少元
22.(10分)小华想利用太阳光测量楼AB 的高，他带着尺子来到楼下，发现地面和对面斜坡(坡角为 上都有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：先测得在此时刻1.2m高的物体垂直于地面放置时，影长是1mm；楼AB 落在地面上的影长. 20m，落在斜坡上的影长 请你帮小华求出楼AB 的高.(结果保留根号)
23.(10分)某加工厂要加工一种抛物线形钢材构件，如图所示，该抛物线形构件的底部宽度米，顶点 P 到底部OM 的距离为9米.将该抛物线放入平面直角坐标系中，点M 在x轴上.其内部支架有两个符合要求的设计方案：
方案一是“川”字形内部支架(由线段AB,PN,DC构成),点 B,N,C在OM 上,且 ,点 A,D在抛物线上,AB,PN,DC均垂直于OM；
方案二是“H”形内部支架(由线段 EF 构成),点 在OM上,且 点 在抛物线上， 均垂直于OM,E,F 分别是 的中点.
(1)求该抛物线的函数表达式；
(2)该加工厂要用某一规格的钢材来加工这种构件，那么哪一个方案的内部支架节省材料 请说明理由.
24.(12分)如图,二次函数 的图象与x轴相交于点 A 和点C(1,0),交 y轴于点 B(0,3).
(1)求此二次函数的表达式；
(2)设二次函数图象的顶点为 P，对称轴与x轴交于点Q，求四边形AOBP 的面积；(请在图1中探索)
(3)二次函数图象的对称轴上是否存在点 M，使得△AMB 是以AB 为底边的等腰三角形 若存在，请求出满足条件的点 M 的坐标；若不存在，请说明理由.(请在图2中探索)
参考答案
1. A 2. B 3. C 4. D 5. D 6. A 7. D
8. B 解析:∵将直线 y=-x 逆时针旋转 后与x轴重合，曲线 绕点O逆时针旋转 后与 重合，∴旋转后点 N 落在曲线( 上，点M落在x轴上，如图所示，
设点 M 和点 N 的对应点分别为点. 和 过点 作 轴于点 P，连接
9. A 解析:过点 A 作 于点 H,交 EF于点 P.
∥ 即 解得
则 的面积
∴y关于x的函数图象是一个开口向下、顶点坐标为 的抛物线.
10. D
11. x>3且x≠5 12. 2500 13.10
解析： 由题 意，得
15.1614
解析：如图所示：
当y=0时, 5 = 0,解得 则 A(-1,0),B(5,0).
将该二次函数在 x轴上方的图象沿x轴翻折到x轴下方的部分图象的表达式为
①当直线 y=-x+b经过点A(-1,0)时,1+b=0,解得b=-1;
②当直线 y=-x+b与抛物线 5(-1≤x≤5)相切时,方程 -x+b,即 有两个相等的实数解，即 解得
所以，当直线y=-x+b与新图象有4个交点时，b的取值范围为
17.解:原式
18.解:(1)如图1,设法线为 与AB交于点H，则∥
∴∠α=∠BDN'=∠DBF=∠PDM',
∵BF=24 cm,DF=32 cm,
∴入射角约为53°，∴α=53°;
作DH⊥AB,
设CH=3x,CD=5x,则DH=4x,∴4x=24,解得x=6,
∴CH=18 cm,又∵BH=DF=32 cm,∴BC=BH-CH=32-18=14 cm,
所以，光斑移动的距离是 14 cm.
19.解:过点 C 作 CE⊥AB 交 AB 于点 E,作DF⊥CE 交CE 于点 F,
由题意,得 CE=81.5 m,AD⊥AB,∠ABC=60°,
∵AD⊥AB,CE⊥AB,DF⊥CE,∴∠DAE=∠AEF=∠EFD=90°,∴ 四 边 形 ADFE 是矩形，
∴EF=AD,DF=AE,
∵AD=1.5m,∴EF=1.5m,∴CF=CE-EF=81.5-1.5=80 m,
∵在 Rt△CDF中,CD=100m,CF=80 m,∴DF=60m,∴AE=60m,
∵在 Rt△CEB中,CE=81.5m ,∠ABC=60°,
∴AB=AE+BE=60+48=108(m),所以，A，B两点之间的距离为108 m.
20.解:(1)∵一次函数 与坐标轴分别交于A(5,0), 两点，
解得 ∴一次函数的表达式为
∵△OAP 的面积为
∵点 P 在一次函数图象上，∴令 解得
∵点 P 在反比例函数 的图象上，
∴一次函数的表达式为 反比例函数的表达式为
(2)令 解得 或 ∴K(1,2),
由图象，得当 时，x的取值范围为04;
(3)如图，作点 P 关于x 轴的对称点 连接KP',PC,线段 与x轴的交点即为点C，且此时 最小，
∴直线 的表达式为
令 解得
∴当 最小时， 的面积为
21.解:(1)由题意,得. 即
(2)由题意,得( 2400,
解得 (舍去),
所以，当每本足球纪念册销售单价是 50 元时，商店每天获利2 400元；
当 时，ω随x的增大而增大，而
所以当 时，w有最大值，最大值为
答：将足球纪念册销售单价定为52 元时，商店每天销售纪念册获得的利润w最大，最大利润是2 640元.
22.解:如图,过点 C 作 于点 M，作于点N.
则四边形 AMCN 是矩形，
∵测得在此时刻1.2m高的物体垂直于地面放置时，影长是1m，
即 解得
则 所以，楼AB 的高为
23.解：(1)∵该抛物线形构件的底部宽度 12米，顶点 P 到底部OM 的距离为9米，
∴顶点 P 的坐标为 P(6,9),点 O 的坐标为O(0,0),点 M 的坐标为M(12,0),
设抛物线的表达式为 将点O(0,0)的代入,解得
∴该抛物线的函数表达式为 即
(2)方案二的内部支架节省材料.理由：
方案一： 米， 米,OC=9米,
当x=3时, 即米，
当x=9时, 即米，
∴方案一内部支架材料长度为 (米);
方案二： 米，米， 米， 米，
当x=4时, 即 米，
当x=8时, 即 米，
∴方案二内部支架材料长度为 (米),
∴方案二的内部支架节省材料.
24.解:(1)由题意,得
(2)如图,连接OP,
令 得 ∴OA=3,
(3)设
由 得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑