资源简介

(共44张PPT)
第九章 平面直角坐标系
9.1 用坐标描述平面内点的位置
9.1.1 平面直角坐标系的概念
目
录
1. 学习目标
4. 知识点1 平面直角坐标系
7. 课堂小结
8. 当堂小练
CONTENTS
3. 新课导入
5. 知识点2 用坐标描述点的位置
10. 拓展与延伸
6. 知识点3 点的位置与点的坐标的关系
9. 对接中考
2. 知识回顾
1. 理解平面直角坐标系的概念，能画出平面直角坐标系，提升抽象能力， 增强动手能力.
2. 在平面直角坐标系中，能由点的位置确定点的坐标或能由点的坐标确定点的位置.
学习目标
知识回顾
有序数对
用含有两个数的表达方式来表示一个确定的位置，其中两个数各自表示不同的含义.我们把这种有顺序的两个数 a 与 b 组成的数对，叫做有序数对. 记作(a，b).
实数和数轴上的点一一对应：
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数.
新课导入
【问题】在庆祝中华人民共和国成立70周年联欢活动中，天安门广场上出现了“祖国万岁”等壮观的图案，你知道它们是怎么组成的吗
表演现场设置了由有序数对标识的点位，3 000多名表演者手举光影屏，根据预先编排的流程，不停地变换所在的点位，就拼出了不同的图案.
类似于生活中用有序数对确定位置，在数学中可以通过建立平面直角坐标系，用坐标来刻画平面内点的位置.
新课讲解
知识点1 平面直角坐标系
数轴上的点与实数是一一对应的，数轴上每个点都对应一个实数，这个实数叫作这个点在数轴上的坐标.
1. 在图中的数轴上，点A、点B的坐标分别是多少？
点A的坐标为-4，点B的坐标为2.
0
1
2
3
4
-3
-2
-1
A
B
C
5
-4
2. 反过来，利用数轴上点的坐标，可以确定直线上点的位置.坐标为5的点在哪？
是点C.
新课讲解
类似于利用数轴确定直线上点的位置，能不能找到一种办法来确定平面内的点的位置呢(例如图中A，B，C，D，E各点)
A
B
C
D
E
新课讲解
我们可以在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系.
水平的数轴称为x轴或横轴，习惯上取向右为正方向；
竖直的数轴称为y轴或纵轴，习惯上取向上为正方向；
两坐标轴的交点O称为平面直角坐标系的原点.
x
y
O
横轴
纵轴
原点
取向右为正方向
取向上为正方向
新课讲解
1.平面直角坐标系的两条数轴共原点，且互相垂直.
2.一般情况下，两坐标轴的单位长度是一致的，在有些实际问题中，两坐标轴的单位长度可以不同，但在同一坐标轴上的单位长度必须相同.
注意
新课讲解
例
1. 下列四个选项中，关于平面直角坐标系的画法正确的是（ ）
D
两条数轴不垂直
x 轴上
数字错误
两条数轴
没有正方向
新课讲解
练一练
下列关于平面直角坐标系的说法正确的是( )
A. 由两条共原点的数轴构成
B. 由两条垂直的数轴构成
C. 正方向没有规定
D. 两坐标轴的单位长度可以不同
D
新课讲解
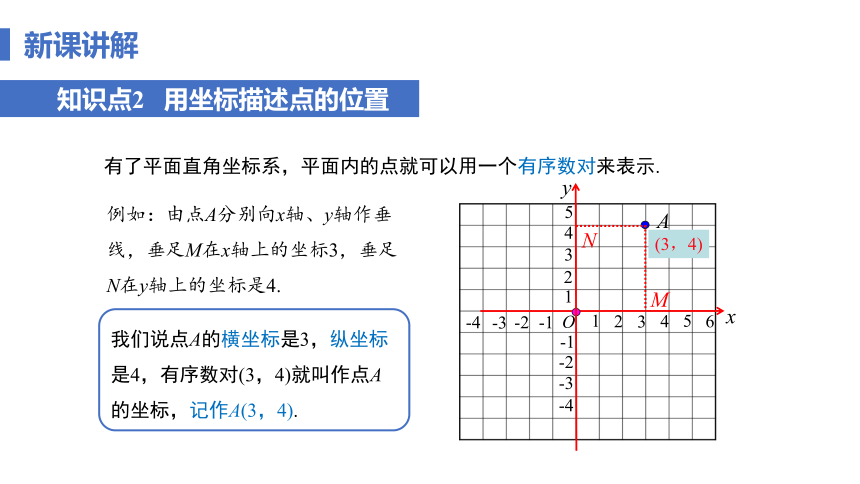
知识点2 用坐标描述点的位置
例如：由点A分别向x轴、y轴作垂线，垂足M在x轴上的坐标3，垂足N在y轴上的坐标是4.
有了平面直角坐标系，平面内的点就可以用一个有序数对来表示.
2
-1
A
1
5
4
3
-4
-3
-2
-1
O
6
4
3
2
1
5
-2
-3
-4
x
y
(3，4)
N
M
我们说点A的横坐标是3，纵坐标是4，有序数对(3，4)就叫作点A的坐标，记作A(3，4).
新课讲解
【定义】若平面直角坐标系中有一点 A，过点 A 作横轴的垂线，垂足在横轴上表示的数为 a，过点 A 作纵轴的垂线，垂足在纵轴上表示的数为 b，则有序实数对（a， b）叫作点 A的坐标，其中 a 叫作横坐标， b 叫作纵坐标 .
新课讲解
类似地，你能写出点 B，C，D的坐标吗？
B (3，4)
C (0，2)
D (0，3)
x
O
y
1 2 3 4
4 3 2 1
4
3
2
1
1
2
3
4
1. 在写点的坐标时，必须先写横坐标，再写纵坐标，中间用逗号隔开，最后用小括号把它们括起来.
2. 点的坐标是有序实数对， (a，b)和(b，a) (a≠ b)虽然数字相同，但由于顺序不同，表示的位置就不同.
注意
新课讲解
你能在图中找到坐标为(3，2)的点吗？
由坐标找点的方法
(1) 先在坐标轴上找到表示横坐标与纵坐标的点；
(2) 然后过这两点分别作轴与轴的垂线；
(3) 垂线的交点就是该坐标对应的点.
x
O
y
1 2 3
4 3 2 1
4
3
2
1
1
2
3
新课讲解
2. 在平面直角坐标系中描出下列各点：
A(4，5)，B(-2，3)，C(-2.5，-2)，
D(4，-2)，E(0，-4).
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
A(4，5)
B(-2，3)
C(-2.5，-2)
D(4，-2)
E(0，-4)
解：如图，先在x轴上找出表示4的点，再在y轴上找出表示5的点，过这两个点分别作x轴和y轴的垂线，垂线的交点就是点A.
类似地，可在图中描出点B，C，D，E.
例
新课讲解
2
-1
A
1
5
4
3
-4
-3
-2
-1
O
6
4
3
2
1
5
-2
-3
-4
x
y
(3，4)
N
M
点到坐标轴的距离：
若点A(a，b)，
则点A到x轴的距离为点A的纵坐标的绝对值，即为|b|；
点A到y轴的距离为点A的横坐标的绝对值，即为|a|.
新课讲解
练一练
在如图所示的平面直角坐标系中，
(1)写出A，B，C三点的坐标;
(2)描出点D(2，-3)，E(-2，4)，F(0，-2)；
(3)分别写出点A，B，C到x轴、y轴的距离.
解：(1) A(4，3)，B(-3，0)，C(-4，-1).
(2) 如图所示.
点 到x轴的距离 到y轴的距离
A
B
C
(3)
3
4
0
3
1
4
新课讲解
知识点3 点的位置与点的坐标的关系
【思考】原点O的坐标是什么 x轴和y轴上的点的坐标有什么特点
原点O的坐标为(0，0)；
x轴上的点：(1，0)，(-1，0)…；
y轴上的点的： (0，1)，(0，-1)….
2
-1
1
5
4
3
-4
-3
-2
-1
O
6
4
3
2
1
5
-2
-3
-4
x
y
x轴上的点的纵坐标为0，
y轴上的点的横坐标为0.
新课讲解
建立平面直角坐标系以后，坐标平面就被两条坐标轴分成Ⅰ，Ⅱ，Ⅲ，Ⅳ四个部分，每个部分称为象限.
象限
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
坐标轴上的点属于哪个象限？
坐标轴上的点不属于任何象限.
新课讲解
【思考】每个象限内点的坐标符号具有什么特点？
（＋，＋）
（－，＋）
（－，－）
（＋，－）
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上
在y轴上
＋
＋
－
＋
－
－
＋
－
纵坐标为0
横坐标为0
新课讲解
点（ a， b）的位置 横、纵坐标的符号特点 图示
在 象 限 内 第一象限 （+，+），即 a ＞ 0， b ＞ 0
第二象限 （-，+），即 a ＜ 0， b ＞ 0
第三象限 （-，-），即 a ＜ 0， b ＜ 0
第四象限 （+，-），即 a ＞ 0， b ＜ 0
在 坐 标 轴 上 x轴 正半轴 （+，0），即 a ＞ 0， b0
负半轴 （-，0），即 a ＜ 0， b0
y轴 正半轴 （0，+），即 a0， b ＞ 0
负半轴 （0，-），即 a0， b ＜ 0
原点 （0，0），即 a0， b0
横、纵坐标的符号
共同决定点所在象限
原点既在 x 轴上，
又在 y 轴上
归纳
新课讲解
例
3. 如图，坐标平面上有 A、B、C、D 四点．根据图中各点位置判断，哪一个点在第二象限（　　）
A．A B．B C．C D．D
A
新课讲解
例
3. 在平面直角坐标系中，点M(m-3，m+1)在x轴上，则点P(m-1，1-m)在 (　　)
B
A.第一象限 B.第二象限
C.第三象限 D.第四象限
纵坐标为0
m=-1
P(-2，2)
新课讲解
例
4. 已知平面直角坐标系内的不同两点A(3，a－1)，B(b＋1，－2).
(1)若点A 在第一、三象限的角平分线上，求a 的值；
(2)若点B 在第二、四象限的角平分线上，求b 的值；
(3)若直线AB 平行于y 轴，且AB=5，求a，b 的值.
解：(1) ∵点A 在第一、三象限的角平分线上，
∴ a－1=3，
∴ a=4.
(2) ∵点B 在第二、四象限的角平分线上，
∴ b＋1=2，
∴ b=1.
(3) ∵直线AB 平行于y 轴，且AB=5，
∴ b＋1=3，|(a－1)－(－2)|=5.
∴ b=2，a=4 或a=－6.
新课讲解
归纳
点的位置 点的横、纵坐标的关系
在角平分线上 在第一、三象限的角平分线上 相等
在第二、四象限的角平分线上 互为相反数
在平行于坐标轴的直线上 在平行于 x 轴的直线上 纵坐标相等
在平行于 y 轴的直线上 横坐标相等
若两个点的横坐标相同，则这两个点之间的距离为纵坐标差的绝对值；若两个点的纵坐标相同，则这两个点之间的距离为横坐标差的绝对值 .
注意
新课讲解
练一练
1. 下列说法错误的是(　　 )
A．平面内两条互相垂直的数轴就构成了平面直角坐标系
B．平面直角坐标系中两条数轴是互相垂直的
C．坐标平面被两条坐标轴分成了四个部分，每个部分称为象限
D．坐标轴上的点不属于任何象限
A
新课讲解
练一练
2. 在平面直角坐标系中，已知点M(m-2，2m-7).
(1)若点 M 在 x 轴上，求 m 的值和点 M 的坐标；
(2)若点 M 在 y 轴上，求 m 的值和点 M 的坐标 .
解：(1) ∵ 点 M 在 x 轴上，
∴ 2m-7=0，解得 m= .
∴ m-2= -2= .
∴ M（ ，0） .
(2)∵ 点 M 在 y 轴上，
∴ m-2=0，解得 m=2.
∴ 2m-7 ＝ 2× 2-7=-3.
∴ M（0， -3） .
新课讲解
练一练
3. 若|a|=5，b2=16，且点M(a，b)在第三象限，则点M的坐标是(　　)
C
A.(5，4)
B.(-5，4)
C.(-5，-4)
D.(5，-4)
a=±5，b=±4
a=-5， b=-4
新课讲解
练一练
4. 已知平面直角坐标系内的三点： A( a-1 ，- 2 ) ， B ( - 3 ，a+2)， C(b-6，2b).
(1)当直线 AB ∥ x 轴时，求 A， B 两点间的距离；
(2)当直线 AC ⊥ x 轴，点 C 在第二、四象限的角平分线上时，求点 A和点 C 的坐标．
解：(1) ∵直线AB∥x轴，
∴a＋2＝－2，解得a＝－4.
∴a－1＝－5.
∴A(－5，－2)，B(－3，－2)．
∴A，B两点间的距离为－3－(－5)＝2.
(2) ∵点C(b－6，2b)在第二、四象限的角平分线上，
∴b－6＋2b＝0，解得b＝2.
∴b－6＝2－6＝－4，2b＝2×2＝4.
∴点C的坐标为(－4，4)．
又∵直线AC⊥x轴，
∴A(－4，－2)．
新课讲解
对于坐标平面内任意一点M，都有唯一的坐标和它对应吗？
对于坐标平面内任意一点M，都有唯一的一个有序实数对(x，y)(即点M的坐标)和它对应；
反过来，对于任意一个有序实数对(x，y)，在坐标平面内都有唯一的一点M(即坐标为(x，y)的点)和它对应.
坐标平面内的点与有序实数对是一一对应的.
课堂小结
内点的位置
用坐标描述平面
象限点、x轴及y轴上点的坐标的特征：
第一象限：(+，+)，第二象限：(-，+)
第三象限：(-，-)，第四象限：(+，-)
x轴上的点的纵坐标为0，表示为(x，0)
y轴上的点的横坐标为0，表示为(0，y)
原点
象限
坐标轴
点的坐标特征
平面直角坐标系
4个象限
当堂小练
1. 请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上？
A（-5，2) B (3，-2） C（0，4） D（-6，0）
E（1，8） F（0，0） G（5，0） H（-6，-4)
M （0，-3）
第二象限
第四象限
y轴的正半轴上
x轴的负半轴上
第一象限
坐标原点
x轴的正半轴上
第三象限
y轴的负半轴上
当堂小练
2. 如图，在平面直角坐标系中，
(1) 写出 A，B，C 三点的坐标；
(2) 描出点 D (2，3)，E (2，4)，F (0，2).
x
O
y
1 2 3 4
4 3 2 1
4
3
2
1
1
2
3
B
C
D
A
(4，3)
(3，0)
(4，1)
E
F
当堂小练
3. 若点P（a，b）在第二象限，则点M（b－a，a－b）在（ 　　）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
D
当堂小练
4. 已知点 P 的坐标为(3a+6，2-a)，且点 P 到两坐标轴的距离相等，则点 P 的坐标是_______________.
(3，3)或(6，6)
|2a|=|3a+6|
a=1或a=4
2a=3a+6 或 2a=(3a+6)
(3，3)或(6，6)
当堂小练
5. 已知点 A(1，2)和点 B(3，m1)，如果直线 AB//x 轴，那么 m 的值为( )
A.1 B. 4 C. 1 D.3
C
点 A 和点 B 的纵坐标相等
2m1
m=1
当堂小练
6. 已知a+b>0，ab>0，则在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是( )
A.(a，b) B.(-a，b) C.(-a，-b) D.(a，-b)
解析：∵a+b>0，ab>0.
∴a>0，b>0.
∵小手盖住的点在第四象限，
∴该点的横坐标大于0，纵坐标小于0.
∴(a，-b)满足题意.
D
当堂小练
7. 已知点 M (3a9，a1).
(1) 若点 M 在 y 轴上，求点 M 的坐标；
(2) 若点 M 在第二、四象限的角平分线上，求点 M 的坐标；
(3) 若点 M 的纵坐标比横坐标大 4，求点 M 的坐标.
解：（1）∵ 点 M 在 y 轴上，
∴ 3a9=0，解得 a=3，
∴ a1=2，
∴ 点 M 的坐标为(0，2).
（2）∵ 点 M 在第二、四象限的角平分线上，
∴ 3a9+a1=0，解得 a=2.5，
∴ 3a9=1.5，a1=1.5，
∴ 点 M 的坐标为( 1.5，1.5).
（3）由题意可知，
a1(3a9)4，
解得 a2，
∴ 3a93，a1l，
∴ 点 M 的坐标为( 3，1).
对接中考
1. 在平面直角坐标系的第四象限内有一点 M ，到 x 轴的距离为 4，到 y 轴的距离为 5，则点 M 的坐标为（ 　　）
A.（4，5） B.（5，4）
C.（4，5） D.（5，4）
D
横坐标为正，纵坐标为负
纵坐标为4
横坐标为5
对接中考
2. 在平面直角坐标系中，点 P (x2+2，3) 所在的象限是（　 　）
A．第一象限
B．第二象限
C．第三象限
D．第四象限
D
x2+2>0
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
对接中考
3. 在平面直角坐标系中，若点A (a，b) 在第三象限，则点 B (ab，b) 所在的象限是（　　 ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
A
a<0，b>0
b>0
ab>0
对接中考
4. 如果单项式 -x2my3与单项式 2x4y2-n的和仍是一个单项式，则在平面直角坐标系中点（m， n）在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D
解：∵ 单 项 式 -x2my3与 单 项 式2x4y2-n的和仍是一个单项式，
∴ 单项式 -x2my3与单项式 2x4y2-n是同类项 .
∴ 2m=4，2-n=3，解得 m=2， n=-1.
∴ 点（m， n）在第四象限 .
拓展与延伸
如图 ，动点 P 在平面直角坐标系中按箭头所示方向运动，第 1 次从原点运动到点（1，1），第 2 次接着运动到点（2，0），第 3 次接着运动到点（3，2），第 4 次接着运动到点（4，0），…，按这样的运动规律，经过第 2025 次运动后，动点 P 的坐标是__________ .
（2 025，1）
解：根据图所示的点P的坐标变化规律，可以看出：①点P运动后的横坐标依次为1，2，3，4，…，即点P的横坐标等于运动的次数，所以经过第2025次运动后，点P的横坐标是2025；
②点P运动后的纵坐标依次是1，0，2，0，1，0，2，0，…，即每运动 4 次为一个循环 . 因为2 025÷4=506 …… 1，所以经过第 2 025 次运动后，点 P 的纵坐标与经过第 1 次运动后的纵坐标相同，为 1. 所以经过第 2 025 次运动后，点 P 的坐标是（2 025，1） .

展开更多......

收起↑