资源简介

第四章 三角形 复习课
【复习目标】
1.知道三角形的相关概念、边角关系以及性质.
2.总结三角形不同的判定条件,会利用尺规作全等三角形.
3.会构建全等三角形,能应用三角形全等解决相关实际问题.
【重点】
三角形全等的判定条件.
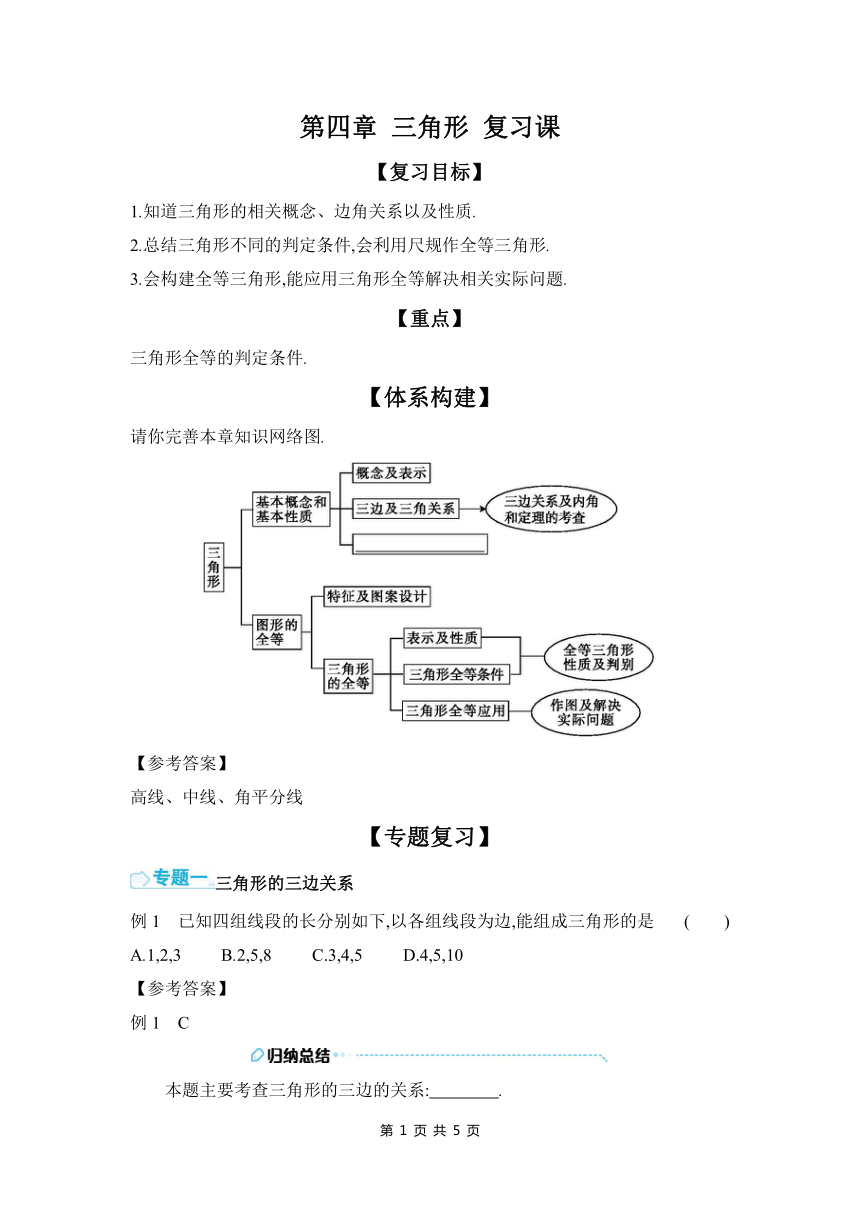
【体系构建】
请你完善本章知识网络图.
【参考答案】
高线、中线、角平分线
【专题复习】
三角形的三边关系
例1　已知四组线段的长分别如下,以各组线段为边,能组成三角形的是 (　　)
A.1,2,3 B.2,5,8 C.3,4,5 D.4,5,10
【参考答案】
例1　C
　　本题主要考查三角形的三边的关系:　　　　.
【参考答案】
归纳总结　三角形的两边之和大于第三边
变式训练
下列长度的三条线段,不能组成三角形的是 (　　)
A.3,8,4 B.4,9,6
C.15,20,8 D.9,15,8
【参考答案】
　A
三角形的三个内角关系
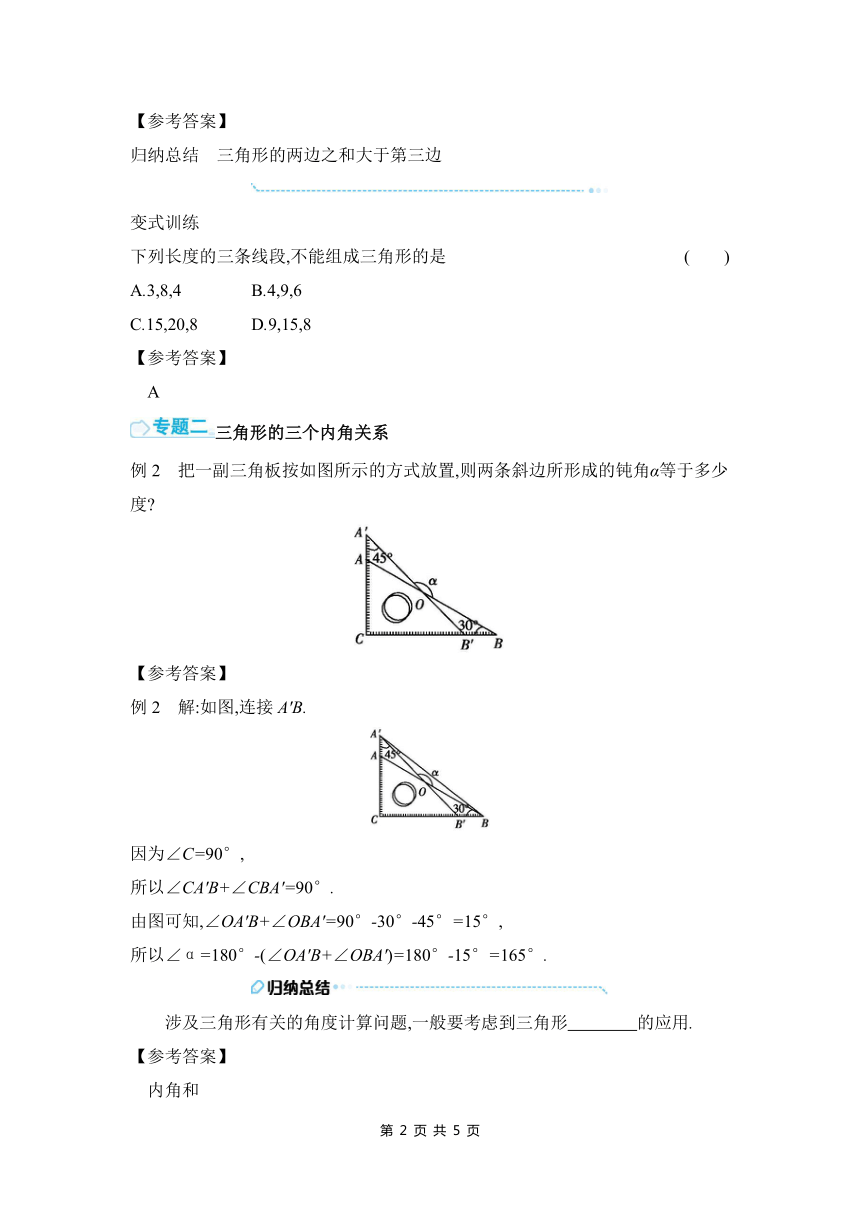
例2　把一副三角板按如图所示的方式放置,则两条斜边所形成的钝角α等于多少度
【参考答案】
例2　解:如图,连接A'B.
因为∠C=90°,
所以∠CA'B+∠CBA'=90°.
由图可知,∠OA'B+∠OBA'=90°-30°-45°=15°,
所以∠α=180°-(∠OA'B+∠OBA')=180°-15°=165°.
　　涉及三角形有关的角度计算问题,一般要考虑到三角形　　　　的应用.
【参考答案】
　内角和
变式训练
如图,在△ABC中,∠A=80°,D是BC延长线上的一点,∠ACD=150°,则∠B=　　　　.
【参考答案】
70°
三角形的分类及三角形中的三条重要线段
例3　如图,在△ABC中,分别画出它的中线AD和高AE,并回答下列问题:
(1)AE还是哪些三角形的高
(2)△ABD与△ACD的面积有什么关系 为什么
【参考答案】
例3　解:(1)如
图,AE还是△ABD、△ADE、△ADC、△AEC、△ABE的高.
(2)△ABD与△ACD的面积相等,因为这两个三角形等底同高.
全等三角形的性质与判定
例4　如图,一张矩形纸片沿对角线剪开(如图1)得到两张三角形纸片(如图2),再将这两张三角形纸片摆成如图3所示的形式,使点B,F,C,D在同一直线上.
(1)试说明AB⊥ED.
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并证明.
【参考答案】
例4　解:(1)由题意得∠A+∠B=90°,∠A=∠D,
所以∠D+∠B=90°,所以AB⊥DE.
(2)若PB=BC,则有Rt△ABC≌Rt△DBP.
证明:因为∠B=∠B,∠A=∠D,BC=BP,
所以Rt△ABC≌Rt△DBP(AAS).
用尺规作三角形
例5　如图,求作一个边长为a的等边三角形.
变式训练
已知:如图,线段a,c,∠α.
求作:△ABC,使得BC=a,AB=c,∠ABC=∠α.
【参考答案】
例5　
解:已知线段a,求作△ABC,使AB=AC=BC=a.
作法:如图,(1)作线段BC=a;(2)分别以B,C为圆心,以a的长为半径画弧,两弧交于点A;(3)连接AB,AC,△ABC为所求作的等边三角形.
变式训练
解:如图.
用全等三角形测距离
例6　公园里有一条“Z”字形道路ABCD,如图,其中AB∥CD,在AB、BC、CD三段路上各有一只石凳E、M、F,M恰好为BC的中点,且E、F、M在同一直线上,在BE道路中停放着一排小汽车,从而无法直接测量B,E之间的距离,你能想出解决的方法吗 请说明其中的道理.
【参考答案】
例6　
解:能.连接E,F,M.
因为AB∥CD,所以∠B=∠C.
因为M为BC的中点,
所以BM=MC.
因为∠EMB=∠FMC,
所以△EBM≌△FCM,所以BE=CF.

展开更多......

收起↑