资源简介

第9章 轴对称、平移与旋转 复习课
【素养目标】
1.知道图形经过轴对称、平移、旋转后得到一个与原图形全等的图形.
2.会画简单的几何图形轴对称、平移、旋转后的图形,增强欣赏生活中的数学美的能力.
3.会用轴对称、平移、旋转、全等的性质解决简单的数学问题.
【重点】
轴对称、平移、旋转、全等的性质.
【体系构建】
【专题复习】
轴对称图形及性质
例1　下列四个图案中,可以看作是轴对称图形的是 ( )
　　　
A　　　　B　　　　C　　　　D
变式训练
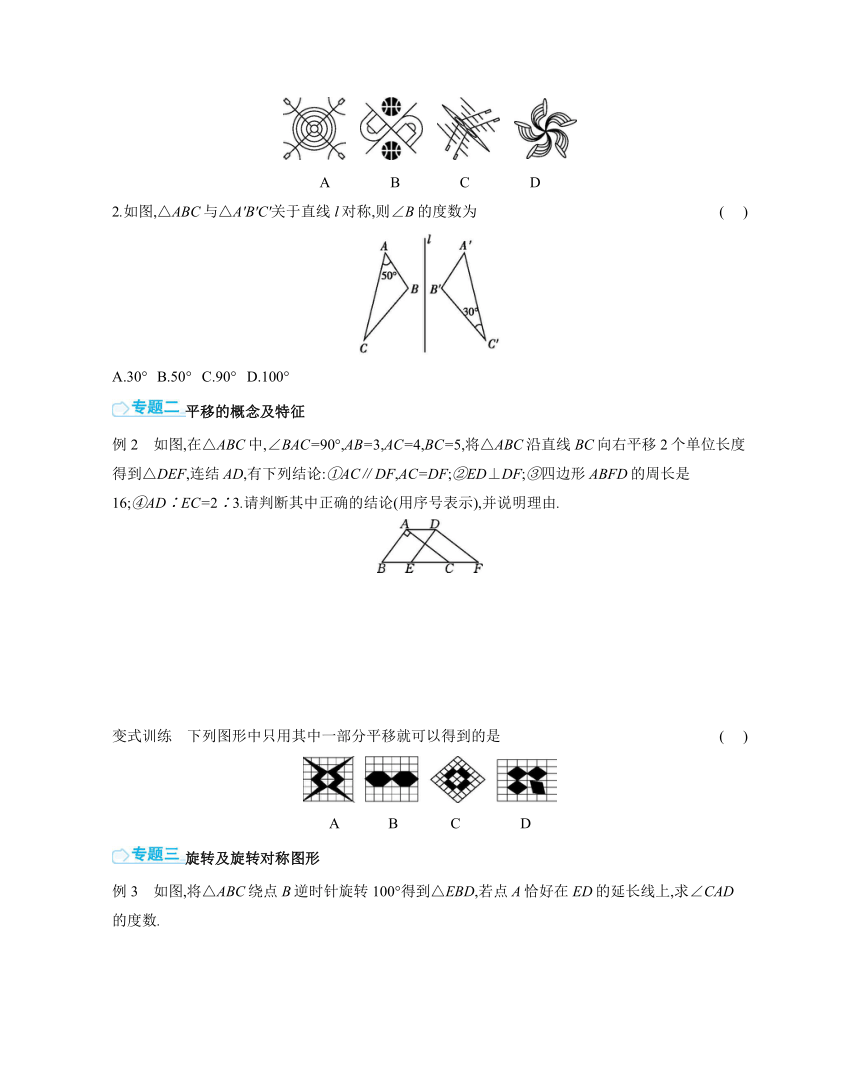
1.第33届夏季奥林匹克运动会于2024年7月26日在巴黎开幕,此次奥运会体育项目图标含有图形变换的元素.下列分别是射箭、篮球、赛艇、冲浪项目的图标,其中是轴对称图形但不是中心对称图形的是 ( )
　　　
A　　　　B　　　　C　　　　D
2.如图,△ABC与△A'B'C'关于直线l对称,则∠B的度数为 ( )
A.30° B.50° C.90° D.100°
平移的概念及特征
例2　如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位长度得到△DEF,连结AD,有下列结论:①AC∥DF,AC=DF;②ED⊥DF;③四边形ABFD的周长是16;④AD∶EC=2∶3.请判断其中正确的结论(用序号表示),并说明理由.
变式训练　下列图形中只用其中一部分平移就可以得到的是 ( )
A　 　　B　 　　 C　　　　D
旋转及旋转对称图形
例3　如图,将△ABC绕点B逆时针旋转100°得到△EBD,若点A恰好在ED的延长线上,求∠CAD的度数.
变式训练　如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕着点A旋转到△AED的位置,使得CD∥AB,则∠BAE等于 ( )
A.30° B.40° C.50° D.60°
中心对称
例4　下列图形中,既是轴对称图形又是中心对称图形的是 ( )
A　　　 　B　　　 　C　　　　D
变式训练　下列字母中,既是轴对称图形又是中心对称图形的是 ( )
　　　
A　　　　B　　　　C　　　　D
图形的全等
例5　如图,点B,E在CF上,且△ABC≌△DEF.若CF=12,BE=6,∠ABF=50°.
(1)求CE的长.
(2)求∠DEC的度数.
变式训练　如图,△ABC≌△ADE,∠BAD=52°.
(1)求∠EAC的度数.
(2)△ABC怎样运动能与△ADE重合
【参考答案】
专题一
例1　B
变式训练
1.C　2.D
专题二
例2　解:正确的结论为①②③④.
理由:∵将△ABC沿直线BC向右平移2个单位长度得到△DEF,
∴AD=BE=CF=2,AC∥DF,AB∥DE,AB=DE=3,AC=DF=4,BC=EF=5,∠BAC=∠EDF=90°,
∴BF=5+2=7,EC=5-2=3,DE⊥DF,∴①和②都正确.
∵四边形ABFD的周长=AB+AD+DF+BF=3+2+4+7=16,∴③正确.
∵AD=2,EC=3,∴AD∶EC=2∶3,∴④正确.
∴正确的结论为①②③④.
变式训练　B
专题三
例3　解:根据旋转的特征得∠CBD=100°,∠ACB=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°.
∵∠ADB+∠DBC+∠ACB+∠CAD=360°,
∴180°+100°+∠CAD=360°,∴∠CAD=80°.
变式训练　B
专题四
例4　B
变式训练　D
专题五
例5　解:(1)∵△ABC≌△DEF,
∴BC=EF,
∴BC-BE=EF-BE,∴CE=FB.
∵CF=12,BE=6,∴FB+6+CE=12,
∴CE=3.
(2)∵∠ABF=50°,∴∠ABC=180°-50°=130°.
∵△ABC≌△DEF,∴∠ABC=∠DEF=130°,
∴∠DEC=180°-130°=50°.
变式训练　解:(1)因为△ABC≌△ADE,
所以∠BAC=∠DAE,
所以∠BAC-∠BAE=∠DAE-∠BAE,
所以∠EAC=∠BAD=52°.
(2)△ABC绕点A顺时针旋转52°能与△ADE重合.

展开更多......

收起↑