资源简介

中小学教育资源及组卷应用平台
一次函数
专题讲练1 一次函数图象及性质
考点一 待定系数法【典例1】弹簧原长(不挂重物)12 cm，弹簧总长L(cm)与重物质量x(kg)的关系如表所示：
弹簧总长L(cm) 13 14 15 16 17
重物质量x(kg) 0.5 1.0 1.5 2.0 2.5
当重物质量为7.5kg(在弹性限度内)时，弹簧的总长L(cm)是( )
A.27 B.27.5 C.20 D.19.5
变式1.已知直线y= ax+b与直线y=x+3交于点B(-3,n),则代数式 的值为( )
A.0 B.1 C.2 D.3
变式2.若点A(x ,y ),点B(x ,y )为一次函数y=3x-1的图象上的两个不同的点,且 设 则M与N 的大小关系为()
A. M>N B. M变式3.某学习小组在网上获取了声音在空气中的传播速度和空气温度之间的关系的一些数据如表.下列说法中错误的是( )
温度(℃) -20 -10 0 10 20 30
声速(m/s) 318 324 330 336 342 348
A.温度每降低10℃,声速减少6m /s
B.若想让声速为355 m/s,则温度应为 40 ℃
C.当温度升高到33 ℃时,声速为349.8 m/s
D.在这个变化过程中，自变量是温度，声速是温度的函数
【典例2】若一次函数y=(2m-3)x+m-1图象不过第三象限，则m取值范围为( )
变式.已知直线y=(k-2)x+1经过点A(a,y ),点B(a+1,y ),且. 则k 的取值范围是( )
A. k>2 B. k<2 C. k>0 D. k<0
考点： 直线的交点
【典例3】(2023·南充)如图,直线y= kx-2k+3(k为常数,k<0)与x,y轴分别交于点A，B，则 的值是 .
变式.(2022·北京)直线y=x+4,对于x<2时每一个x值,函数y= nx(n≠0)的值小于y=x+4|的值，求n 的取值范围.
专题讲练2 一次函数图象信息(一)——行程问题(1)
考点一 理解x 与y的含义，求解析式、解方程组、求交点坐标
【典例】(2021·武汉)一辆快车和一辆慢车将一批物资从甲地运往乙地，其中快车送达后立即沿原路返回，且往返速度的大小不变，两车离甲地的距离y(单位：km)与慢车行驶时间t(单位：h)的函数关系如图，则两车先后两次相遇的间隔时间是( )
A. B. c. D.
变式1.(2020·重庆)A,B 两地相距240 km,甲货车从A 地以40km/h的速度匀速前往 B地，到达B 地后停止，在甲出发的同时，乙货车从B 地沿同一公路匀速前往A 地，到达A 地后停止，两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线所示.其中点 C 的坐标是(0,240),点 D 的坐标是(2.4,0),则点 E 的坐标是 ·
考点二 行程问题核心看图求速度
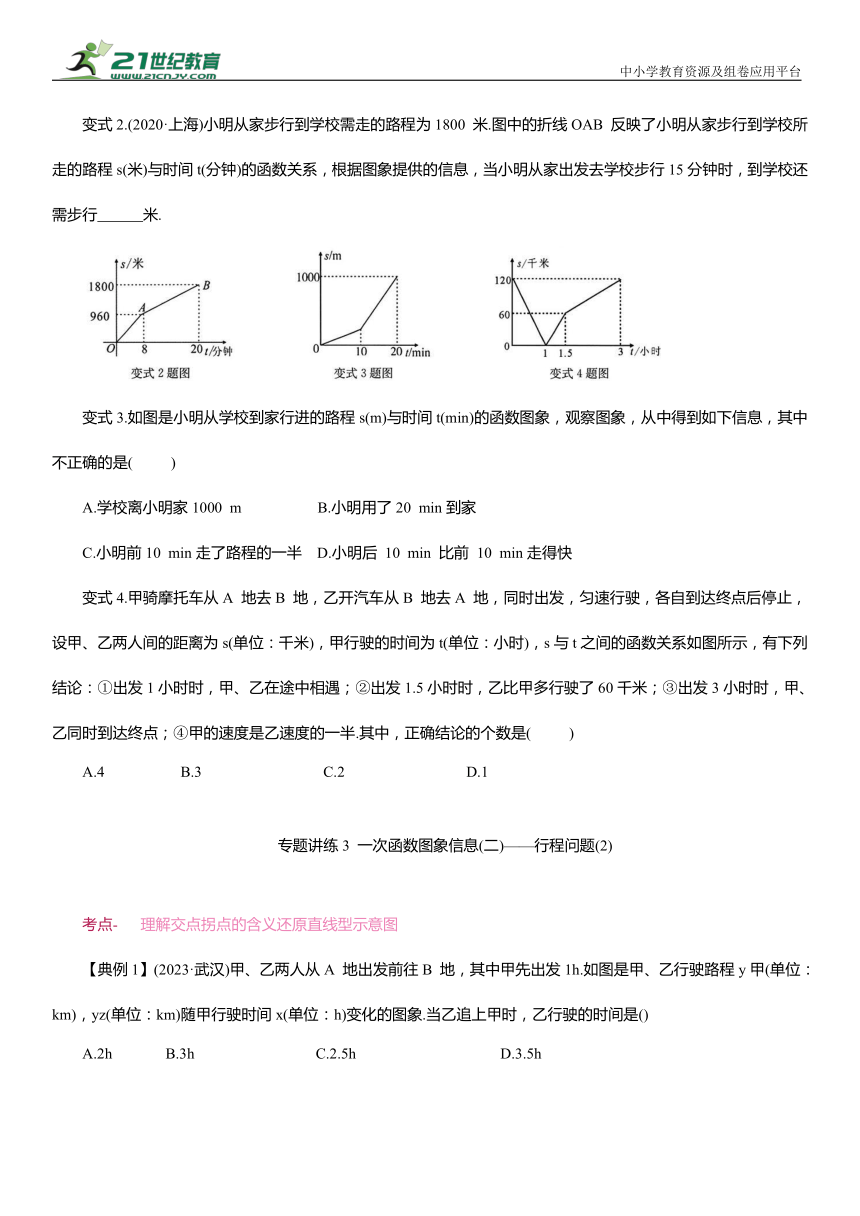
变式2.(2020·上海)小明从家步行到学校需走的路程为1800 米.图中的折线OAB 反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行 米.
变式3.如图是小明从学校到家行进的路程s(m)与时间t(min)的函数图象，观察图象，从中得到如下信息，其中不正确的是( )
A.学校离小明家1000 m B.小明用了20 min到家
C.小明前10 min走了路程的一半 D.小明后 10 min 比前 10 min走得快
变式4.甲骑摩托车从A 地去B 地，乙开汽车从B 地去A 地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间的距离为s(单位：千米)，甲行驶的时间为t(单位：小时)，s与t之间的函数关系如图所示，有下列结论：①出发1小时时，甲、乙在途中相遇；②出发1.5小时时，乙比甲多行驶了60千米；③出发3小时时，甲、乙同时到达终点；④甲的速度是乙速度的一半.其中，正确结论的个数是( )
A.4 B.3 C.2 D.1
专题讲练3 一次函数图象信息(二)——行程问题(2)
考点- 理解交点拐点的含义还原直线型示意图
【典例1】(2023·武汉)甲、乙两人从A 地出发前往B 地，其中甲先出发1h.如图是甲、乙行驶路程y甲(单位：km)，yz(单位：km)随甲行驶时间x(单位：h)变化的图象.当乙追上甲时，乙行驶的时间是()
A.2h B.3h C.2.5h D.3.5h
变式.小华上学，先步行后乘公共汽车到校，行程情况如图所示，小华恰好按规定时间到校，第二天骑自行车上学，平均速度是第一天步行的速度的4倍，若要按时到校，则从家出发的时间应比前一天出发的时间晚( )
A.5 min B.4m in C.3 min D.2m in
考点二 行程问题核心看图求速度
【典例2】(2020·武汉五调)小明从家出发去上学，先步行一段路，因时间紧，他改骑共享单车，结果到学校时迟到了7 min，其行驶的路程y(单位：m)时间x(单位：min)的图象关系如图.若他出门时直接骑共享单车(两次骑车速度相同)，则下列说法正确的是( )
A.小明会迟到2m in到校 B.小明刚好按时到校
C.小明可以提前1m in到校 D.小明可以提前2m in到校
变式1.我国古代数学经典著作《九章算术》记载：“今有善行者行一百步，不善行者行六十步.今不善行者先行一百步，善行者追之.问几何步及之 ”如图是善行者与不善行者行走路程s(单位：步)关于善行者的行走时间t的函数图象，则两图象交点P 的纵坐标是 .
变式2.昨天早晨7点，小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他与西安的距离y(千米)与他离家的时间x(小时)之间的函数图象，若昨天下午3点时，小明距西安112千米，则他到家的时间 是 .
专题讲练4 一次函数图象信息(三)——距离与时间
考点一 理解行程问题中距离与路程
【典例1】甲、乙两人在直线跑道上同起点，同终点，同方向匀速跑200米，先到终点的人原地休息，已知甲先跑8米，乙才出发，在跑步过程中，甲、乙两人的距离s(单位：米)与乙出发的时间t(单位：秒)之间的关系如图所示，则图中a 的值是( )
A.44 B.46 C.48 D.50
变式1.甲、乙两车从A 城出发匀速行驶至 B 城，在整个行驶过程中，甲、乙两车离A 城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.则下列结论：①A，B两城相距300 km；②乙车比甲车晚出发1h，却早到1h；③乙车出发2.5 h后追上甲车；④当甲、乙两车相距40 km时, 或 其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
变式2.快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶，图中折线表示快、慢两车之间的距离y(km)与它们的行驶时间x(h)之间的函数关系，小欣同学结合图象得出下列结论：①快车途中停留了0.5h；②快车速度比慢车速度快20km/h;③a=340;④快车先到达目的地.其中正确的是( )
A.①③ B.②③ C.②④ D.①④
考点二 理解图象与坐标轴交点的实际意义
【典例2】甲、乙两人参加200米决赛(环形跑道)，下图表示在比赛中两人之间的距离s(米)与时间t(秒)之间的函数关系(越过终点不计)，根据图中的信息，下列说法不正确的是( )
A.起跑时两人相距15米 B.其中一人的速度为8米/秒
C.一人到达终点时，另一个人距离终点还有25米 D.较慢的人比赛用时为28秒
变式.甲、乙两人沿相同的路线由A 地到B地匀速前进，A、B两地间的路程为20千米，他们前进的路程为s(千米)，甲出发后的时间为t(小时)，甲、乙前进的路程与时间的函数图象如图所示，根据图象信息，下列说法中正确的是( )
A.甲的速度是4千米/小时 B.乙的速度是10千米/小时
C.乙比甲晚出发1小时 D.甲比乙晚3小时到B地
专题讲练1 一次函数图象及性质
【典例1】A 变式1. A 变式2. C 变式3. B
【典例2】B 变式. B
【典例3】1
变式.解：①若两直线无交点，n=1；
②若两直线有交点,交点横坐标x≥2,x+4= nx,
专题讲练2 一次函数图象信息(一)——行程问题(1)
【典例】B 变式1.(4,160) 变式2.350 变式3. C
变式4. B
专题讲练3 一次函数图象信息(二)——行程问题(2)
【典例1】A 变式. D 【典例2】B 变式1.250
变式2.昨天下午4时
专题讲练4 一次函数图象信息(三)——距离与时间
【典例1】C 变式1. C 变式2. B 【典例2】C 变式. C

展开更多......

收起↑