资源简介

中小学教育资源及组卷应用平台
三角函数
专题讲练1 三角函数与实际应用(一)
考点一 利用特殊角及三角函数解直角三角形
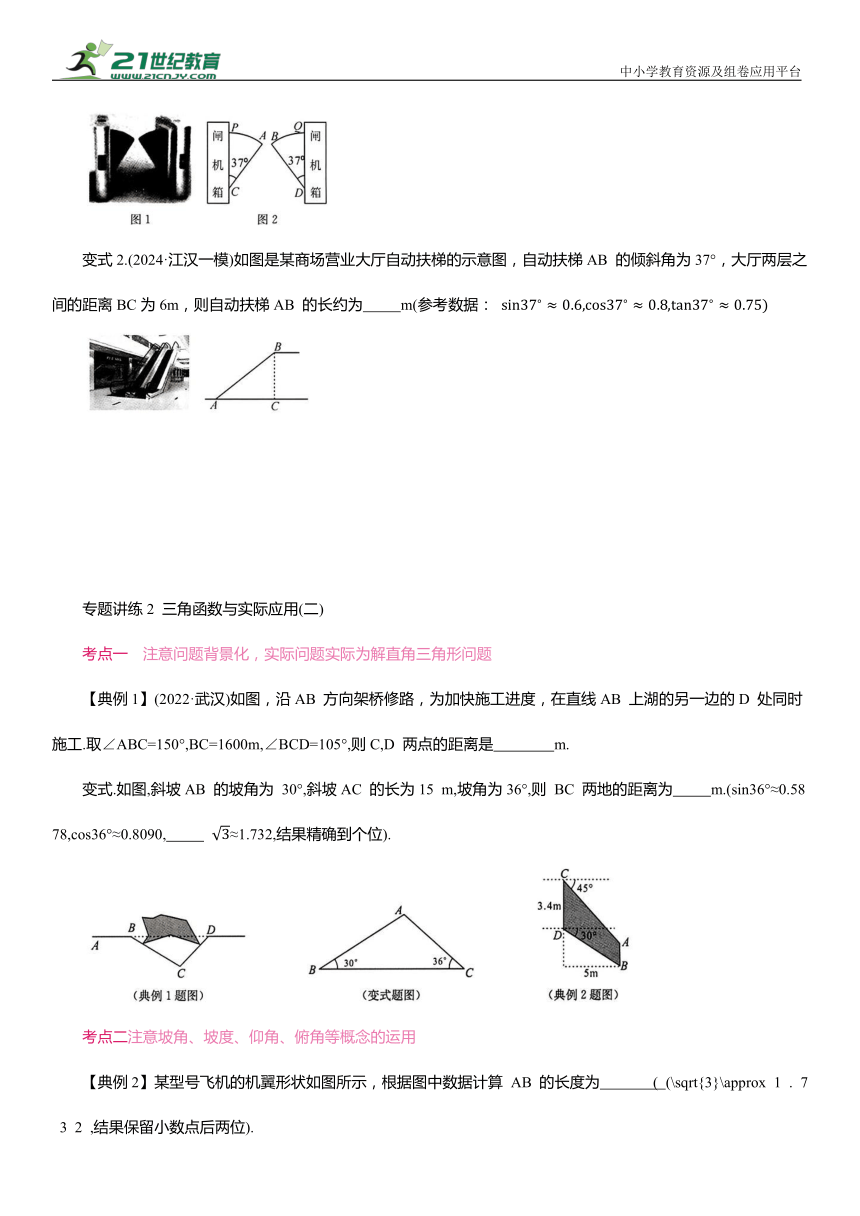
【典例1】(2021·武汉)如图，海中有一个小岛A，一艘轮船由西向东航行，在B 点测得小岛A在北偏东60°方向上，航行12nmile到达C点，这时测得小岛A 在北偏东 30°方向上.小岛 A 到航线BC 的距离是 1 n m i l e(\sqrt{3}\approx 1 . 7 3 ,结果用四舍五入法精确到0.1)
变式.(2021·武汉四调)如图，热气球的探测器显示，从热气球A 看一栋楼顶部B 的仰角为30°，看这栋楼底部C的俯角为60°，热气球A 与楼的水平距离为120m，这栋楼的高度BC 是 m. 结果取整数).
考点二 结合已知三角函数值利用三角函数解直角三角形
【典例2】(2022·武汉四调)如图，一根长为100cm的木棒，斜靠在竖直的墙面上，当木棒与水平地面所成角为50°时，木棒顶端靠在墙面上的点A 处，底端落在水平地面的点 B 处.将木棒底端向外滑动，使木棒与地面所成角为40°，则木棒顶端下降了 cm(结果根据四舍五入法精确到个位，
变式1.如图1是武汉某地铁站入口的双翼闸机.如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC=BD=60cm，且与闸机侧立面夹角∠PCA=∠BDQ=37°,当双翼收起时，可以通过闸机物体的最大宽度为 cm.(参考数据：
变式2.(2024·江汉一模)如图是某商场营业大厅自动扶梯的示意图，自动扶梯AB 的倾斜角为37°，大厅两层之间的距离BC为6m，则自动扶梯AB 的长约为 m(参考数据：
专题讲练2 三角函数与实际应用(二)
考点一 注意问题背景化，实际问题实际为解直角三角形问题
【典例1】(2022·武汉)如图，沿AB 方向架桥修路，为加快施工进度，在直线AB 上湖的另一边的D 处同时施工.取∠ABC=150°,BC=1600m,∠BCD=105°,则C,D 两点的距离是 m.
变式.如图,斜坡AB 的坡角为 30°,斜坡AC 的长为15 m,坡角为36°,则 BC 两地的距离为 m.(sin36°≈0.5878,cos36°≈0.8090, ≈1.732,结果精确到个位).
考点二注意坡角、坡度、仰角、俯角等概念的运用
【典例2】某型号飞机的机翼形状如图所示，根据图中数据计算 AB 的长度为 ( (\sqrt{3}\approx 1 . 7 3 2 ,结果保留小数点后两位).
变式1.大门高ME=7.6米，学生身高BD=1.6米，当学生准备进入体温检测有效识别区域时，在点B 时测得摄像头M的仰角为30°，当学生刚好离开体温检测有效识别区域AB 时，在点A 时测得摄像头M的仰角为60°，则AB 的长是 米.(结果保留根号)
变式2.如图，我市在建高铁的某段路基横断面为梯形ABCD，DC//AB，BC长6米，坡角β为45°，AD 的坡角α为30°,则AD 长为 米(结果保留根号).
变式3.(2024·二中)如图1是一种折叠式晾衣架.晾衣时，该晾衣架水平放置并且右晾衣臂张开后示意图如图2所示,两支脚OC=OD=6分米,展开角∠COD=60°,，晾衣臂OA=8分米，晾衣臂(OA)撑开时与支脚(OC)的夹角∠AOC=105°.则点 A 离地面的距离AM为 分米.(结果保留整数)(参考数据：
专题讲练3 三角函数与实际应用(三)
考点一 将实际问题转化为解三角形
【典例1】(2023·武汉)如图，将45°的∠AOB 按下面的方式放置在一把刻度尺上，顶点O与尺下沿的端点重合，OA 与尺下沿重合，OB 与尺上沿的交点 B 在尺上的读数为2cm，若按相同的方式将37°的∠AOC 放置在该刻度尺上，则OC 与尺上沿的交点C 在尺上的读数是 cm.(结果精确到0.1cm，参考数据
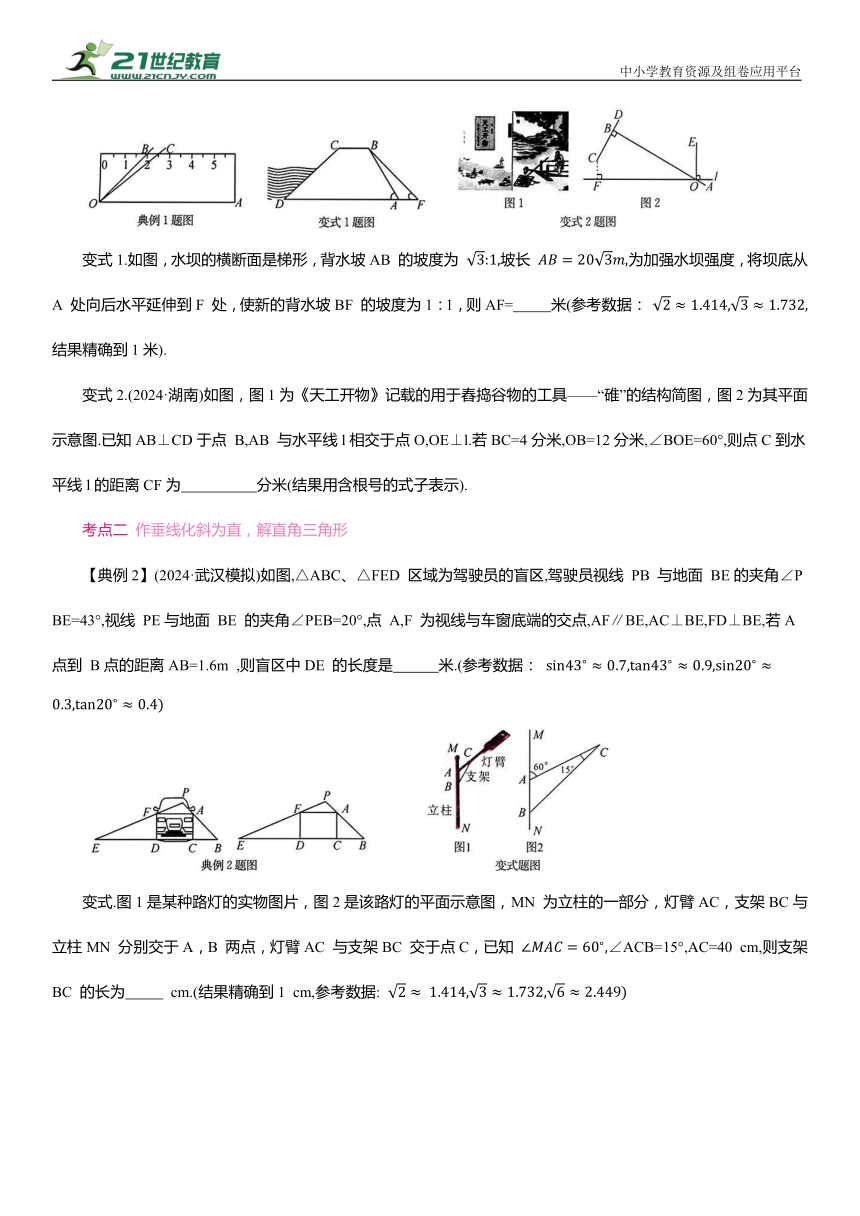
变式1.如图，水坝的横断面是梯形，背水坡AB 的坡度为 坡长 为加强水坝强度，将坝底从A 处向后水平延伸到F 处，使新的背水坡BF 的坡度为1：1，则AF= 米(参考数据： 结果精确到1米).
变式2.(2024·湖南)如图，图1为《天工开物》记载的用于舂捣谷物的工具——“碓”的结构简图，图2为其平面示意图.已知AB⊥CD于点 B,AB 与水平线l相交于点O,OE⊥l.若BC=4分米,OB=12分米,∠BOE=60°,则点C到水平线l的距离CF为 分米(结果用含根号的式子表示).
考点二 作垂线化斜为直，解直角三角形
【典例2】(2024·武汉模拟)如图,△ABC、△FED 区域为驾驶员的盲区,驾驶员视线 PB 与地面 BE的夹角∠PBE=43°,视线 PE与地面 BE 的夹角∠PEB=20°,点 A,F 为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE,若A 点到 B点的距离AB=1.6m ,则盲区中DE 的长度是 米.(参考数据：
变式.图1是某种路灯的实物图片，图2是该路灯的平面示意图，MN 为立柱的一部分，灯臂AC，支架BC与立柱MN 分别交于A，B 两点，灯臂AC 与支架BC 交于点C，已知 ∠ACB=15°,AC=40 cm,则支架BC 的长为 cm.(结果精确到1 cm,参考数据:
专题讲练4 三角函数与几何结合
考点一 结合相似求三角函数
【典例1】(2023·广元)如图,在平面直角坐标系中,已知A(1,0),B(0,-3),点C在x轴上,且在A点右侧， ，则点 C 的坐标为 .
变式.如图,在矩形ABCD中,AB=12,P 是边 AB 上一点,把△PBC 沿直线 PC 折叠,顶点 B 的对应点是点G,过点B作 BE⊥CG,垂足为E 且在AD上,BE 交 PC 于点 F.当AD=25,且AE考点二 注意“A型”相似或三垂相似，双垂相似与三角函数
【典例2】(2023·巴中)如图,已知正方形 ABCD 和正方形 BEFG,点G在AD 上,GF 与CD 交于点 正方形 ABCD 的边长为8,则 BH 的长为 .
变式.(2024·二中)如图,在△ABC 中, 点D,E分别在边 BC,AC上,若. 2CD,连接AD,BE 交于点 F,则 cos∠AFE 值为 .
第四部分 三角函数
专题讲练1 三角函数与实际应用(一)
【典例1】10.4
变式.277
【典例2】12
变式1.82
解:过点A 作AE⊥CP,过点 B 作BF⊥DQ,
Rt△ACE 中,
Rt△BDF 中,
∵双翼边缘的端点A 与B之间的距离为10cm，
当双翼收起时，可以通过闸机的物体的最大宽度为36+36+10=82(cm).
变式2.10
解：由题意可得：
则 解得:AB≈10(m),
答：自动扶梯AB 的长约为10 m.
故答案为：10.
专题讲练2 三角函数与实际应用(二)
【典例
变式.27
【典例2】1.29 m
变式1.4
变式2.6
变式3.11
专题讲练3 三角函数与实际应用(三)
【典例1】2.7
变式1.13
变式
【典例2】2.8
变式.49
专题讲练4 三角函数与几何结合
【典例
解:易知∠ABO=∠ABC,过点A 作AM⊥BC,
∴AO=AM=1,△ACM∽△BCO,AMB=AC=
设AC=m,BC=3m,
或--1(舍),
变式.解:△ABE∽△DEC,AE=9,DE=16,
∴BE=15,CE=20,设PB=x=BF,又△CEF∽△CGP,
【典例2】10
解:△ABG∽△DGH,DG=4,DH=2,
变式.
解:作DM⊥AD,作BM⊥BC 相交于点M,连接AM,△BDM∽△CAD,
∴BM=2CD=AE,

展开更多......

收起↑