资源简介

中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺练习四边形与三角函数综合问题训练
1．如图，在四边形ABCD中，E是AB的中点，DB，CE交于点F，DF＝FB，AF∥DC．
（1）求证：四边形AFCD为平行四边形；
（2）若∠EFB＝90°，tan∠FEB＝3，EF＝1，求BC的长．
2．如图，在 ABCD中，点E，F分别在BC，AD上，BE＝DF，AC＝EF．
（1）求证：四边形AECF是矩形；
（2）若AE＝BE，AB＝2，tan∠ACB，求BC的长．
3．如图，在四边形ABCD中，∠ACB＝∠CAD＝90°，点E在BC上，AE∥DC，EF⊥AB，垂足为F．
（1）求证：四边形AECD是平行四边形；
（2）若AE平分∠BAC，BE＝5，cosB，求BF和AD的长．
4．如图，在 ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．
（1）求证：四边形ABEF是菱形；
（2）若AB＝4，AD＝6，∠ABC＝60°，求tan∠ADP的值．
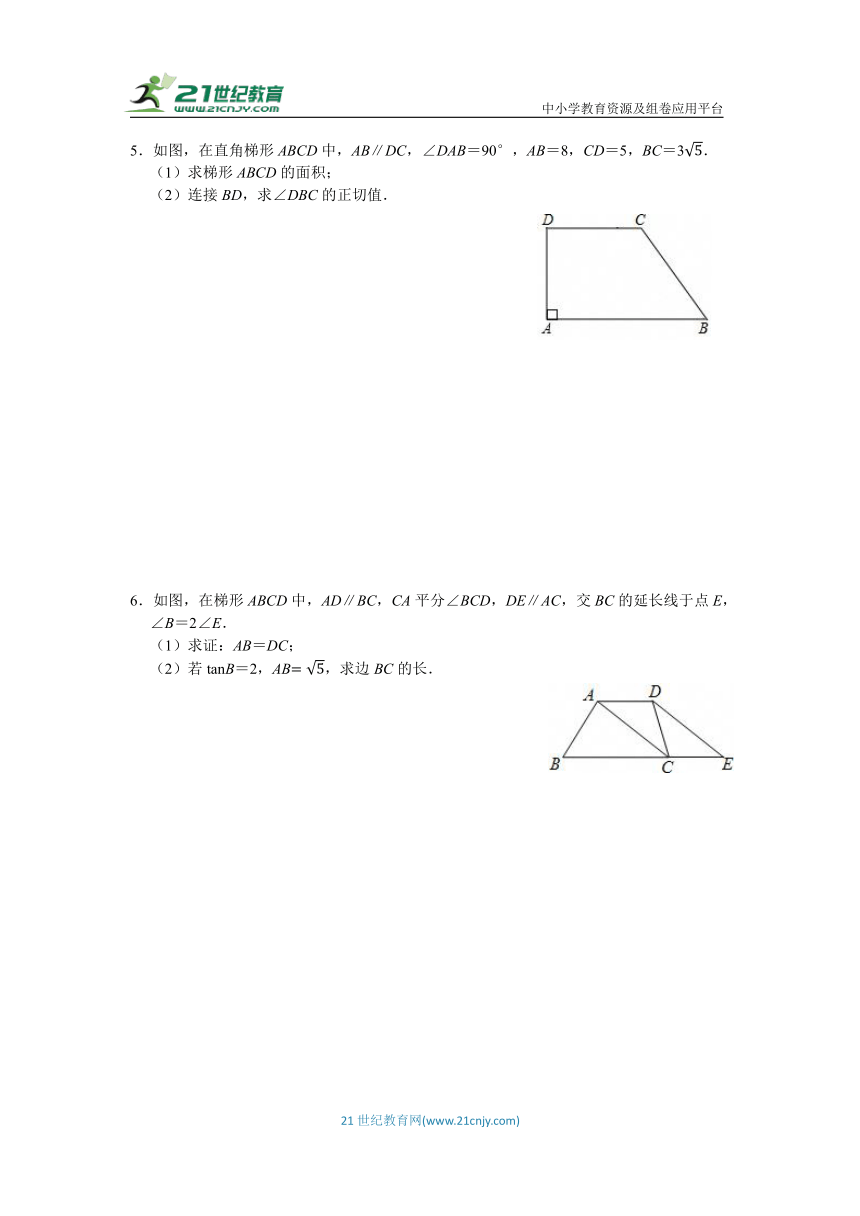
5．如图，在直角梯形ABCD中，AB∥DC，∠DAB＝90°，AB＝8，CD＝5，BC＝3．
（1）求梯形ABCD的面积；
（2）连接BD，求∠DBC的正切值．
6．如图，在梯形ABCD中，AD∥BC，CA平分∠BCD，DE∥AC，交BC的延长线于点E，∠B＝2∠E．
（1）求证：AB＝DC；
（2）若tanB＝2，AB，求边BC的长．
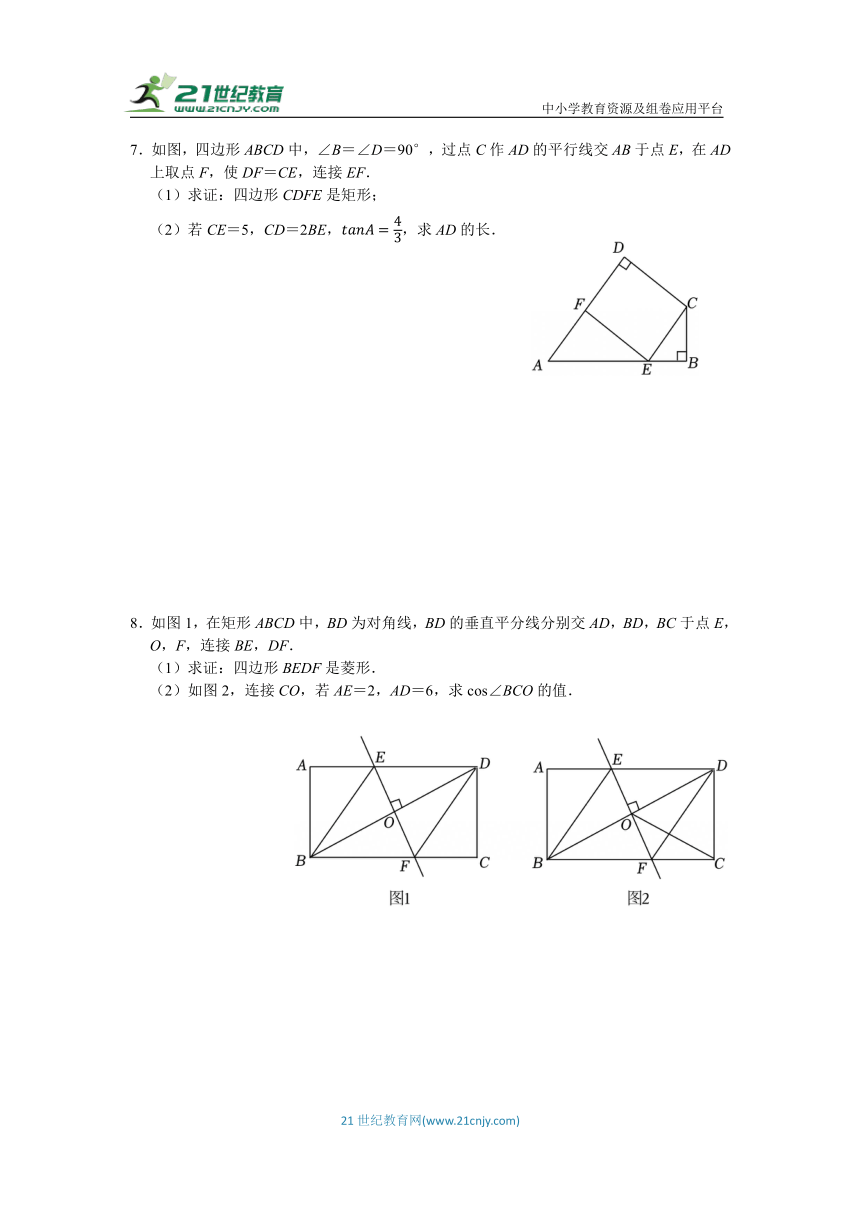
7．如图，四边形ABCD中，∠B＝∠D＝90°，过点C作AD的平行线交AB于点E，在AD上取点F，使DF＝CE，连接EF．
（1）求证：四边形CDFE是矩形；
（2）若CE＝5，CD＝2BE，，求AD的长．
8．如图1，在矩形ABCD中，BD为对角线，BD的垂直平分线分别交AD，BD，BC于点E，O，F，连接BE，DF．
（1）求证：四边形BEDF是菱形．
（2）如图2，连接CO，若AE＝2，AD＝6，求cos∠BCO的值．
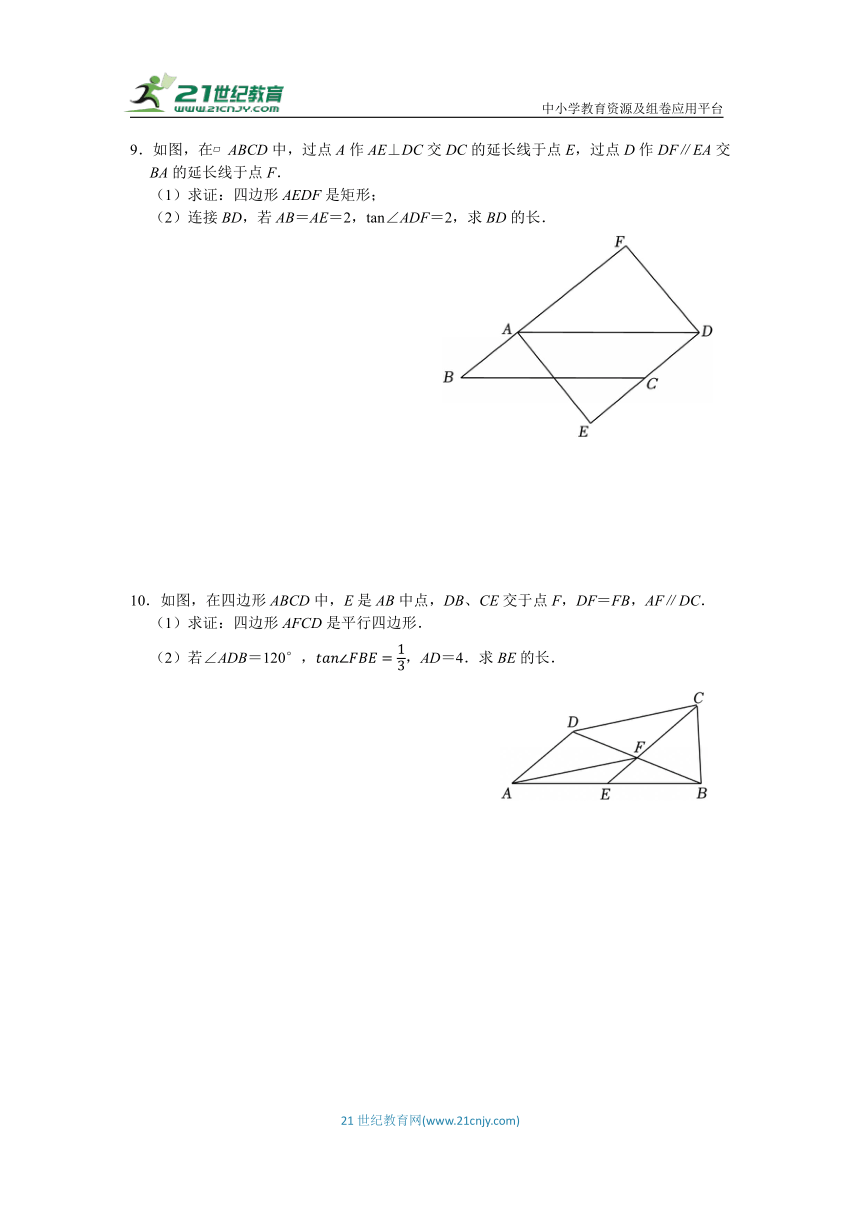
9．如图，在 ABCD中，过点A作AE⊥DC交DC的延长线于点E，过点D作DF∥EA交BA的延长线于点F．
（1）求证：四边形AEDF是矩形；
（2）连接BD，若AB＝AE＝2，tan∠ADF＝2，求BD的长．
10．如图，在四边形ABCD中，E是AB中点，DB、CE交于点F，DF＝FB，AF∥DC．
（1）求证：四边形AFCD是平行四边形．
（2）若∠ADB＝120°，，AD＝4．求BE的长．
11．如图，在 ABCD中，AE⊥BC于点E，点F在BC的延长线上，且CF＝BE，连接DF．
（1）求证：四边形AEFD是矩形；
（2）连接DE，若tan∠ABC＝2，BE＝1，AD＝4，求DE的长．
12．如图，在四边形ABCD中，AB∥CD，AB＝AD，对角线AC，BD交于O，AC平分∠BAD．
（1）求证：四边形ABCD是菱形；
（2）过点C作AB的垂线交其延长线于点E，若BD＝6，，求CE的长．
13．如图，点E在 ABCD的对角线DB的延长线上，AE＝AD，AF⊥BD于点F，EG∥BC交AF的延长线于点G，连接DG．
（1）求证：四边形AEGD是菱形；
（2）若AF＝BF，tan∠AEF，AB＝4，求菱形AEGD的面积．
14．如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，连接CD，过点A作AG∥DC，过点C作CG∥DA，AG与CG相交于点G．
（1）求证：四边形ADCG是菱形；
（2）若AB＝10，tan∠CAG，求BC的长．
15．如图，在 ABCD中，AC，BD交于点O，且AO＝BO．
（1）求证：四边形ABCD是矩形；
（2）∠ADB的角平分线DE交AB于点E，当AD＝6，tan∠CAB时，求AE的长．
参考答案
1．【解答】（1）证明：∵E是AB的中点，
∴AE＝BE，
∵DF＝BF，
∴EF是△ABD的中位线，
∴EF∥AD，
∴CF∥AD，
∵AF∥CD，
∴四边形AFCD为平行四边形；
（2）解：由（1）知，EF是△ABD的中位线，
∴AD＝2EF＝2，
∵∠EFB＝90°，tan∠FEB＝3，
∴BF＝3EF＝3，
∵DF＝FB，
∴DF＝BF＝3，
∵AD∥CE，
∴∠ADF＝∠EFB＝90°，
∴AF，
∵四边形AFCD为平行四边形，
∴CD＝AF，
∵DF＝BF，CE⊥BD，
∴BC＝CD．
2．【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∵BE＝DF，
∴AD﹣DF＝BC﹣BE，
即AF＝EC，
∴四边形AECF是平行四边形，
∵AC＝EF，
∴平行四边形AECF是矩形；
（2）解：∵四边形AECF是矩形，
∴∠AEC＝∠AEB＝90°，
∵AE＝BE，AB＝2，
∴△ABE是等腰直角三角形，
∴AE＝BEAB，
∵tan∠ACB，
∴EC＝2AE＝2，
∴BC＝BE+EC23，
即BC的长为3．
3．【解答】（1）证明：∵∠ACB＝∠CAD＝90°，
∴AD∥CE，
∵AE∥DC，
∴四边形AECD是平行四边形；
（2）解：∵EF⊥AB，
∴∠BFE＝90°，
∵cosB，BE＝5，
∴BFBE5＝4，
∴EF3，
∵AE平分∠BAC，EF⊥AB，∠ACE＝90°，
∴EC＝EF＝3，
由（1）得：四边形AECD是平行四边形，
∴AD＝EC＝3．
4．【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC．
∴∠DAE＝∠AEB．
∵AE是角平分线，
∴∠DAE＝∠BAE．
∴∠BAE＝∠AEB．
∴AB＝BE．
同理AB＝AF．
∴AF＝BE．
∴四边形ABEF是平行四边形．
∵AB＝BE，
∴四边形ABEF是菱形．
（2）解：作PH⊥AD于H，
∵四边形ABEF是菱形，∠ABC＝60°，AB＝4，
∴AB＝AF＝4，∠ABF＝∠AFB＝30°，AP⊥BF，
∴APAB＝2，
∴PH，AH＝1，
∴DH＝5，
∴tan∠ADP．
5．【解答】解：（1）过C作CE⊥AB于E，
∵AB∥DC，∠DAB＝90°，
∴∠ADC＝90°，
∴∠A＝∠ADC＝∠AEC＝90°，
∴四边形ADCE是矩形，
∴AD＝CE，AE＝CD＝5，
∴BE＝AB﹣AE＝3，
∵BC＝3，
∴CE6，
∴梯形ABCD的面积（5+8）×6＝39；
（2）过C作CH⊥BD于H，
∵CD∥AB，
∴∠CDB＝∠ABD，
∵∠CHD＝∠A＝90°，
∴△CDH∽△DBA，
∴，
∵BD10，
∴，
∴CH＝3，
∴BH6，
∴∠DBC的正切值．
6．【解答】（1）证明：∵DE∥AC，
∴∠BCA＝∠E．（1分）
∵CA平分∠BCD，
∴∠BCD＝2∠BCA，（1分）
∴∠BCD＝2∠E，（1分）
又∵∠B＝2∠E，
∴∠B＝∠BCD．（1分）
∴梯形ABCD是等腰梯形，即AB＝DC．（2分）
（2）解：如图，作AF⊥BC，DG⊥BC，垂足分别为F，G，则AF∥DG．
在Rt△AFB中，tanB＝2，∴AF＝2BF．（1分）
又∵AB，且AB2＝AF2+BF2，
∴5＝4BF2+BF2，得BF＝1．（1分）
同理可知，在Rt△DGC中，CG＝1．（1分）
∵AD∥BC，∴∠DAC＝∠ACB．
又∵∠ACB＝∠ACD，∴∠DAC＝∠ACD，∴AD＝DC．∵DC＝AB，∴AD．（1分）
∵AD∥BC，AF∥DG，∴四边形AFGD是平行四边形，∴FG＝AD．（1分）
∴BC＝BF+FG+GC＝2．（1分）
7．【解答】（1）证明：∵CE∥AD，DF＝CE，
∴四边形CDFE是平行四边形，
∵∠D＝90°，
∴平行四边形CDFE是矩形；
（2）解：∵CE∥AD，
∴∠CEB＝∠A，
∵tanA＝4/3，
∴tan∠CEB＝tanA，
∵∠B＝90°，
∴△CBE是直角三角形，
在Rt△CBE中，tan∠CEB，
∴设BC＝4a，BE＝3a，
由勾股定理得：CE5a，
∵CE＝5，
∴5a＝5，
解得：a＝1，
∴BE＝3a＝3，
∴CD＝2BE＝6，
由（1）可知：四边形CDFE是矩形，
∴DF＝CE＝5，EF＝CD＝6，∠EFD＝90°，
∴△AEF是直角三角形，
在Rt△AEF中，tanA，
∴，
∴AF＝4.5，
∴AD＝AF+DF＝4.5+5＝9.5．
8．【解答】（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，AB＝CD，
∴∠EDO＝∠FBO，DE∥BF，
∵EF是BD的垂直平分线，
∴OB＝OD，BE＝DE，
∴∠BDF＝∠DBF，
在△DOE和△BOF中，
，
∴△DOE≌△BOF（ASA），
∴DE＝BF，
∴四边形BEDF是平行四边形，
∵EF⊥BD，
∴四边形BEDF是菱形；
（2）解：∵四边形ABCD是矩形，
∴∠A＝90°，
∵EF是BD的垂直平分线，
∴BE＝DE＝AD﹣AE＝6﹣2＝4，
∴AB2，
∴BD4
∵OB＝OD，∠BCD＝90°，
∴OB＝OC，
∴∠BCO＝∠CBD＝∠ADB，
∴cos∠BCO＝cos∠ADB．
9．【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥DC，
∵DF∥EA，
∴四边形AEDF是平行四边形，
∵AE⊥DE，
∴∠E＝90°，
∴四边形AEDF是矩形；
（2）解：如图，
∵四边形AEDF是矩形，
∴AE＝DF＝2，∠F＝90°，
∴，
∴AF＝2DF＝4，
∴BF＝AB+AF＝6，
∴在Rt△BDF中，
．
10．【解答】（1）证明：∵DB、CE交于点F，DF＝FB，
∴F是DB的中点，
∵E是AB的中点，
∴EF∥AD，
∴CF∥AD，
∵AF∥DC，
∴四边形AFCD是平行四边形．
（2）解：作AH⊥BD交BD的延长线于点H，则∠H＝90°，
∵∠ADB＝120°，AD＝4，
∴∠ADH＝90°﹣∠ADB＝60°，
∴sin60°，
∴AHAD4＝2，
∵tan∠FBE，
∴BH＝3AH＝3×26，
∴AB2，
∴BEAB2，
∴BE的长是．
11．【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵CF＝BE，
∴CF+EC＝BE+EC，即BC＝EF，
∴AD＝EF且AD∥EF，
∴四边形AEFD是平行四边形，
∵AE⊥BC，
∴∠AEF＝90°，
∴四边形AEFD是矩形．
（2）解：连接DE，
在Rt△ABE中，∠AEB＝90°，BE＝1，
∵，
∴AE＝2BE＝2，
在Rt△ADE中，∠DAE＝90°，AD＝4，
∴．
12．【解答】（1）证明：∵AB∥CD，
∴∠CAB＝∠DCA，
∵AC为∠DAB的平分线，
∴∠CAB＝∠DAC，
∴∠DCA＝∠DAC，
∴AD＝CD，
∵AB＝AD，
∴AB＝CD，
∵AB∥CD，
∴四边形ABCD是平行四边形，
又∵AB＝AD，
∴平行四边形ABCD是菱形；
（2）解：∵四边形ABCD是菱形，BD＝6，
∴OA＝OC，OB＝ODBD＝3，BD⊥AC，
∴∠AOB＝90°，
∴tan∠OAB，
∴OAOB3＝4，
∴AC＝2OA＝8，AB5，
∵CE⊥AB，
∴S菱形ABCD＝AB CEAC BD8×6＝24，
即5CE＝24，
∴CE，
即CE的长为．
13．【解答】（1）证明：∵AE＝AD，AF⊥BD，
∴EF＝DF，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∵EG∥BC，
∴AD∥EG，
∴∠GEF＝∠ADF，
在△GEF和△ADF中，
，
∴△GEF≌△ADF（ASA），
∴GF＝AF，
∵EF＝DF，
∴四边形AEGD是平行四边形，
∵AE＝AD，
∴四边形AEGD是菱形；
（2）解：∵AF⊥BD，AF＝BF，
∴△AFB是等腰直角三角形，
∵AB＝4，
∴由勾股定理得，，
∵tan∠AEF，
∴，
即，
∴EF，
∵四边形AEGD是菱形，
∴AG＝2AF，ED＝2EF，
∴菱形AEGD的面积．
14．【解答】（1）证明：∵AG∥DC，CG∥DA，
∴四边形ADCG是平行四边形，
∵在Rt△ABC中，∠ACB＝90°，D为AB边的中点，
∴AD＝CDAB，
∴四边形ADCG是菱形；
（2）解：∵CG∥DA，
∴∠BAC＝∠ACG，
∴tan∠CAG＝tan∠BAC，
∴设BC＝3x，AC＝4x，
∴AB＝5x＝10，
∴x＝2，
∴BC＝3x＝6．
15．【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AC＝2AO，BD＝2BO，
∵AO＝BO，
∴AC＝BD，
∴ ABCD为矩形；
（2）解：过点E作EG⊥BD于点G，如图所示：
∵四边形ABCD是矩形，
∴∠DAB＝90°，
∴EA⊥AD，
∵DE为∠ADB的角平分线，
∴EG＝EA，
∵AO＝BO，
∴∠CAB＝∠ABD，
∵AD＝6，tan∠CAB，
∴tan∠CAB＝tan∠ABD，
∴ABAD＝8，
∴BD10，sin∠CAB＝sin∠ABD，
设AE＝EG＝x，则BE＝8﹣x，
在△BEG中，∠BGE＝90°，
∴sin∠ABD，
∴，
解得：x＝3，
∴AE＝3．
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑