资源简介

第20讲 特殊平行四边形的性质与判定
典例精练
【例1】 (2023随州)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若BC=3,DC=2,求四边形OCED的面积.
【例2】 如图，点A，F，C，D在同一条直线上，点 B，E分别在直线AD 的两侧，且. DE,∠A=∠D,AF=DC.
(1)求证：四边形 BCEF 是平行四边形；
(2)若∠ABC=90°,AB=4,BC=3,当AF= 时,四边形 BCEF 是菱形.
【例3】 (2024 贵州)如图,四边形 ABCD的对角线AC 与BD 相交于点O, 有下列条件:①AB∥CD,②AD=BC.
(1)请从以上①②中任选1个作为条件，求证：四边形ABCD 是矩形；
(2)在(1)的条件下,若. ，求四边形ABCD的面积.
针对训练
1.(2024武汉)小美同学按如下步骤作四边形ABCD：①画∠MAN；②以点A为圆心，1个单位长度为半径画弧，分别交AM，AN于点B，D；③分别以点B，D为圆心，1个单位长度为半径画弧,两弧交于点C;④连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
2.(2024成都)如图，在矩形ABCD中，对角线AC与BD 相交于点O，则下列结论一定正确的是( )
A. AB=AD B. AC⊥BD C. AC=BD D.∠ACB=∠ACD
3.(2024吉林)如图,在平面直角坐标系中,点A 的坐标为(-4,0),点C的坐标为(0,2).以OA,OC为边作矩形OABC,若将矩形OABC绕点O顺时针旋转90°,得到矩形OA'B'C',则点 B'的坐标为( )
A.(-4,-2) B.(-4,2) C.(2,4) D.(4,2)
4.(2024四川)如图,在矩形ABCD中,AB=6,BC=8,点E在DC上,把△ADE沿AE 折叠,点 D恰好落在边 BC 上的点 F 处,则 cos∠CEF 的值为( )
C. D.
5.(2024上海)已知四边形ABCD为矩形,过A,C作对角线BD 的垂线,过B,D作对角线AC的垂线，如果以四条垂线为边拼成一个四边形，那这个四边形为( )
A.菱形 B.矩形 C.直角梯形 D.等腰梯形
6.(2024广西)如图，两张宽度均为3cm的纸条交叉叠放在一起，交叉形成的锐角为60°，则重合部分构成的四边形ABCD 的周长为 cm.
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
A.2.5 B.2.4 C.2.2 D.2
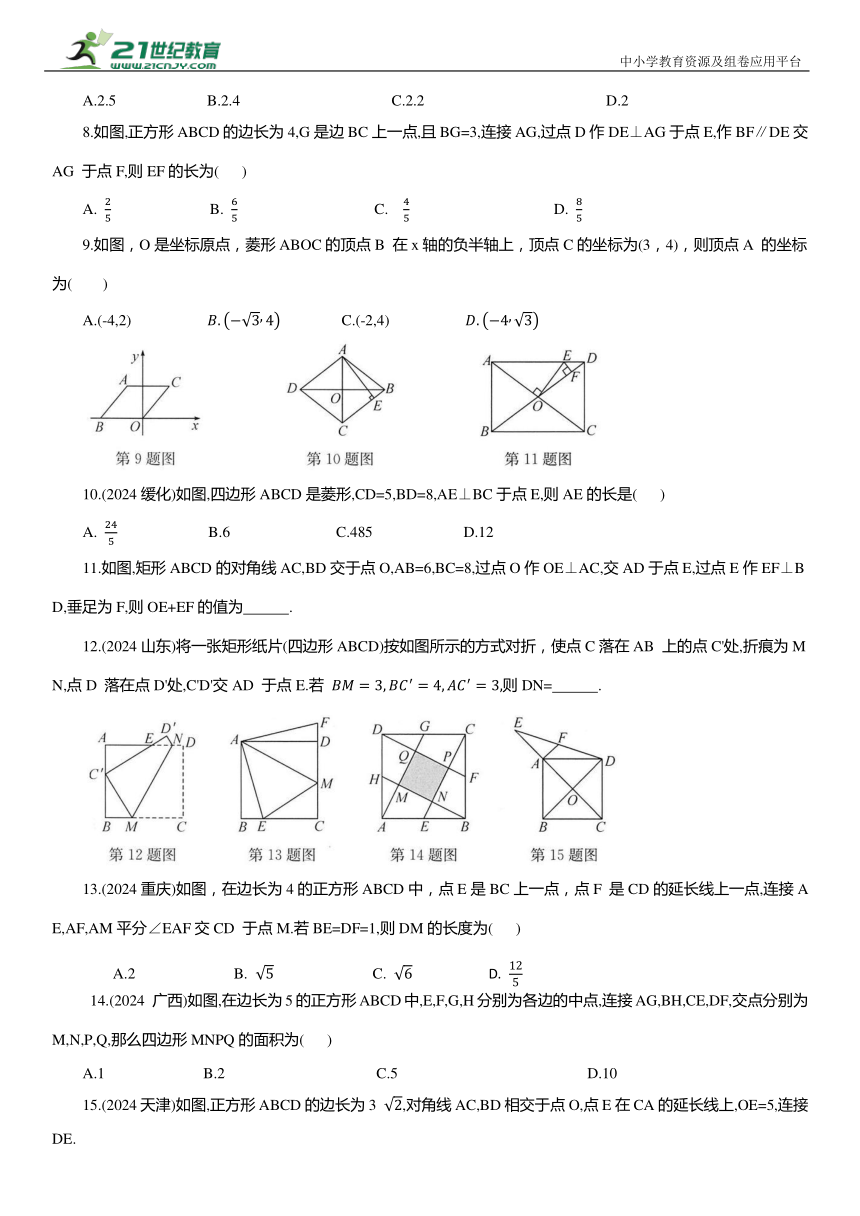
8.如图,正方形ABCD的边长为4,G是边BC上一点,且BG=3,连接AG,过点D作DE⊥AG于点E,作BF∥DE交AG 于点F,则EF的长为( )
A. B. C. D.
9.如图，O是坐标原点，菱形ABOC的顶点B 在x轴的负半轴上，顶点C的坐标为(3，4)，则顶点A 的坐标为( )
A.(-4,2) C.(-2,4)
10.(2024缓化)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C.485 D.12
11.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为 .
12.(2024山东)将一张矩形纸片(四边形ABCD)按如图所示的方式对折，使点C落在AB 上的点C'处,折痕为MN,点D 落在点D'处,C'D'交AD 于点E.若 则DN= .
13.(2024重庆)如图，在边长为4的正方形ABCD中，点E是BC上一点，点F 是CD的延长线上一点,连接AE,AF,AM平分∠EAF交CD 于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
14.(2024 广西)如图,在边长为5的正方形ABCD中,E,F,G,H分别为各边的中点,连接AG,BH,CE,DF,交点分别为M,N,P,Q,那么四边形MNPQ的面积为( )
A.1 B.2 C.5 D.10
15.(2024天津)如图,正方形ABCD的边长为3 ,对角线AC,BD相交于点O,点E在CA的延长线上,OE=5,连接DE.
(1)线段AE的长为 ;
(2)若 F 为DE 的中点,则线段 AF 的长为 .
16.(2024包头)如图,在菱形ABCD中, ，AC是一条对角线，E是AC 上一点，过点E作 垂足为F，连接DE.若 求DE的长.
17.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD 的中点,连接OE.过点C作 交OE 的延长线于点F，连接DF.求证：
(2)四边形OCFD 是矩形.
18.(2024呼伦贝尔)如图,在平行四边形ABCD中,点F在边AD 上, 连接 BF,点O为BF 的中点，AO的延长线交边BC 于点E，连接EF.
(1)求证:四边形ABEF 是菱形;
(2)若平行四边形ABCD的周长为22， 求AE的长.
19.如图,矩形 EFGH 的顶点E,G分别在菱形ABCD 的边AD,BC上,顶点 F,H 在菱形ABCD的对角线BD 上.
(1)求证:
(2)若E为AD的中点, ，求菱形ABCD的周长.
第20 讲 特殊平行四边形的性质与判定
典例精练
【例1】 (2023随州)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若BC=3,DC=2,求四边形OCED的面积.
解:(1)证明:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形.
又∵在矩形ABCD中,OC=OD,∴□OCED是菱形.
(2)由题意,得S矩形ABCD=BC·CD=6.
【例2】 如图,点A,F,C,D在同一条直线上,点 B,E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(1)求证：四边形 BCEF 是平行四边形；
(2)若∠ABC=90°,AB=4,BC=3,当 时,四边形 BCEF 是菱形.
解:(1)证明:∵AF=DC,∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
∴BC=EF,∠ACB=∠DFE.∴BC∥EF.
∴四边形 BCEF 是平行四边形.
【例3】 (2024 贵州)如图,四边形 ABCD 的对角线AC 与BD 相交于点O,AD∥BC,∠ABC=90°,有下列条件:①AB∥CD,②AD=BC.
(1)请从以上①②中任选1个作为条件，求证：四边形ABCD 是矩形；
(2)在(1)的条件下,若AB=3,AC=5,求四边形ABCD的面积.
解:(1)选择①.
证明:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.
又∵∠ABC=90°,∴四边形ABCD是矩形.
选择②.
证明:∵AD=BC,AD∥BC,∴四边形ABCD是平行四边形.
又∵∠ABC=90°,∴四边形ABCD是矩形.
∴矩形ABCD的面积是3×4=12.
针对训练
1.(2024武汉)小美同学按如下步骤作四边形ABCD：①画∠MAN；②以点A为圆心，1个单位长度为半径画弧，分别交AM，AN于点B，D；③分别以点 B，D为圆心，1个单位长度为半径画弧,两弧交于点C;④连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( C)
A.64° B.66° C.68° D.70°
2.(2024成都)如图，在矩形ABCD中，对角线AC与BD 相交于点O，则下列结论一定正确的是(C)
A. AB=AD B. AC⊥BD C. AC=BD D.∠ACB=∠ACD
3.(2024吉林)如图,在平面直角坐标系中,点A 的坐标为(-4,0),点C的坐标为(0,2).以OA,OC为边作矩形OABC,若将矩形OABC绕点O顺时针旋转90°,得到矩形OA'B'C',则点 B'的坐标为(C)
A.(-4,-2) B.(-4,2) C.(2,4) D.(4,2)
4.(2024四川)如图,在矩形ABCD中,AB=6,BC=8,点E在DC上,把△ADE沿AE 折叠,点D恰好落在边BC上的点 F 处,则cos∠CEF 的值为(A)
C. D.
5.(2024上海)已知四边形ABCD为矩形,过A,C作对角线BD 的垂线,过B,D作对角线AC的垂线，如果以四条垂线为边拼成一个四边形，那这个四边形为(A)
A.菱形 B.矩形 C.直角梯形 D.等腰梯形
6.(2024广西)如图，两张宽度均为3cm的纸条交叉叠放在一起，交叉形成的锐角为60°，则重合部分构成的四边形ABCD 的周长为 8 cm.
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB 上一动点,过点 D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是(B)
A.2.5 B.2.4 C.2.2 D.2
8.如图,正方形ABCD的边长为4,G是边BC上一点,且BG=3,连接AG,过点D作DE⊥AG于点E,作BF∥DE交AG于点F,则EF的长为(C)
A. B. C. D.
9.如图，O是坐标原点，菱形ABOC的顶点B 在x轴的负半轴上，顶点C的坐标为(3，4)，则顶点A的坐标为(C)
A.(-4,2) C.(-2,4)
10.(2024缓化)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是(A)
A.
11.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为
12.(2024山东)将一张矩形纸片(四边形ABCD)按如图所示的方式对折，使点C落在AB 上的点C'处,折痕为MN,点D 落在点D'处,C'D'交AD 于点E.若 则
13.(2024重庆)如图,在边长为4的正方形ABCD中,点E是BC上一点,点F 是CD 的延长线上一点,连接AE,AF,AM平分∠EAF交CD 于点M.若BE=DF=1,则 DM的长度为(D)
A.2 B. C. D.
14.(2024 广西)如图,在边长为5的正方形ABCD中,E,F,G,H分别为各边的中点,连接AG,BH,CE,DF,交点分别为M,N,P,Q,那么四边形MNPQ的面积为(C)
A.1 B.2 C.5 D.10
15.(2024天津)如图,正方形ABCD的边长为 ,对角线AC,BD 相交于点O,点E在CA 的延长线上,OE=5,连接DE.
(1)线段AE 的长为 2 ;
中小学教育资源及组卷应用平台
(2)若F 为DE 的中点,则线段AF的长.
16.(2024 包头)如图,在菱形ABCD中, ，AC是一条对角线，E是AC 上一点,过点 E作EF⊥AB,垂足为F,连接DE.若 求 DE的长.
解:过D作DH⊥AC于H.
∵在菱形ABCD中,∠ABC=60°,AB=6,
∴AB=BC=CD=AD,∠ADC=∠ABC=60°.
∴△ABC,△ACD都是等边三角形.
∵EF⊥AB,∴∠AEF=30°,∴AE=2AF.
又∵CE=AF,∴AE=2CE,
∴CE=2,∴HE=CH-CE=1.
在 Rt△CDH中,
17.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD 的中点,连接OE.过点 C作CF∥BD交OE 的延长线于点F,连接DF.求证:
(1)△ODE≌△FCE;
(2)四边形OCFD是矩形.
证明:(1)∵E是CD 的中点,∴DE=CE.
∵CF∥OD,∴∠ODE=∠FCE.
在△ODE 和△FCE中
(2)∵△ODE≌△FCE,∴OD=CF.
∵CF∥BD,∴四边形OCFD是平行四边形.
∵四边形 ABCD 是菱形,∴AC⊥BD.∴∠COD=90°.
∴四边形OCFD 是矩形.
18.(2024呼伦贝尔)如图,在平行四边形ABCD中,点F在边AD 上, 连接BF,点O为BF的中点，AO的延长线交边BC于点E，连接EF.
(1)求证:四边形ABEF 是菱形;
(2)若平行四边形ABCD的周长为22,( 求AE的长.
解：(1)证明：∵四边形ABCD是平行四边形，
∴AD∥BC,即AF∥BC.
∴∠AFB=∠EBF,∠FAE=∠BEA.
∵O为BF的中点,∴BO=FO.
∴△AOF≌△EOB.∴BE=FA.
∵AF∥BE,∴四边形ABEF是平行四边形.
又AB=BF,∴四边形ABEF 是菱形.
(2)∵AD=BC,AF=BE,∴DF=CE=1.
∵平行四边形ABCD的周长为22，
∴菱形ABEF的周长为22-2=20.
∴AB=20÷4=5.∵四边形ABEF是菱形,
又AB=BE,∴△ABE是等边三角形.
∴AE=AB=5.
19.如图,矩形 EFGH 的顶点E,G分别在菱形ABCD 的边AD,BC上,顶点 F,H 在菱形ABCD的对角线BD 上.
(1)求证:BG=DE;
(2)若E为AD的中点,FH=2,求菱形ABCD的周长.
解:(1)证明:∵在矩形EFGH中,EH=FG,EH∥FG,∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,∴∠BFG=∠DHE.
在菱形ABCD中,AD∥BC,∴∠GBF=∠EDH.
∴△BGF≌△DEH(AAS).∴BG=DE.
(2)连接EG.在菱形ABCD中,AD∥BC,AD=BC.
∵E为AD 的中点,∴AE=DE.由(1)知BG=DE,∴AE=BG.
∴四边形ABGE 为平行四边形.∴AB=EG.
在矩形 EFGH中,EG=FH=2.∴AB=2.
∴菱形 ABCD的周长为8.

展开更多......

收起↑