资源简介

九年级三月份限时作业训练数学参考答案及评分细则
（※若有其他正确解法或证法，请参照此标准赋分）
一、选择题（本题包括 10 小题，每小题 3分，共 30分）
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C C C D B A B D
二、填空题（本题包括 5小题，每小题 3分，共 15 分）
11. x1 = 0, 2 = 2 12. √7 13.2√5 2 14. 2 15. 40
三、解答题（本题包括 8小题，共 75分）
16.（10分）
（1）原式= √2 . ………………………………5分
（2）原式=2 . ………………………………10分
17.（8分）
（1）解：设甲种读本每本 x元，乙种读本每本 y元.
25 + 45 = 650
根据题意，得{ , ………………………………3分
40 + 30 = 620
= 8
解这个方程组，得{ .
= 10
答：甲种读本每本 8 元，乙种读本每本 10元. ………………………………5分
（2）解：设学校购买乙种读本 m本，则购买甲种读本 3m本.
根据题意，得8 × 3m + 10m ≤ 680 , ………………………………6分
解这个不等式，得m ≤ 20 .
答：学校最多能购买乙种读本 20本. ………………………………8分
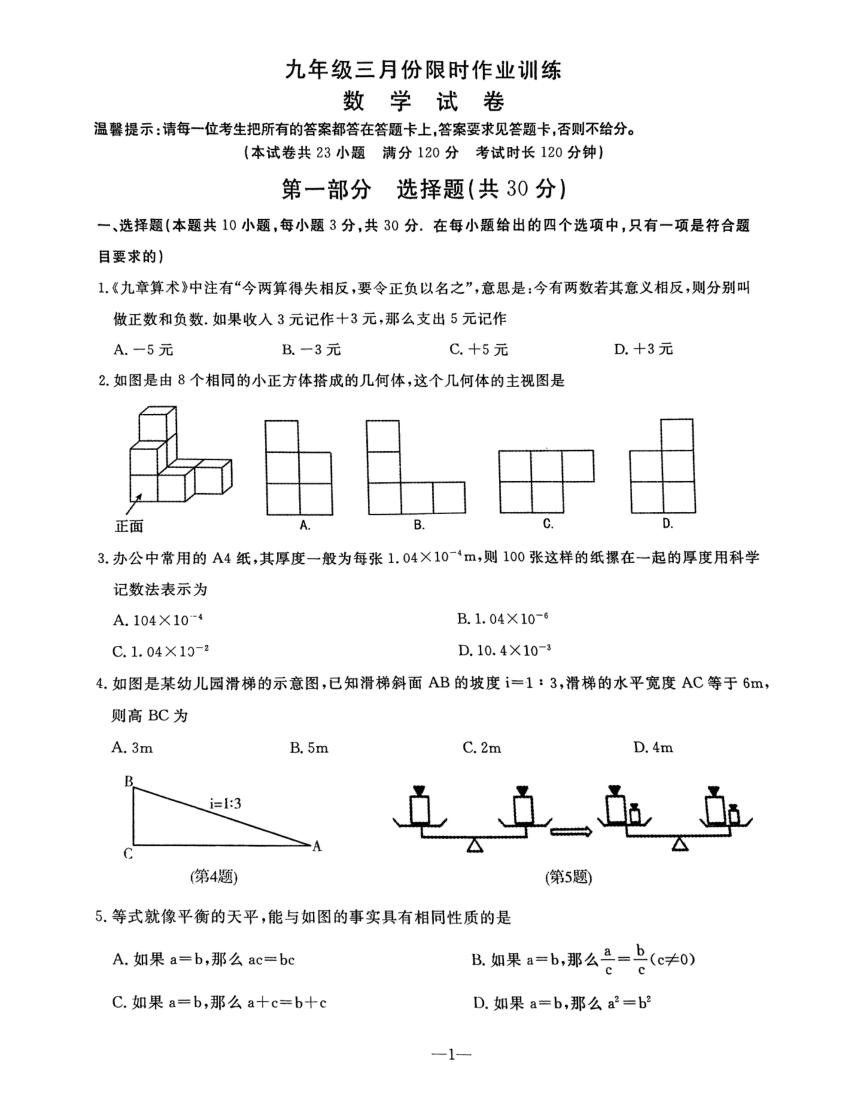
18.（8分）
解：（1） 50 ， ………………………………1分
20 ÷ 40% = 50（名），50 × 20% = 10（名）.
补全条形图（略）. ………………………………3分
（2） 108 . ………………………………5分
20+15+10
（3）600 × = 540（名）.
50
答：估计该校学生在寒假期间一周帮助父母做家务的时间不少于 3 小时的人数大约为
540人． ………………………………8分
19.（8分）
解：（1）y = 120 10(x 48) = 10x + 600. ………………………………3分
（2）w = (x 40)y = (x 40)( 10x + 600) = 10 2 + 1000 24000
= 10( 50)2 + 1000. ………………………………6 分
∵a = 10 < 0,且 x ≥ 48，
∴当 x=50时，w有最大值，w 最大=1000. ………………………………7 分
答：当每箱售价定为 50元时，每天销售的利润最大，最大利润是 1000 元.
………………………………8 分
20.（8分）
解：（1）如答图，过点 D作 DE⊥AB，垂足为 E.
由题意知，AB=7km, ∠DAE=45 ，∠BDE=37 ，∠C=63 ，∠CAB=90 .
∵∠ADE=90 -∠DAE=45 =∠DAE, C
∴DE=AE. ………………………………1 分
B
在 Rt△BDE中， = tan∠BDE = tan37 , A E

7
∴ = ≈ 0.75, 解得 AE=4. ……………………2 分
D
答图
∴AD = √ 2 + 2 = √2 = 4√2 ≈ 5.6(km).
答：AD的长度约为 5.6km. ………………………………3 分
（2）在 Rt△BDE中，
BD = √ 2 + 2 = √(7 4)2 + 42 = 5,
∴线路 2的路线长为 AD+BD=5.6+5=10.6(km). ………………………………4 分
在 Rt△ABC中，
7 7 7 7
AC = = ≈ = 3.5, BC = = ≈ ≈ 7.9,
∠ 63° 2 ∠ 63° 0.89
∴线路 1的路线长为 AC+BC=3.5+7.9=11.4(km). ………………………………7 分
∵10.6km<11.4km,
∴线路 2更短. ………………………………8 分
21.（8分）
（1）证明：如答图，连接 OD.
∵EF⊥AC,
A
∴∠AEF=90 . ………………………………1 分
∵AB=AC,
G O
∴∠C=∠ABC. E
C B
∵OD=OB, D
∴∠ODB=∠OBD. F答图
∴∠C=∠ODB,
∴OD∥AC, ………………………………2 分
∴∠ODF=∠AEF=90 ,即 OD⊥EF. ………………………………3 分
∵OD为⊙O的半径，
∴EF与⊙O相切. ………………………………4 分
（2）∵DB=BF,
∴∠BDF=∠F.
∵∠ODF=90 ,
∴∠BDO+∠BDF=90 , ∠BOD+∠F=90 ,
∴∠BDO=∠BOD,
∴BO=BD=5.
∵OD=OB=BD,
∴∠BOD=∠BDO=∠OBD=60 . ………………………………5 分
60 ×52 25
∴ 扇形 = = . ………………………………6 分 360 6
∵DF = √ 2 2 = √(5 + 5)2 52 = 5√3,
1 1 25√3
∴ △ODF = = × 5 × 5√3 = . ………………………………7 分 2 2 2
25√3 25
∴S阴影 = △ODF 扇形 = . ………………………………8 分 2 6
22.（12分）
（1） 正方形 . ………………………………1 分
（2）AE=EM. ………………………………2 分
证明：如答图 1，连接 EG.
∵四边形 ABCD是矩形，
∴∠ABC=∠C=90 , AB∥CD.
D E C
由折叠，得△BFE≌△BCE,
G
∴∠BFE=∠C=90 , ∠FBE=∠CBE=45 , FE=CE.
∵∠AFE=180 -∠BFE=90 =∠C, AF=CG, FE=CE, M
∴△AFE≌△GCE. ………………………………3 分 A BF
∴∠AEF=∠GEC, EA=EG. 答图 1
∵∠AEG=∠AEF+∠FEG=∠GEC+∠FEG=∠CEF=∠AFE=90 ,
∴∠EAG=∠EGA=45 . ………………………………4 分
∵AM平分∠BAG,
∴∠BAM=∠GAM.
又∠EAM=∠EAG+∠GAM, ∠EMA=∠EBA+∠BAM,
∠EAG=∠EBA=45 ,
∴∠EAM=∠EMA,
∴AE=EM. ………………………………5 分
（3）①证明：如答图 2,过点 M作 MH⊥AB于点 H,作 MP⊥EF于点 P,过点 E作 EQ⊥AG于点 Q.
∵∠MHF=∠HFP=∠MPF=90 , D E C
∴四边形 MHFP是矩形，
G
∴PF=MH, PM∥FH, N
Q
∴∠PME=∠ABE=∠QAE=45 . P M
又∠MPE=∠AQE=90 , ME=AE, A BF H
∴△MPE≌△AQE, 答图 2
∴PE=QE. ………………………………7 分
∵AE=GE, ∠AEG=90 , EQ⊥AG,
∴AG=2QE=2PE.
∵∠BEC=∠CBE=45 ,
∴BC=CE=EF.
∴MN=MH=PF. ………………………………9 分
1
∴BC-MN=EF-PF=PE= AG,
2

∴ = 1 = 2. ………………………………10 分
2
②S=961. ………………………………12 分
23.（13分）
（1） y = 2 . ………………………………1 分
（2）点 A的坐标是( √3, 3)，点 B的坐标是(√3, 3). ………………………………4 分
（3）解：如答图 1，过点 A作 AC⊥x轴于点 C，过点 B作 BD⊥x轴于点 D.
设点A( , 21 1 ), 点B( 2,
2
2 ), y
2
∵∠AOB=∠ACO=∠ODB=90 , y = x
∴∠AOC+∠BOD=90 , ∠AOC+∠OAC=90 ,
∴∠OAC=∠BOD, P B
A
∴△AOC∽△OBD. ………………………………5 分
C O D x
∴ = , 即 OC·OD=BD·AC,
答图 1
∴ 1 2 =
2
1
2
2 , 解得 1 2 = 1 或 1 2 = 0（舍去）. ……………………6 分
设直线 AB的解析式为y = kx + m(k ≠ 0).
= +
由{ 2 , 得
2 kx m = 0.
=
∵ 1 2 = = 1,
∴m=1.
∵当 x=0时，y=m=1,
∴点 P的坐标是（0，1）. ………………………………8 分
（4）①如答图 2，设抛物线的对称轴交 AB于点 D.
y
由抛物线和等腰直角三角形的对称性，
得 AD=BD, CD⊥AB, ∠DCB=∠DCA=45 ,
∴CD=BD=AD=a. ………………………………9 分 D
A O B x

∵对称轴为x = ,
2 C

∴点 B的坐标为（ + , 0)，点 C的坐标为（ ， ),
2 2
答图 2
将点 B, C的坐标分别代入y = 2 + + ，
2
0 = ( + ) + ( + ) +
得 { 2 22 ,解得 a=1或 a=0(舍去). ………………10 分
= ( ) + ( ) +
2 2
∴AB=2a=2, CD=1.
1 1
∴ △ABC = = × 2 × 1 = 1. ………………………………11 分 2 2
②c > 0 或 1 < c < 0. ………………………………13 分

展开更多......

收起↑