资源简介

2025年辽宁省抚顺市顺城区中考数学第一次质检试卷
一、选择题（本题共10小题，每小题3分，共30分.）
1．（3分）下列方程是一元二次方程的是（　　）
A．x2﹣2y+1＝0 B．3y2﹣2＝3（y2﹣2y）
C．ax2+bx+c＝0（a≠0） D．
2．（3分）剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
3．（3分）下列事件中，属于必然事件的是（　　）
A．任意画一个三角形，其外角和是360°
B．打开电视，正在播放跳水比赛
C．经过有交通信号的路口时遇见绿灯
D．若a＞b，则ac＞bc
4．（3分）近几年，二维码逐渐进入了人们的生活，成为广大民众生活中不可或缺的一部分，小刚将二维码打印在面积为20cm2的正方形纸片上，如图所示为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量重复实验发现点落在黑色阴影的频率稳定在0.6左右，则据此估计此二维码中黑色阴影的面积为（　　）
A．0.4cm2 B．0.6cm2 C．8cm2 D．12cm2
5．（3分）关于方程（x﹣2）2﹣1＝0根的情况，下列判断正确的是（　　）
A．有两个不相等的实数根
B．有两个相等的实数根
C．只有一个实数根
D．没有实数根
6．（3分）某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是91，求每个支干长出多少小分支．设每个支干长出x小分支，那么根据题意可以列方程为（　　）
A．1+x+x2＝91 B．1+x+x（1+x）＝91
C．1+x+（1+x）2＝91 D．1+（1+x）+（1+x）2＝91
7．（3分）抛物线y＝﹣3（x﹣2）2﹣1通过变换可以得到抛物线y＝﹣3x2+1，以下变换过程正确的是（　　）
A．先向左平移2个单位，再向上平移2个单位
B．先向左平移2个单位，再向下平移2个单位
C．先向右平移2个单位，再向下平移2个单位
D．先向右平移2个单位，再向上平移2个单位
8．（3分）如图，射线PA，PB切⊙O于点A，B，直线DE切⊙O于点C，交PA于点D，交PB于点E，若△PDE的周长是12cm，则PA的长是（　　）
A．3cm B．6cm C．12cm D．13cm
9．（3分）如图，△ABC中，∠BAC＝55°，将△ABC逆时针旋转α（0°＜α＜55°），得到△ADE，DE交AC于F．当α＝40°时，点D恰好落在BC上，此时∠AFE等于（　　）
A．80° B．85° C．90° D．95°
10．（3分）如表是一个二次函数的自变量x与函数值y的4组对应值：
x … ﹣1 1 2 4 …
y … ﹣7 3 5 3 …
下列说法：
①函数图象的开口向下；
②函数图象与x轴有两个交点；
③函数的最大值是5；
④当x＞3时，y的值随x值的增大而减小．正确说法的个数为（　　）
A．1个 B．2个 C．3个 D．4个
二、填空题（本题共5小题，每小题3分，共15分）
11．（3分）平面直角坐标系内一点P（﹣2，3）关于原点对称的点的坐标是 　 　．
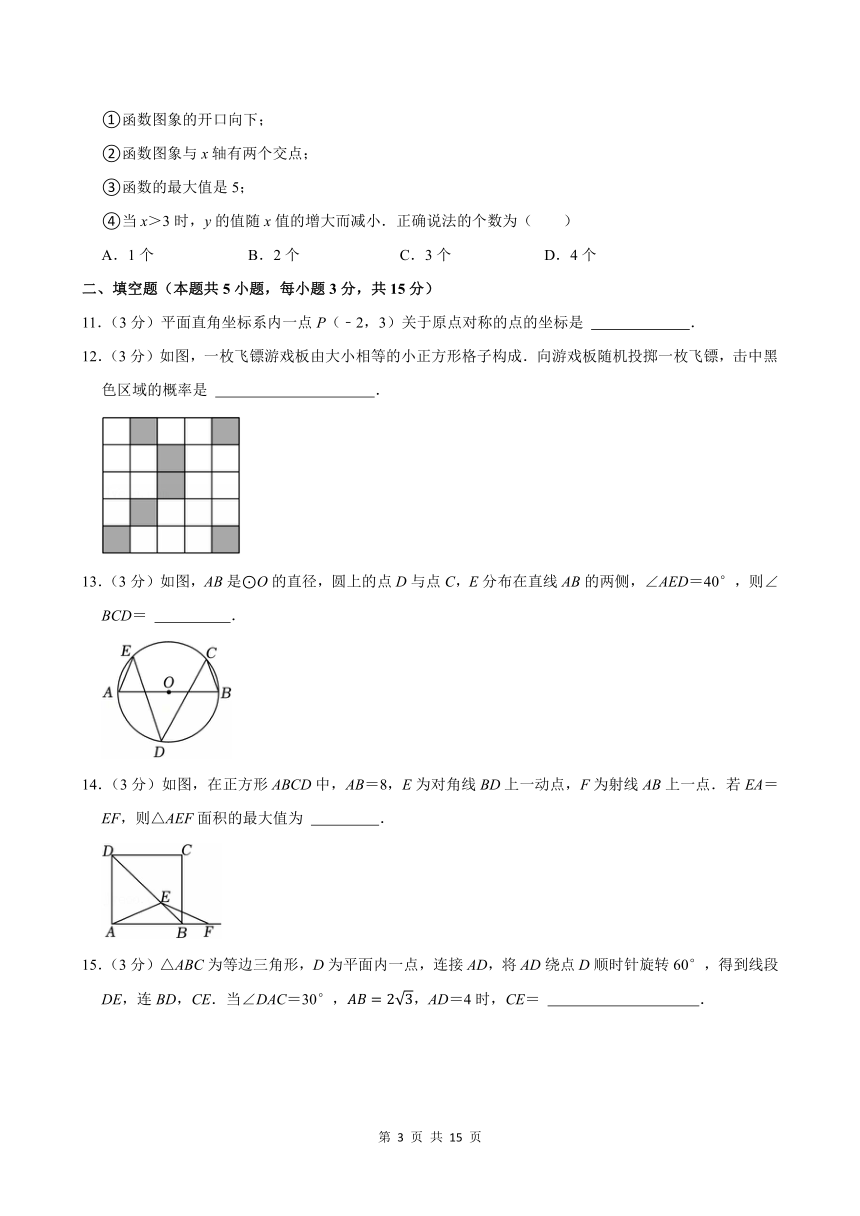
12．（3分）如图，一枚飞镖游戏板由大小相等的小正方形格子构成．向游戏板随机投掷一枚飞镖，击中黑色区域的概率是 　 　．
13．（3分）如图，AB是⊙O的直径，圆上的点D与点C，E分布在直线AB的两侧，∠AED＝40°，则∠BCD＝ 　 　．
14．（3分）如图，在正方形ABCD中，AB＝8，E为对角线BD上一动点，F为射线AB上一点．若EA＝EF，则△AEF面积的最大值为 　 　．
15．（3分）△ABC为等边三角形，D为平面内一点，连接AD，将AD绕点D顺时针旋转60°，得到线段DE，连BD，CE．当∠DAC＝30°，，AD＝4时，CE＝ 　 　．
三、解答题（本题共8小题，共75分，解答应写出文字说明、演算步骤或推理过程）
16．（10分）解下列方程：
（1）x2﹣6x﹣1＝0（配方法）；
（2）3x2﹣5x+1＝0（公式法）．
17．（7分）如图，在平面直角坐标系中，△ABC的三个顶点分别是A（1，3），B（4，4），C（2，1）．
（1）把△ABC向左平移4个单位后得到对应的△A1B1C1，请画出平移后的△A1B1C1；
（2）把△ABC绕原点O旋转180°后得到对应的△A2B2C2，请画出旋转后的△A2B2C2；
（3）观察图形可知，△A1B1C1与△A2B2C2关于点（ 　 　，　 　）中心对称．
18．（7分）某校利用“阳光体育大课间”对学校足球队全员进行定点射门训练，每人踢五次，训练结束后，把结果制成了如图所示不完整的折线统计图和扇形统计图．
（1）求此次定点射门训练中进球5次的人数；
（2）在此次定点射门训练中进球5次的队员中有1名女生．学校想从进球5次的队员中选2人参加比赛，请通过列表或画树形图的方法求参加比赛的队员是一男一女的概率．
19．（8分）李师傅去年开了一家商店，今年1月份开始盈利，2月份盈利2400元，4月份的盈利达到3456元，且从2月到4月，每月盈利的平均增长率都相同．
（1）求每月盈利的平均增长率；
（2）按照这个平均增长率，预计5月份这家商店的盈利将达到多少元？
20．（9分）某数学兴趣小组设计了一个投掷乒乓球游戏：将一个无盖的长方体盒子放在水平地面上，从箱外向箱内投乒乓球．建立如图所示的平面直角坐标系（长方形ABCD为箱子截面图，x轴经过箱子底面中心，并与其一组对边平行，AB＝CD＝1米，OB＝BC＝2米），王同学站在原点，将乒乓球从1.5米的高度P处抛出，乒乓球运行轨迹为抛物线，当乒乓球离王同学1米时，达到最大高度2米．
（1）求抛物线的解析式；
（2）王同学抛出的乒乓球能不能投入箱子，请通过计算说明；
（3）若乒乓球投入箱子后立即向右上方弹起，沿与原抛物线形状相同的抛物线运动，且无阻挡时乒乓球的最大高度达到原最大高度的一半，请判断乒乓球是否弹出箱子，并说明理由．
21．（10分）如图，△ABC是⊙O的内接三角形，∠C＝60°，点D在BO的延长线上，且AB＝AD．
（1）求证：DA是⊙O的切线；
（2）若⊙O的半径为2，求图中阴影部分的面积．（结果保留π和根号）
22．（12分）【问题背景】
在△ABC中，∠ACB＝90°，∠ABC＝α（0°＜α≤45°），点D，E分别在线段BC，AC上，将线段DE绕点D逆时针旋转180°﹣2α得到线段DF，点F落在线段AB上．
【问题初探】
（1）如图1，当α＝45°，点E与点C重合时，求证：FB＝FA；
【问题提升】
（2）如图2，当α＝45°，点E在线段AC上时，过点E作EG∥BC，交线段AB于点G，猜想线段AG与线段BF之间的数量关系，并证明；
【问题拓展】
（3）如图3，当α≠45°，点E在线段AC上时，过点E作FG∥BC，交线段AB于点G，（2）的结论是否成立，若成立，请证明，若不成立，请写出新的结论，并说明理由．
23．（12分）定义：在平面直角坐标系中，函数图象上到两个坐标轴的距离相等的点叫做这个函数图象的完美点．
【定义解析】
例如：函数上的点（2，2），到两个坐标轴的距离相等，我们就称点（2，2），是函数图象的完美点．
（1）若点（a+1，﹣2a）是一次函数y＝kx+4第四象限图象的完美点，求k的值；
（2）求二次函数y＝x2+x﹣4图象的完美点；
【定义应用】
（3）若二次函数y＝ax2﹣2x+c（a＞0）的图象上有且只有一个完美点（3，3），求二次函数的解析式；
【定义应用】
（4）若二次函数y＝（x﹣m）2+3m﹣2（m≥0）的图象上存在到两个坐标轴的距离相等且等于m的完美点，请直接写出m的值．
2025年辽宁省抚顺市顺城区中考数学第一次质检试卷
参考答案
一、选择题（本题共10小题，每小题3分，共30分.）
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D A A A B B C
二、填空题（本题共5小题，每小题3分，共15分）
11．答案为：（2，﹣3）．
12．答案为：．
13．答案为：50°．
14．答案为：16．
15．答案为：2或．
三、解答题（本题共8小题，共75分，解答应写出文字说明、演算步骤或推理过程）
16．解：（1）x2﹣6x﹣1＝0，
移项，得x2﹣6x＝1，
配方，得x2﹣6x+9＝10，
（x﹣3）2＝10．
∴x﹣3＝±．
∴x1＝3，x2＝3；
（2）3x2﹣5x+1＝0，
∵a＝3，b＝﹣5，c＝1，
∴Δ＝（﹣5）2﹣4×3×1＝13＞0，
∴x，
∴x1，x2．
17．解：（1）如图所示，△A1B1C1即为所求；
（2）如图所示，△A2B2C2即为所求；
（3）由图可得，△A1B1C1与△A2B2C2关于点（﹣2，0）中心对称．
故答案为：﹣2，0．
18．解：（1）进球4次的人数：12÷30%＝40（人）
进球5次的人数：40﹣1﹣9﹣15﹣12＝3（人）
答：进球5次的人数有3人．
（2）进球5次的人数有3人，其中女队员1人，所以男队员有2人．
男 男 女
男 （男，男） （女，男）
男 （男，男） （女，男）
女 （男，女） （男，女）
由表可知，一共有6种等可能结果，其中参加比赛的队员是一男一女的结果有：（女，男），（女，男），（男，女），（男，女）共4种．
∴概率．
19．解：（1）设该商店的每月盈利的平均增长率为x，根据题意得：
2400（1+x）2＝3456，
解得：x1＝20%，x2＝﹣2.2（舍去）．
（2）由（1）知，该商店的每月盈利的平均增长率为20%，则5月份盈利为：
3456×（1+20%）＝4147.2（元）．
答：（1）该商店的每月盈利的平均增长率为20%．
（2）5月份盈利为4147.2元．
20．解：（1）由题意得P（0，1.5），抛物线的顶点坐标为（1，2），
设抛物线的解析式为y＝a（x﹣1）2+2（a≠0），
∵抛物线y＝a（x﹣1）2+2经过点P（0，1.5），
∴1.5＝a+2，
∴a＝﹣0.5，
∴抛物线的解析式为y＝﹣0.5（x﹣1）2+2，即y＝﹣0.5x2+x+1.5；
（2）能，理由如下：
当x＝2时，y＝1.5＞AB，
当y＝0时，﹣0.5x2+x+1.5＝0，
解得x1＝﹣1（舍去），x2＝3，
∴乒乓球在运行中，高于AB，并落在BC的中点处，
∴王同学抛出的乒乓球能投入箱子；
（3）解：乒乓球不能弹出箱子．理由如下：
依题意，设乒乓球弹出后的抛物线解析式为y＝﹣0.5（x﹣k）2+1，
∵抛物线y＝﹣0.5（x﹣k）2+1的图象经过点（3，0），
∴﹣0.5（3﹣k）2+1＝0，
解得（舍去），，
∴弹出后抛物线解析式为，
当x＝4时，，
∴乒乓球不能弹出箱子．
21．（1）证明：如图，连接OA，
∵∠C＝60°，
∴∠AOB＝120°，
∵OA＝OB，
∴∠OBA＝∠OAB，
∵在△AOB中，∠AOB+∠OBA+∠OAB＝180°，
∴∠OBA＝∠OAB＝30°，
∵AB＝AD，
∴∠ABD＝∠ADB＝30°，
由条件可知∠BAD＝120°，
∵∠BAD＝∠OAB+∠OAD，
∴∠OAD＝90°，
即OA⊥AD，
∵OA是半径，
∴DA是⊙O的切线；
（2）解：过点O作OE⊥AB，垂足为点E
∴∠OEB＝90°，AB＝2BE，
∵在Rt△OEB中，∠OBE＝30°，OB＝2，
∴OE＝1，
∴BE2＝22﹣12＝3，
∴，
∴，
∴，
∵，
∴，
答：图中阴影部分的面积为．
22．（1）证明：如图1，连接EF，
当α＝45°，点E与点C重合时，∠ABC＝45°，∠EDF＝180°﹣2α＝90°，
由旋转可得DE＝DF，
∴△DEF是等腰直角三角形，
∴∠DEF＝∠DFE＝45°，
∴∠DEF＝∠ABC＝45°，
∴FB＝FE，
∵∠ACB＝90°，
∴∠AEF＝∠BAC＝45°，
∴FA＝FE，
∴FB＝FA；
（2）解：AG＝2BF；
证明：如图2，过点D作DM⊥BC，交AB于点M，连接EM，
∴∠MDB＝90°，
∵当α＝45°，点E在线段AC上时，∠ABC＝45°，∠EDF＝180°﹣2α＝90°，
∴∠BMD＝45°，∠MDB＝∠EDF＝90°，
∴∠ABC＝∠BMD＝45°，
∴DM＝DB，∠EDM＝∠FDB，
由旋转可得DE＝DF，
在△EDM和△FDB中，
，
∴△EDM≌△FDB（SAS），
∴ME＝BF，∠DME＝∠DBF＝45°，
∴∠GME＝∠DMB+∠DME＝90°，
∵EG∥BC，
∴∠AGE＝∠ABC＝45°，∠AEG＝∠ACB＝90°，
∴∠MGE＝∠MEG＝45°，∠MAE＝∠MEA＝45°，
∴MG＝ME，MA＝ME，
∴AG＝2ME，
∴AG＝2BF；
（3）解：成立；
证明：如图，在线段上取点M，使DM＝DB，取AG中点N，连接EM，EN，
∴∠DMB＝∠DBM＝α，AG＝2NE，
∴∠MDB＝180°﹣2α，
∴∠MDB＝∠EDF，
∴∠EDM＝∠FDB，
由旋转可得DE＝DF，
在△EDM和△FDB中，
，
∴△EDM≌△FDB（SAS），
∴ME＝BF，∠DME＝∠DBF＝α，
∴∠BME＝2α，
∵EG∥BC，
∴∠AGE＝∠ABC＝α，∠AEG＝∠ACB＝90°，
∵N是AG的中点，
∴NG＝NE，AG＝2NE，
∴∠NGE＝∠NEG＝α，
∴∠ENM＝2α，∠ENM＝∠BME＝2α，
∴NE＝ME，
∴AG＝2BF．
23．解：（1）∵点（a+1，﹣2a）是一次函数y＝kx+4（k≠0）第二象限图象的完美点，
∴a+1﹣2a＝0，
解得：a＝1，
∴点（a+1，﹣2a）的坐标为（2，﹣2），
将（2，﹣2）代入y＝kx+4得：
﹣2＝2k+4，
解得：k＝﹣3；
（2）∵完美点是函数图象上到两坐标轴的距离相等的点，即完美点在直线y＝x或直线y＝﹣x上，
联立得：，
解得，；
或联立得：，
解得，，
∴二次函数y＝x2+x﹣4图象的完美点分别是：（2，2），（﹣2，﹣2），，；
（3）∵二次函数y＝ax2﹣2x+c（a＞0）的图象上有且只有一个完美点（3，3），
在直线y＝x上，
∴，
∴ax2﹣3x+c＝0有且只有一个完美点，
∴Δ＝32﹣4ac＝0，
把点（3，3）代入y＝ax2﹣2x+c，得9a﹣6+c＝3，
解得：，，
∴；
（4）∵二次函数y＝（x﹣m）2+3m﹣2（m≥0）的图象上存在到两个坐标轴的距离相等且等于m的完美点，即完美点在直线y＝x或直线y＝﹣x上，
①当时，（x﹣m）2+3m﹣2＝x，
整理得：x2﹣（2m+1）x+m2+3m﹣2＝0有实数根，
∴Δ＝（2m+1）2﹣4（m2+3m﹣2）＝﹣8m+9≥0，
∴，
∵m≥0，
∴，
当x＝m时，y＝x＝m，如图1，
将（m，m）代入y＝（x﹣m）2+3m﹣2，
解得m＝1，
当x＝﹣m时，y＝x＝﹣m，如图2，
将（﹣m，﹣m）代入y＝（x﹣m）2+3m﹣2，
解得（舍去），，
∵|x|＝m，
∴或m＝1；
②当时，如图3，（x﹣m）2+3m﹣2＝﹣x，
整理得x2﹣（2m﹣1）x+m2+3m﹣2＝0有实数根，
∴Δ＝（2m﹣1）2﹣4（m2+3m﹣2）＝﹣16m+9≥0，
∴，
∵m≥0，
∴，
当x＝m时，y＝﹣x＝﹣m，
将（m，﹣m）代入y＝（x﹣m）2+3m﹣2，
解得，
当x＝﹣m时，y＝﹣x＝m，
将（﹣m，m）代入y＝（x﹣m）2+3m﹣2，
解得，（舍去），，
∵|x|＝m，
∴，
综上所述，或m＝1或．

展开更多......

收起↑