资源简介

中小学教育资源及组卷应用平台
第十八章平行四边形期中复习解答题压轴题练习人教版2024—2025学年八年级下册
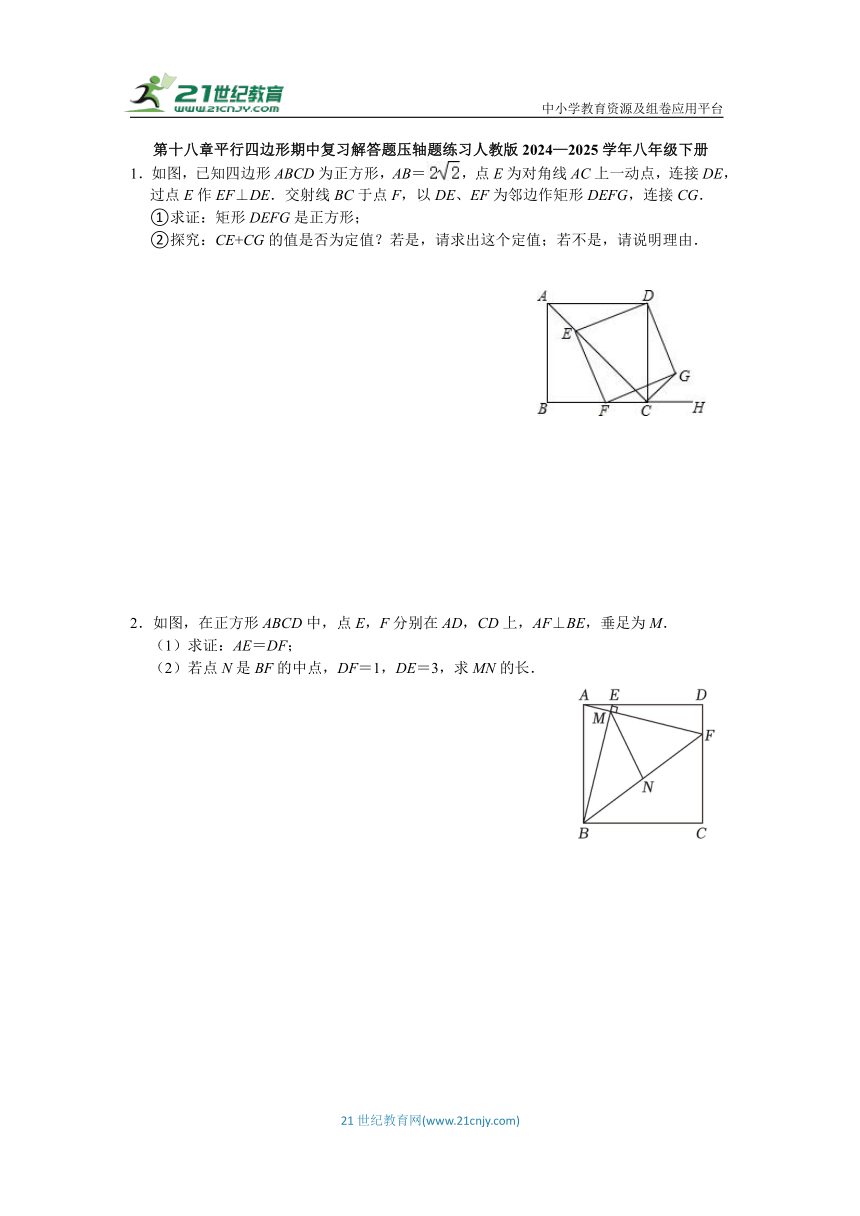
1．如图，已知四边形ABCD为正方形，AB＝，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE．交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
①求证：矩形DEFG是正方形；
②探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．
2．如图，在正方形ABCD中，点E，F分别在AD，CD上，AF⊥BE，垂足为M．
（1）求证：AE＝DF；
（2）若点N是BF的中点，DF＝1，DE＝3，求MN的长．
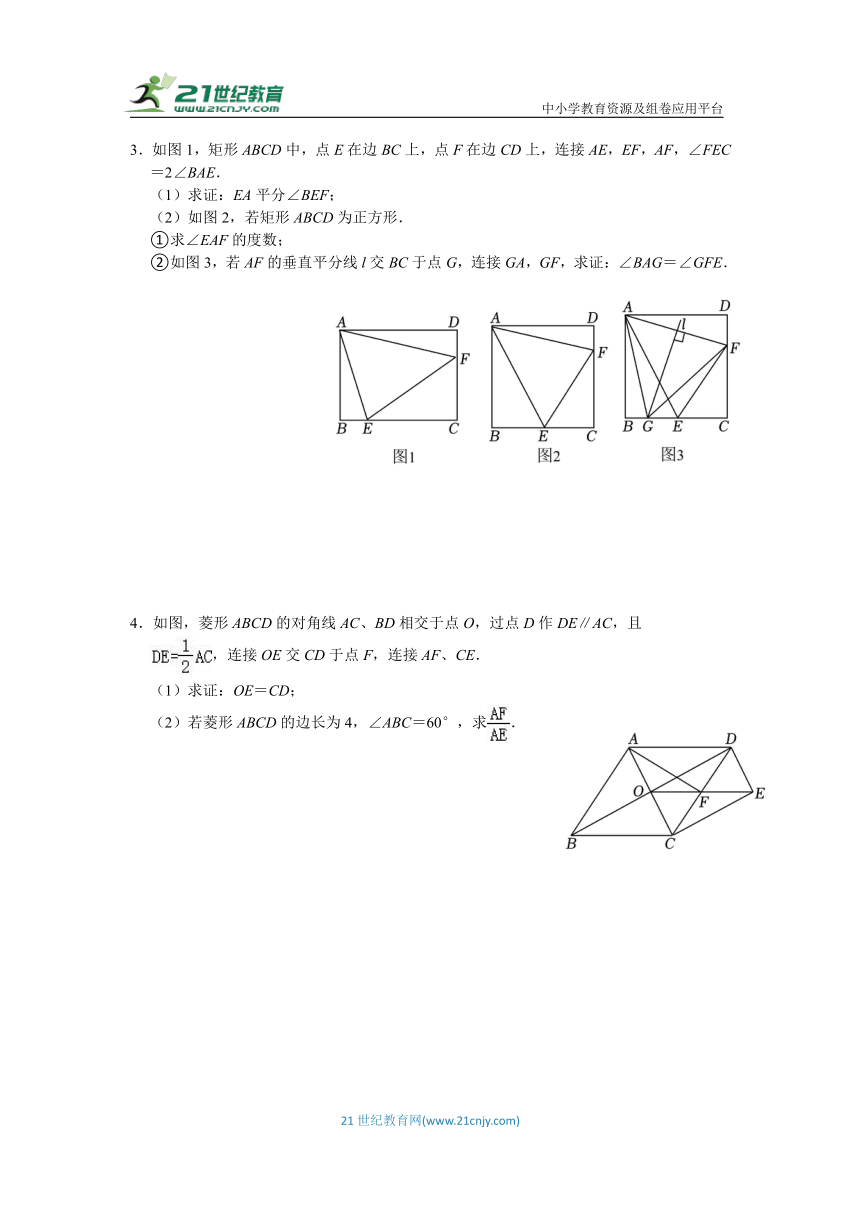
3．如图1，矩形ABCD中，点E在边BC上，点F在边CD上，连接AE，EF，AF，∠FEC＝2∠BAE．
（1）求证：EA平分∠BEF；
（2）如图2，若矩形ABCD为正方形．
①求∠EAF的度数；
②如图3，若AF的垂直平分线l交BC于点G，连接GA，GF，求证：∠BAG＝∠GFE．
4．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且
，连接OE交CD于点F，连接AF、CE．
（1）求证：OE＝CD；
（2）若菱形ABCD的边长为4，∠ABC＝60°，求．
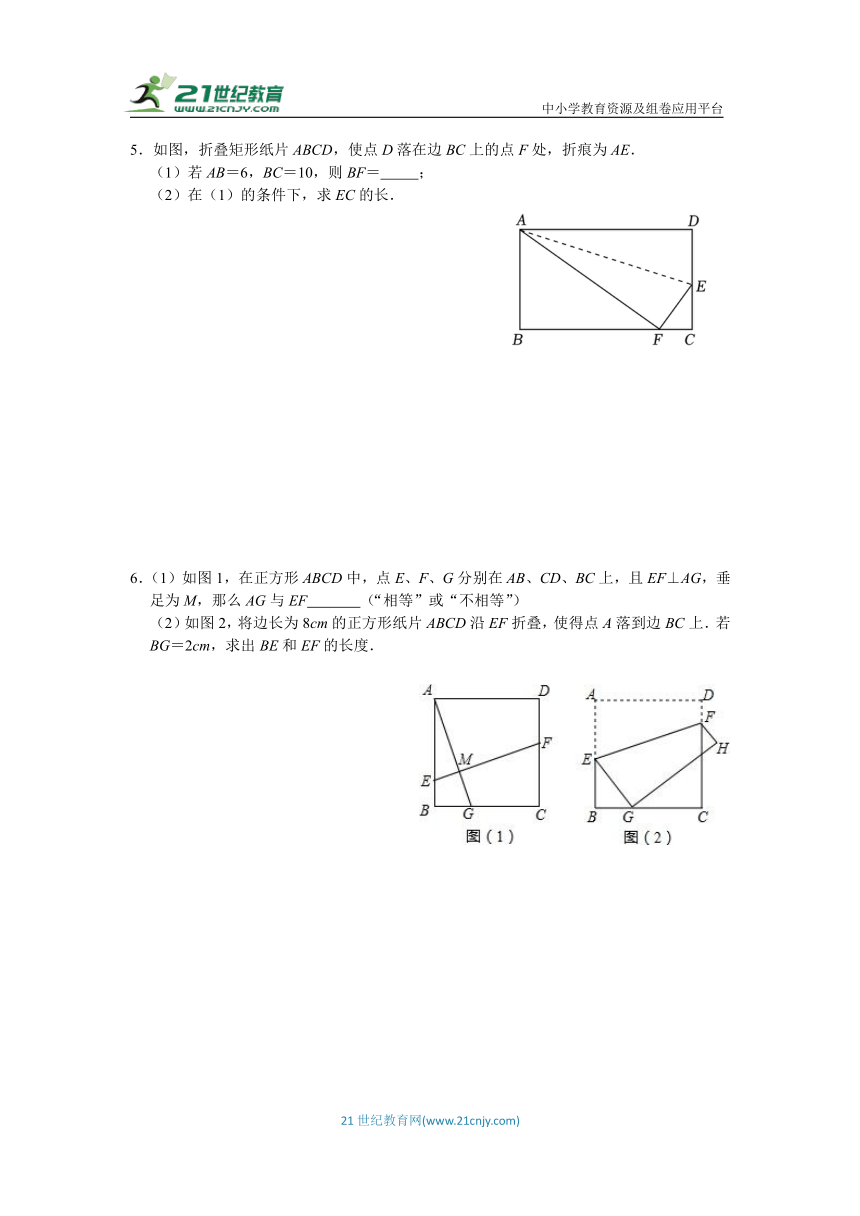
5．如图，折叠矩形纸片ABCD，使点D落在边BC上的点F处，折痕为AE．
（1）若AB＝6，BC＝10，则BF＝　 　；
（2）在（1）的条件下，求EC的长．
6．（1）如图1，在正方形ABCD中，点E、F、G分别在AB、CD、BC上，且EF⊥AG，垂足为M，那么AG与EF　 　（“相等”或“不相等”）
（2）如图2，将边长为8cm的正方形纸片ABCD沿EF折叠，使得点A落到边BC上．若BG＝2cm，求出BE和EF的长度．
7．已知：矩形ABCD，AC、BD交于点O，过点O作EF⊥BD分别交AB、CD于E、F．
（1）求证：四边形BEDF是菱形．
（2）若BC＝3，CD＝5，求S菱形BEDF．
8．如图，正方形ABCD中，AB＝6，点E在CD边上运动（不与点C、D重合）．过点B作AE的平行线交DC的延长线于点F，过点D作AE的垂线DN分别交于AE，BF于点M、N．
（1）求证：四边形ABFE是平行四边形；
（2）若，求线段MN的长；
（3）点E在CD边上运动过程中，∠CND的大小是否改变？若不变，求出该值，若改变请说明理由．
9．如图，正方形ABCD的边长为6，点E是BC的中点，连接AE与对角线BD交于点G，连接CG并延长，交AB于点F，连接DE交CF于点H，连接AH．
（1）求证：∠AEB＝∠DEC；
（2）求证：CF⊥DE；
（3）求线段HF的长．
10．如图，在正方形ABCD中，点E在边BC上，点F在边AD的延长线上，连接EF与边CD相交于点G，连接AE、BD，DF＝DG，EA＝EG．
（1）求证：四边形BDFE是平行四边形；
（2）求∠AEG大小；
（3）若AE＝6，求 BDFE的面积．
11．如图，在 ABCD中，AD＝2CD，F是AD的中点，CE⊥AB，垂足为点E，连接EF、CF．
（1）求证：CF平分∠BCD；
（2）若BE＝5，CE＝12，求△ECF的面积；
（3）请判断线段EF与CF的数量关系，并说明理由．
12．如图1，四边形ABCD是正方形，点E在正方形外角的平分线上，连接AE，记AE与对角线BD的交点为M．
（1）求证：AM＝EM；
（2）如图2，点N是边AB的中点，连接MN，若MN＝AN，请探索BE与BD的数量关系，并说明理由；
（3）如图3，在（2）的条件下，记BE与边CD的交点为点F，在BC边上取点P，使BP+DE＝PF，连接AP，AF，求∠PAF的度数．
13．如图，已知△ABC．
（1）尺规作图：作平行四边形ABCD；（保留作图痕迹，不写作法）
（2）在（1）所作的平行四边形ABCD中，连接BD，交AC于点O．
①若∠BAC＝90°，AB＝8，AC＝12，求BD的长；
②过点O作直线EF与边AD，BC分别交于点E，F，设四边形EDCF的面积为S1，平行四边形ABCD的面积为S2，求S1：S2的值．
14．如图，点E在正方形ABCD对角线BD上，连接AE、CE，点F为AB上一点，连接CF，
交BD于点G．连接EF，若AE＝EF．
（1）求证：AE＝CE；
（2）求∠ECF的度数；
（3）经探究，DE、BG、EG三条线段满足某种数量关系，请直接写出们之间的关系式．
15．如图，直线y＝kx﹣4k（k≠0）与坐标轴分别交于点A，B，过点A、B作直线AB，以OA为边在y轴的右侧作四边形AOBC，S△AOB＝8．
（1）求点A，B的坐标；
（2）如图，点D是x轴上一动点，点E在AD的右侧，∠ADE＝90°，AD＝DE；
①如图1，问点E是否在定直线上，若是，求该直线的解析式；若不是，请说明理由；
②如图2，点D是线段OB的中点，另一动点H在直线BE上，且∠HAC＝∠BAD，请直接写出点H的坐标．
参考答案
1．【解答】①证明：过E作EM⊥BC于M点，过E作EN⊥CD于N点，如图所示：
∵正方形ABCD，
∴∠BCD＝90°，∠ECN＝45°，
∴∠EMC＝∠ENC＝∠BCD＝90°，
且NE＝NC，
∴四边形EMCN为正方形，
∵四边形DEFG是矩形，
∴EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，
∴∠DEN＝∠MEF，
又∠DNE＝∠FME＝90°，
在△DEN和△FEM中，，
∴△DEN≌△FEM（ASA），
∴ED＝EF，
∴矩形DEFG为正方形；
②解：CE+CG的值为定值，理由如下：
∵矩形DEFG为正方形，
∴DE＝DG，∠EDC+∠CDG＝90°，
∵四边形ABCD是正方形，
∴AD＝DC，∠ADE+∠EDC＝90°，
∴∠ADE＝∠CDG，
在△ADE和△CDG中，，
∴△ADE≌△CDG（SAS），
∴AE＝CG，
∴AC＝AE+CE＝AB＝×2＝4，
∴CE+CG＝4 是定值．
2．【解答】（1）证明：∵四边形ABCD是正方形，
∴∠BAE＝∠D＝90°，AB＝DA，
∴∠DAF+∠BAF＝90°，
∵AF⊥BE，
∴∠ABE+∠BAF＝90°，
∴∠ABE＝∠DAF，
在△ABE和△DAF中，
，
∴△ABE≌△DAF（ASA），
∴AE＝DF；
（2）解：∵AE＝DF＝1，DE＝3，
∴AD＝CD＝BC＝AE+DE＝4，CF＝CD﹣DF＝4﹣1＝3，
∴BF＝＝＝5，
∵AF⊥BE，点N是BF的中点，
∴MN＝BF＝2.5．
3．【解答】（1）证明：作EH平分∠FEC，交CD于点H，
∴，
∵∠FEC＝2∠BAE，
∴∠FEH＝∠CEH＝∠BAE，
∵矩形ABCD中，∠B＝90°，
∴∠AEB+∠BAE＝90°，
∴∠AEB+∠CEH＝90°，
∴∠AEF+∠FEH＝90°，
∴∠AEB＝∠AEF，即EA平分∠BEF；
（2）①过点A作AR⊥EF于点R，
∵四边形ABCD是正方形，
∴AB＝AD，∠B＝∠ARE＝90°，
由（1）得∠AEB＝∠AEF，
又∵AE＝AE，
∴△EAB≌△EAR，
∴AB＝AR，∠BAE＝∠RAE，
∴AD＝AR，
∵AF＝AF，∠D＝∠FRA＝90°，
∴△FAD≌△FAR，
∴∠FAD＝∠FAR，
∴；
②过点A作AW⊥EF，在EF上截取ET＝EG，
∵ET＝EG，∠AEG＝∠AET，AE＝AE，
∴△AEG≌△AET，
∴∠2＝∠3，AG＝AT，∠AGE＝∠ATE，
∴∠AGB＝∠ATW，
∴∠1＝∠4
∵AF的垂直平分线l交BC于点G，
∴∠5+∠GAF＝90°
∵∠EAF＝45°，
∴∠5+∠2＝45°，
∴2∠5+2∠2＝90°，即∠AGF+∠GAQ＝90°，
∴∠AQG＝90°，
∴∠AQP＝90°＝∠AWF，
∵∠APQ＝∠FPW，
∴∠PFW＝∠4
∴∠GFE＝∠1，即∠BAG＝∠GFE．
4．【解答】（1）证明：四边形ABCD是菱形，
∴OA＝OC＝AC，AD＝CD，
∵DE∥AC且DE＝AC，
∴DE＝OA＝OC，
∴四边形OADE、四边形OCED都是平行四边形，
∴OE＝AD，
∴OE＝CD；
（2）解：连接AE．
∵AC⊥BD，
∴四边形OCED是矩形，
∴CF＝DF，
∵在菱形ABCD中，∠ABC＝60°，
∴AC＝AB＝CD＝AD＝4，
∴AF⊥CD，
∴AF＝＝＝2，
在矩形OCED中，CE＝OD＝＝2．
在Rt△ACE中，AE＝＝＝2．
∴＝＝，
5．【解答】解：（1）∵四边形ABCD是长方形，
∴AD＝BC＝10，CD＝AB＝6，
∵长方形纸片沿AE折叠，点D落在BC边的点F处，
∴AF＝AD＝10，EF＝DE，
在Rt△ABF中，；
（2）由（1）知BF＝8，
∴FC＝BC﹣BF＝10﹣8＝2，
设DE＝x，则EC＝CD﹣DE＝6﹣x，
在Rt△CEF中，EC2+FC2＝EF2，
即（6﹣x）2+22＝x2，
解得，
∴．
6．【解答】解：（1）如图（1）所示，过点E作EH∥AD，交CD于H；则四边形AEHD为矩形；
∴EH＝AD＝AB；
∵AG⊥EF，EH∥AD，
∴∠BAG+∠AEF＝90°，∠AEF+∠FEH＝90°，
∴∠BAG＝∠FEH；在△ABG与△EHF中，
∵，∴△ABG≌△EHF（ASA）
∴AG＝EF．
故答案为相等；
（2）如图（2），连接AG；
设BE＝x，则AE＝8﹣x；由对称原理得：EG＝EA＝8﹣x，∠AEF＝∠GEF，
∴EF⊥AG；由问题（1）知：EF＝AG；
∵四边形ABCD为正方形，∴∠EBG＝90°；
由勾股定理得：AG2＝82+22，AG＝；
（8﹣x）2＝x2+22，解得x＝，
∴BE＝（cm），EF＝（cm）．
7．【解答】（1）证明：∵四边形ABCD是矩形，
∴AB∥CD，OB＝OD，
∴∠EBD＝∠FDB，
在△EBO和△FDO中，
，
∴△EBO≌△FDO（ASA），
∴OE＝OF，
∵OB＝OD，
∴四边形BEDF是平行四边形，
∵EF⊥BD，
∴四边形BEDF是菱形；
（2）解：∵四边形ABCD是矩形，
∴∠BCD＝90°，
∵四边形BEDF是菱形，
∴BF＝DF，
∵BC＝3，CD＝5，
∴FC＝CD﹣DF＝5﹣BF，
在Rt△BCF中，根据勾股定理得：
BF2＝BC2+FC2，
∴BF2＝32+（5﹣BF）2，
∴BF＝，
∴S菱形BEDF＝DF BC＝BF BC＝×3＝．
8．【解答】（1）证明：∵四边形ABCD是正方形，
∴AB∥DC，
∵AE∥BF，
∴四边形ABFE是平行四边形；
（2）解：在正方形ABCD中，AB＝6，
∴BC＝CD＝AD＝AB＝6，∠ADC＝∠BCD＝90°，
∵，
∴DE＝2，CE＝4，
∴AE＝2，
对于△AED，∠ADE＝90°，DM⊥AE，
∴AD DE＝AE DM，
解得DM＝．
连接BD，
∵AE∥BF，
∴DN⊥BF，
∴∠DNF＝90°．
∴BC DF＝BF DN，
由（1）知，四边形ABFE是平行四边形，
∴EF＝AB＝6，BF＝AE＝2，
∴DF＝8，
∴6×8＝2 DN，
∴DN＝．
∴MN＝DN﹣DM＝．
（3）不变，∠CND＝45°，理由如下：
如图，在DN上取点G，使DG＝BN，连接CG，CN，
∵∠NDF+∠F＝∠CBF+∠F＝90°，
∴∠NDF＝∠CBF，
∵DC＝BC，DG＝BN，
∴△CDG≌△CBN（SAS），
∴CG＝CN，∠DCG＝∠BCN，
∵∠DCG+∠BCG＝90°，
∴∠BCN+∠BCG＝90°，即∠GCN＝90°．
∴∠CNG＝45°，即∠CND＝45°．
9．【解答】（1）证明：∵四边形ABCD是边长为6的正方形，
∴∠DCE＝∠ABE＝90°，AB＝CD，
∵点E是BC的中点，
∴BE＝CE＝3，
∴△ABE≌△DCE（SAS），
∴∠DEC＝∠AEB；
（2）证明：在正方形ABCD中，AB＝BC，∠ABG＝∠CBG＝45°，
∵BG＝BG，
∴△ABG≌△CBG（SAS），
∴∠BAE＝∠BCF，
∵∠DEC＝∠AEB，
∴∠CHD＝∠BCF+∠DEC
＝∠BAE+∠AEB
＝∠ABE
＝90°，
∴CF⊥DE；
（3）解：∵∠CDE＝∠BCF，DC＝BC，∠DCE＝∠CBF＝90°°，
∴△DCE≌△CBF（ASA），
∴DE＝CF，
∵，
在Rt△DCE，根据勾股定理得：
，
∴，
∵，
∴6×3＝3CH，
∴，
∴．
10．【解答】解：（1）∵四边形ABCD是正方形，
∴AD∥BC，∠CBD＝45°，∠ADC＝90°，
∴∠CEG＝∠F，∠FDG＝90°，
∵DF＝DG，
∴∠DGF＝∠F＝45°，
∴∠CEG＝45°，
∴∠CBD＝∠CEG，
∴BD∥EF，
∴四边形BDFE是平行四边形；
（2）连接AG，
∵四边形BDFE是平行四边形，
∴BE＝DF＝DG，
∵四边形ABCD是正方形，
∴∠ABE＝∠ADC＝90°，AB＝AD，
在△ABE与△ADG中，
，
∴△ABE≌ADG（SAS），
∴AE＝AG；
又∵AE＝EG，
∴AE＝AG＝EG，
∴△AEG是等边三角形，
∴∠AEG＝60°；
（3）∵∠CEG＝45°，∠C＝90°，
∴CE＝CG，
∵EG＝AE＝6，
∴CE＝，
∴AB＝BC＝BE+，
∵AB2+BE2＝AE2，
∴（BE+）2+BE2＝62，
化简得：BE2+BE＝9，
∴S BDFE＝BE AB＝BE （BE+）＝BE2+BE＝9，
11．【解答】（1）证明：∵AD＝2CD，F是AD的中点，
∴AF＝DF＝CD，
∴∠DFC＝∠DCF，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴∠DFC＝∠BCF，
∴∠DCF＝∠BCF，
∴CF平分∠BCD；
（2）解：如图，延长CD、EF交于点G，
∵AB∥CD，
∴∠A＝∠FDG，∠BEC＝∠ECD＝90°，
∵F是AD的中点，
∴AD＝DF，
在△AEF和△DGF中，
，
∴△AEF≌△DGF（ASA），
∴EF＝GF，AE＝DG，
∵BE＝5，CE＝12，
∴BC＝＝＝13，
∵BC＝AD＝2CD，
∴CD＝AB＝，
∴CG＝CD+DG＝CD+AE＝CD+AB﹣BE＝13﹣5＝8，
∴S△ECG＝×EC CG＝48，
∵EF＝FG，
∴S△EFC＝S△ECG＝24．
（3）解：EF＝CF，理由如下：
∵EF＝FG，∠ECD＝90°，
∴EF＝FC．
12．【解答】（1）证明：∵四边形ABCD为正方形，
∴AD＝CD，∠ADC＝90°，DM平分∠ADC，
∴∠ADM＝∠CDM＝45°，
∴△ADM≌△CDM（SAS），
∴AM＝CM，
∴∠MAC＝∠MCA，
∵点E在正方形外角的平分线上，
∴∠DCE＝45°，
又∵∠ACD＝45°，
∴∠ACE＝90°，
∴∠EAC+∠E＝90°，∠MCA+∠MCE＝90°，
∴∠E＝∠MCE，
∴ME＝CM，
∴AM＝ME；
（2）解：BE＝BD，
理由：∵N为AB的中点，AM＝ME，
∴MN为△ABE的中位线，
∴MN＝BE，
∵MN＝AN，
∴BE＝2AN，
又∵AB＝AD，
∴BD＝AB，
∵AB＝2AN，
∴BD＝2AN，
∴BD＝BE；
（3）解：连接AC交BD于点O，过点E作EG⊥BD于点G，则四边形OCEG为矩形，
∴OC＝EG，
∵OA＝AC＝BD，BE＝BD，
∴EG＝BE，
∴∠GBE＝30°，
∵BD＝BE，
∴∠BDE＝∠BED＝75°，
又∵∠BDC＝45°，
∴∠FDE＝30°，
∴∠DFE＝180°﹣∠FDE﹣∠DEB＝75°，
∴∠DFE＝∠DEF，
∴DF＝DE，
延长PB到H，使BH＝DF，连接AH，PF，则BH＝DE，
∵AD＝AB，∠ADF＝∠ABH＝90°，
∴△ADF≌△ABH（SAS），
∴AF＝AH，∠FAD＝∠HAB，
∴∠HAF＝∠HAB+∠BAF＝∠FAD+∠BAF＝90°，
∵PF＝DE+BP，PH＝BH+PB＝DE+PB，
∴PF＝PH，
又∵AP＝AP，
∴△APH≌△APF（SSS），
∴∠PAH＝∠PAF，
∴∠PAF＝∠HAC＝45°．
13．【解答】解：（1）如图1所示，
ABCD即为所求；
（2）①如图2，
∵四边形ABCD是平行四边形，AC＝12，
∴BD＝2BO，AO＝AC＝×12＝6，
∵∠BAC＝90°，AB＝8，
∴BO＝＝＝10，
∴BD＝2BO＝2×10＝20；
②如图3，
∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝CB，
∵BD＝DB，
∴△ABD≌△CDB（SSS），
∴S△ABD＝S△CDB，
∴，
∵四边形ABCD是平行四边形，
∴AD∥BC，BO＝DO，
∴∠OED＝∠OFB，∠ODE＝∠OBF，
∴△OED≌△OFB（AAS），
∴S△OED＝S△OFB，
∴S四边形EDCF＝S△OED+S四边形ODCF＝S△OBF+S四边形ODCF＝S△BCD，
∴，
∴S1：S2＝．
14．【解答】（1）证明：∵四边形ABCD是正方形，
∴∠ADE＝∠CDE＝45°，
∵DA＝DC，DE＝DE，
∴△ADE≌△CDE（SAS），
∴AE＝CE．
（2）解：∵EA＝EF，
∴∠EAF＝∠EFA．
设∠DCE＝∠DAE＝x，则∠DEC＝∠DEA＝135°﹣x，∠EAF＝∠EFA＝90°﹣x，
∴∠AEF＝180°﹣2∠EAF＝2x，
∴∠FEC＝360°﹣2∠DEC﹣∠AEF＝90°．
∵EF＝EC，
∴∠ECF＝＝45°．
（3）解：GE2＝BG2+ED2，证明如下，
将△BCG绕点C顺时针方向旋转90°得到△DCG'，连接EG'，
∵∠ECF＝45°，
∴∠ECG'＝∠DCG'+∠ECD＝∠BCG+∠ECD＝45°＝∠ECG，
∵GC＝G'C，EC＝EC，
∴△GCE≌△G'CE（SAS），
∴EG＝EG'．
∵∠EDG'＝∠EDC+∠G'DC＝45°+45°＝90°，
∴ED2+G'D2＝G'E2，
即GE2＝BG2+ED2．
15．【解答】解：（1）分别将x＝0，y＝0代入y＝kx﹣4k（k≠0），
得y＝﹣4k，x＝4，
即A（0，﹣4k），B（4，0），
∴OA＝﹣4k，OB＝4，
∵，
∴k＝﹣1，
即A（0，4），B（4，0）．
答：A（0，4），B（4，0）．
（2）①点E是在定直线上．
过点E作EF⊥x轴，如图，
由题意可得：∠AOD＝∠DFE＝∠ADE＝90°，
∴∠ADO+∠EDF＝∠ADO+∠OAD＝90°，
∴∠OAD＝∠EDF，
∴△AOD≌△DFE（AAS），
∴DF＝OA＝4，EF＝OD，
∴BF＝DF﹣DB＝OA﹣DB＝OB﹣DB＝OD，
∴EF＝BF，
设E（x，y），则D（y，0），F（x，0），
由题意可得：OF＝OD+DF＝OD+OA，
即y＝x﹣4，
∴点E在定直线y＝x﹣4上．
②连接AE，由题意可得△ADE为等腰直角三角形，∠DAE＝45°，
∵四边形OACB为正方形，
∴∠BAC＝∠DAE＝45°，
∴∠EAC＝∠BAD，此时点H与点E重合，
由①可得E（6，2），
∴H（6，2），
设直线AE为y＝kx+b，将E（6，2）、A（0，4）代入，
得，
解得，
∴直线AE为，
当x＝4时，，
∴，
作点M关于直线AC的对称点N，
∴，
此时∠NAC＝∠EAC＝∠BAD，
∴点H为直线AN与BE的交点，
∴直线AN为，
联立，
解得，
∴H（12，8）．
综上，点H坐标为（12，8）或（6，2）．
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑