资源简介

中小学教育资源及组卷应用平台
第三单元运算律（知识梳理+拔高训练）一
知识梳理
知识点一：加法运算定律
1.加法交换律：两个数相加，交换加数的位置，和不变，用字母表示为：a＋b=b＋a。
2.若干个数相加，任意交换加数的位置，和不变。
3.加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。用字母表示为 （a+b）+c=a+(b+c).
4.加法结合律经常与加法交换律一起使用，这样可以使几个数相加时，能凑成整十、整百、整 千……的数，先交换再结合这样计算比较简便。
5.在一个连加算式中，运用加法运算定律，把能凑成整十、整百、整千……的数先相加，可以使计算简便。
6.加法交换律改变的是加数的位置，加法结合律改变的是运算顺序。
7.加法结合律的重要标志是小括号的使用。
8.在一个连加算式中，运用加法运算定律，把能凑成整十、整百、整千……的数先相加，可以使计算简便。
9.在连减运算中，交换两个减数的位置，差不变。用字母表示为：a－b－c＝a－c－b。
10.一个数连续减去两个数，等于这个数减去这两个数的和。用字母表示为：a－b－c＝a－(b＋c)。
知识点二：乘法运算定律
1.乘法交换律
（1）两个数相乘，交换两个因数的位置，积不变。
（2）乘法交换律用字母表示为：a×b＝b×a。
（3）多个数相乘，任意交换因数的位置，积不变。
2.乘法结合律
（1）三个数相乘，先乘前两个数，或者先乘后两个数，积不变。字母表示为：（a×b）×c＝a×（b×c）
（2）在运用乘法运算定律进行简算时，有时会同时用到乘法交换律和乘法结合律。
3.乘法分配律
（1）两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。用字母表示为：(a ＋ b)×c=a×c ＋ b×c。
（2）两个数的差与一个数相乘，可以先把被减数和减数分别与这个数相乘，再把所得的积相减。用字母表示为：(a － b)×c=a×c － b×c。
3.乘、除法的简便运算
（1）乘法的简便算法：两个数相乘，如果其中一个因数是25（或125），可考虑将另一个因数分解成4×（ ）或8×（ ），再运用乘法结合律进行简便计算；如果其中一个因数接近整十数、整百数、整千数……可将其分解成10±（ ）、100±（ ）、1000±（ ） ……再运用乘法分配律进行简便计算。
（2）除法的运算性质：一个数连续除以两个数，等于这个数除以这两个数的积。用字母表示为：a÷b÷c＝a÷（b×c）。
拔高训练
一、填空题（共20分）
1．（2分）观察如图的竖式，在这个竖式计算过程中运用了( )律，用横式表示下边的竖式是( )。
2．（2分）某品牌雪糕（如图），5支装一盒，8盒装一箱。妈妈买了一箱，共重( )千克。需要支付( )元。
3．（2分）四（1）班共30人，这学期每人新买了一套校服，其中上衣每件55元，裤子每条45元，全班买校服一共花了( )元。
4．（2分）在口里填入相同的数，使等式34×口＋56×口＝810成立，口里应填( )。
5．（2分）淘气使用计算器计算时，数字按键“6”不灵了，他可以转化成( )也能计算出结果。
6．（2分）在计算25×44时可以运用( )律将算式写成25×40＋25×4；也可以运用乘法结合律将算式写成( )进行简算。
7．（2分）塔云山位居镇安县城西约20千米处，是秦岭山系中一颗璀璨的明珠。塔云山游客中心5月共购进了25箱消毒液，每箱装11盒，每盒装4瓶。塔云山游客中心5月共购进了( )瓶消毒液。
8．（2分）小马虎把12×（A＋4）错算成12×A＋4，计算结果与正确答案相差( )。
9．（2分）聪聪在解决一道三位数乘两位数的乘法算式时，在纸上写了156×6＋156×40，他可能在解决算式( )，我是这样想的：( )。
10．（2分）74－（34－19）＝74－34＋19，观察这个等号左右两边算式的相同点和不同点，仿照算式，再写出一个这样的算式：( )。
二、判断题（共10分）
11．48×99＝48×（100－1）＝4800－1＝4799。( )
12．计算25×44时，聪聪用的方法是：25×44＝25×（4×11）＝25×4×11。他应用的是乘法结合律。( )
13．29＋22＋78＝29＋100。( )
14．64×64＋36×64＝（64＋36）×64。( )
15．52＋83＋48＝83＋（52＋48）这一步计算只运用了加法结合律。( )
三、选择题（共10分）
16．（2分）小明在计算87×25时，不小心看成了89×25，他只要用得到的结果再减去（ ）就能得到原来正确的数。
A．2×25 B．2×87 C．2×89 D．12×25
17．（2分）以下四个运算的式子中：①（3＋4）＋5＝3＋（4＋5）；②（3－4）－5＝3－（4－5）；③（3÷4）÷5＝3÷（4÷5）；④（3×4）×5＝3×（4×5）。正确的运算式子有（ ）个。
A．1 B．2 C．3 D．4
18．（2分）下图中，能说明“”与“”相等的是（ ）。
A．①② B．②③ C．②④ D．③④
19．（2分）与65×99相等的算式是（ ）。
A．65×100－1 B．65×100＋65 C．65×100－65 D．60×99＋5
20．（2分）根据商的变化规律，计算360÷24做法不正确的是（ ）。
A．（360×2）÷（24×2） B．（360÷6）÷（24÷6）
C．360÷6×4 D．360÷6÷4
四、计算题（共6分）
21．（6分）怎样简便就怎样计算。
1600÷25÷4 528－167－128 16×23－6×23
38＋38×99 230＋165＋35 48×101
五、解答题（共54分）
22．（6分）东方服装厂一套小学生秋装85元，一套夏装65元，实验小学四年二班有40人，每人预定了一套秋装和夏装，一共要花多少元？
23．（6分）明珠小学401班共有学生43人，在运动会开幕式上要进行集体武术操表演，学校为他们购买了演出服。其中上衣每件42元，裤子每条58元。学校共花了多少元为401班购买演出服？
24．（6分）欢欢坚持每天练字，3个星期共写了4200个钢笔字，欢欢平均每天写多少个钢笔字？（一星期按7天计算）
25．（6分）2022年6月2日国务院联防联控机制召开发布会：全国疫情呈现稳定下降态势，但要警惕疫情反弹风险，要求主动做好个人防护，佩戴口罩。知音社区新运回7箱口罩，每箱装有40袋，每袋25个口罩，知音社区新运回口罩多少个？
26．（6分）扶贫助农在行动，桃园村的水果丰收了，受疫情影响销售困难，各地超市纷纷伸出援手进行订购。胜利超市订购了25车水果，每辆车装14箱水果，每箱水果重20千克，胜利超市一共订购了水果多少千克？
27．（6分）小强看一本345页的童话书，第一天看了43页，第二天看了57页，第三天看了45页。还剩多少页没看？（用两种方法）
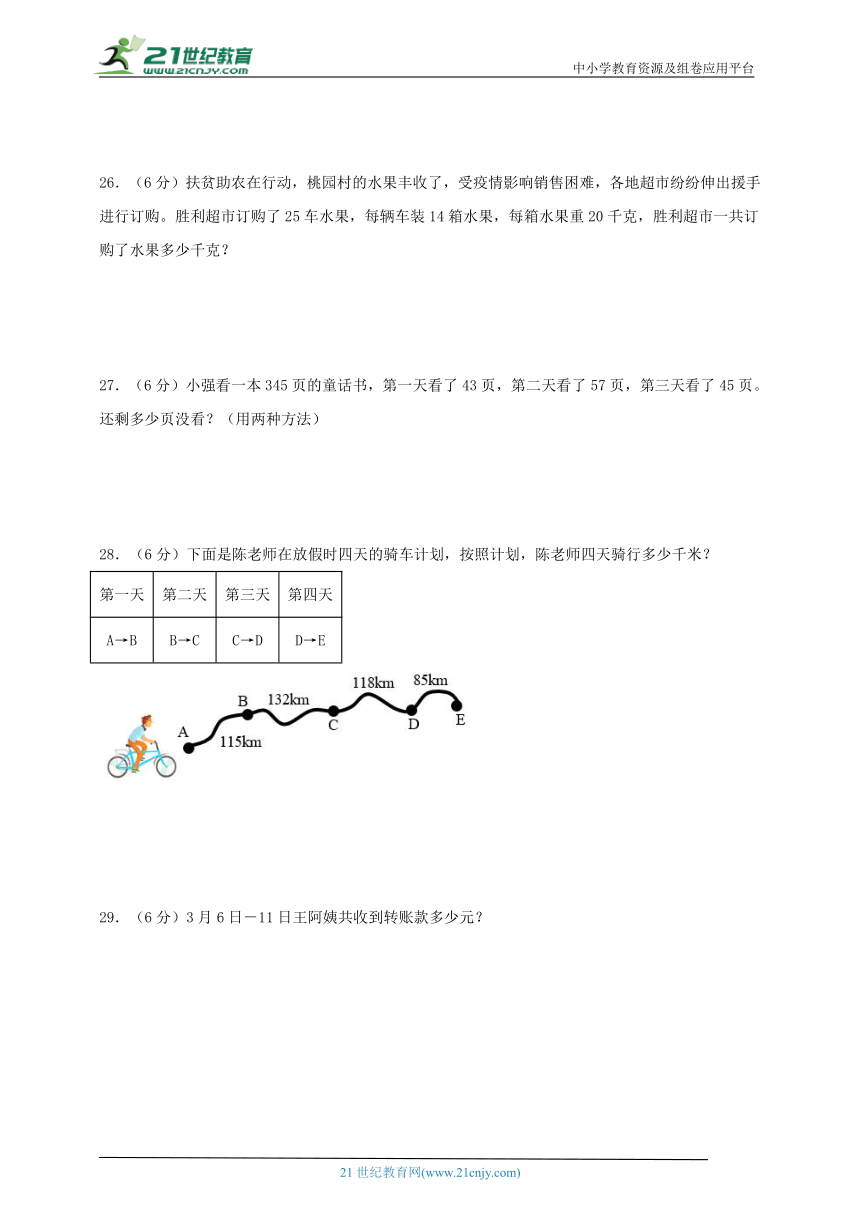
28．（6分）下面是陈老师在放假时四天的骑车计划，按照计划，陈老师四天骑行多少千米？
第一天 第二天 第三天 第四天
A→B B→C C→D D→E
29．（6分）3月6日－11日王阿姨共收到转账款多少元？
30．（6分）四年级（3）班举行趣味运动会，接力赛跑有A、B两组同学，每组选三名队员，A组三名队员分别跑100米、200米、300米，B组三名队员分别跑300米、200米、100米。这样比赛公平吗？为什么？
参考答案
1．乘法分配 58×32
＝58×（30＋2）
＝58×30＋58×2
＝1740＋116
＝1856
【分析】乘法分配律是指两个数的和同一个数相乘，等于把两个加数分别同这个数相乘，再把两个积加起来，结果不变，本题是把58看成（8＋50），再根据乘法分配律进行计算。
【详解】在这个竖式计算过程中运用了乘法分配律，用横式表示下边的竖式是
58×32
＝58×（30＋2）
＝58×30＋58×2
＝1740＋116
＝1856
【点睛】此题主要考查了学生对乘法分配律灵活掌握及运用。
2．5 160
【分析】根据题意，用125克乘上5求出一盒的质量，然后再乘上8，求出一箱的质量，再化成千克数；用4元乘上5求出一盒的钱数，然后再乘上8即可。
【详解】125×5×8
＝125×8×5
＝1000×5
＝5000（克）
5000克＝5千克
4×5×8
＝20×8
＝160（元）
【点睛】考查了运用整数乘法的意义解决实际问题的能力。
3．3000
【分析】根据题意，回想单价、数量和总价之间的关系，单价×数量＝总价；先求出一套校服的单价，用55加45即可；再用一套校服的单价乘四（1）班的总人数就是全班买校服一共需要花的钱数。
【详解】（55＋45）×30
＝100×30
＝3000（元）
全班买校服一共花了3000元。
【点睛】解决此题应根据总价、数量和单价三者之间的关系进行解答，同时也考查了乘法分配律运算定律在计算过程中的灵活运用。
4．9
【分析】乘法分配律是指两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加；据此解题即可。
【详解】34×口＋56×口
＝（34＋56）×口
＝90×□
＝810
810÷90＝9
可得：在口里填入相同的数，使等式34×口＋56×口＝810成立，口里应填9。
【点睛】正确理解乘法分配律的意义，是解答此题的关键。
5．25×4×4
【分析】把16看成4×4，再按照乘法结合律计算，把25×16转化成25×4×4（答案不唯一）。
【详解】淘气使用计算器计算时，数字按键“6”不灵了，他可以转化成（25×4×4）也能计算出结果。
【点睛】此题也可把25×16转化成25×2×8。
6．乘法分配 25×4×11
【分析】（1）乘法分配律是指两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。
（2）乘法结合律：三个数相乘，先把前两个数相乘，再和另外一个数相乘，或先把后两个数相乘，再和另外一个数相乘，积不变。
【详解】25×44
＝25×（40＋4）
＝25×40＋25×4
＝1000＋100
＝1100
25×44
＝25×4×11
＝100×11
＝1100
所以，在计算25×44时可以运用乘法分配律将算式写成25×40＋25×4；也可以运用乘法结合律将算式写成25×4×11进行简算。
【点睛】正确理解乘法结合律和乘法分配律的意义，是解答此题的关键。
7．1100
【分析】用每盒装的瓶数乘盒数，求出每箱有多少瓶，再乘箱数，即可求出塔云山游客中心5月共购进了多少瓶消毒液。计算时，利用乘法交换律可以简算。
【详解】4×11×25
＝4×25×11
＝100×11
＝1100（瓶）
所以，塔云山游客中心5月共购进了1100瓶消毒液。
【点睛】本题主要考查了两位数乘两位数乘法的计算，也可以先求出25箱一共有多少盒，再乘每盒的瓶数，列式为：25×11×4。
8．44
【分析】首先根据乘法分配律，可得12×（A＋4）＝12×A＋12×4，然后再减去12×A＋4，求出他的计算结果与正确结果相差多少即可。
【详解】12×（A＋4）－（12×A＋4）
＝12A＋12×4－12A－4
＝12A－12A＋48－4
＝44
小马虎把12×（A＋4）错算成12×A＋4，计算结果与正确答案相差44。
【点睛】此题考查的目的是理解掌握乘法分配律的意义，并且能够灵活运用乘法分配律进行简便计算。
9．156×46 见详解
【分析】156×6＋156×40表示6个156与40个156的和是多少，即共有46个156即为156与46的积，依据为乘法分配律。
【详解】156×6＋156×40
＝156×（6＋40）
＝156×46
他可能在解决算式156×46，我是这样想的：156×6＋156×40＝156×（6＋40）＝156×46。
【点睛】考查学生对乘法分配律的应用情况。
10．126－（26－9）＝126－26＋9
【分析】整数减法的性质：一个数连续减去两个数，可以用这个数减去两个数的和；用字母表示为：a－b－c＝a－（b＋c）；据此解答即可。
【详解】74－（34－19）
＝74－34＋19
＝40＋19
＝59
74－（34－19）＝74－34＋19，观察这个等号左右两边算式的相同点和不同点，仿照算式，再写出一个这样的算式：126－（26－9）＝126－26＋9。（答案不唯一）
【点睛】本题考查了整数减法的性质的灵活运用。
11．×
【分析】把99看成是100与1的差，再根据乘法分配律计算。
【详解】48×99
＝48×（100－1）
＝48×100－48
＝4800－48
＝4752
所以原题计算错误。
故答案为：×。
【点睛】乘法分配律是指两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。正确理解乘法分配律的意义，并会灵活运用，是解答此题的关键。
12．√
【分析】计算25×44时，把44分解成4×11，这样变成三个数相乘，把先乘后两个数变成了先乘前两个数，即运用乘法结合律进行简算。
【详解】25×44
＝25×（4×11）
＝25×4×11（乘法结合律）
＝100×11
＝1100
这是运用了乘法结合律简算，原题说法正确。
故答案为：√
【点睛】乘法结合律：先乘前两个数，或先乘后两个数，积不变，如a×b×c＝a×（b×c）。
13．√
【分析】三个数相加，先把前两个数相加，或者先把后两个数相加，和不变，这叫加法结合律。据此解答。
【详解】29＋22＋78
＝29＋（22＋78）
＝29＋100
＝129
由上述计算过程可知，29＋22＋78＝29＋100。题目说法正确。
故答案为：√
14．√
【分析】根据乘法分配律a×（b＋c）＝a×b＋a×c，a＝64，b＝64，c＝36，即可得解。
【详解】根据分析可知：64×64＋36×64＝（64＋36）×64。原题表述正确。
故答案为：√
15．×
【分析】加法交换律的概念：两个数相加，交换两个加数的位置，和不变；加法结合律的概念：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。据此判断即可。
【详解】52＋83＋48
＝83＋52＋48 （此步运用了加法交换律）
＝83＋（52＋48） （此步运用了加法结合律）
所以，此运算运用了加法交换律和加法结合律。
故答案为：×
16．A
【分析】把87×25看成89×25，相当于多计算了（89－87）个25，据此即可解答。
【详解】89×25－87×25
＝（89－87）×25
＝2×25
故答案为：A
【点睛】此题主要考查了乘法分配律的灵活运用。
17．B
【分析】根据整数混合运算的运算法则对每个算式进行排除，即可得解。
【详解】①根据加法的结合律可知，（3＋4）＋5＝3＋（4＋5），故①正确；
②（3－4）－5为减法运算，将括号去掉即为3－4－5，若将后面两个数字加上括号为3－（4＋5）≠3－（4－5），故②错误；
③（3÷4）÷5为除法运算，去掉括号为3÷4÷5，应等于3÷（4×5），不等于3÷（4÷5），③错误；
④根据乘法的结合律，（3×4）×5＝3×（4×5），故④正确；
正确的有两个，故答案为：B。
【点睛】本题考查整数混合运算的基本法则，学生只要掌握好运算方法即可。
18．B
【分析】①看图可知，整条线段共3段，将三段长度相加等于整条线段长度。
②长方形的面积＝长×宽，分别求出两个小长方形的面积相加，是整个图形的面积；整个图形是个长方形，也可以先求出大长方形的长，再根据长方形面积公式计算。
③总个数＝黑色圆形个数＋白色圆形个数，用每行个数×行数，可以分别求出黑色圆形个数和白色圆形个数；也可以不管颜色，直接用整体的每行个数×行数，求出总个数。
④单价×数量＝总价，总钱数＝本子单价×本数＋笔的单价×支数；因为本子和笔的数量不同，没法先求出本子和笔的单价和，再进而求出总钱数。
【详解】①6＋4＋3＝13（厘米）
不能说明“”与“”相等。
②6×3＋4×3
＝18＋12
＝30（cm2）
（6＋4）×3
＝10×3
＝30（cm2）
能说明“”与“”相等。
③6×3＋4×3
＝18＋12
＝30（个）
（6＋4）×3
＝10×3
＝30（个）
能说明“”与“”相等。
④6×3＋4×4
＝18＋16
＝34（元）
不能说明“”与“”相等。
能说明“”与“”相等的是②③。
故答案为：B
19．C
【分析】（1）99可以改写成100－1，再利用乘法的分配律，算式化为65×100－65，所以65×99与65×100－1的结果不相等；
（2）99可以改写成100－1，再利用乘法的分配律，算式化为65×100－65，所以65×99与65×100＋65的结果不相等；
（3）99可以改写成100－1，再利用乘法的分配律，算式化为65×100－65，所以65×99与65×100－65的结果相等；
（4）65可以改写成60＋5，再利用乘法的分配律，算式化为60×99＋5×99，所以65×99与60×99＋5的结果不相等；
【详解】A．65×99＝65×（100－1）＝65×100－65×1＝65×100－65，所以65×99与65×100－1的结果不相等；
B．65×99＝65×（100－1）＝65×100－65×1＝65×100－65，所以65×99与65×100＋65的结果不相等；
C．65×99＝65×（100－1）＝65×100－65×1＝65×100－65，所以65×99与65×100－65的结果相等；
D．65×99＝（60＋5）×99＝60×99＋5×99，所以65×99与60×99＋5的结果不相等；
故答案为：C
20．C
【分析】商不变的规律：被除数和除数都乘或除以一个相同的数（0除外），商不变；
在除法算式里，一个数连续除以两个数，等于用这个数除以这两个数的积；据此解答即可。
【详解】360÷24＝15
A．（360×2）÷（24×2）＝720÷48＝15，被除数和除数都同时乘2，商不变，故原题做法正确；
B．（360÷6）÷（24÷6）＝60÷4＝15，被除数和除数都同时除以6，商不变，故原题做法正确；
C．360÷6×4≠360÷24，故原题做法不正确；
D．360÷6÷4＝360÷（6×4）＝360÷24＝15，连续除以两个数等于除以这两个数的积，故原题做法正确。
故答案为：C
21．16；233；230
3800；430；4848
【分析】（1）根据除法的性质，先计算25×4，再用1600除以这个积。
（2）根据减法的性质，先计算528－128，再用差减167。
（3）根据乘法分配律，先计算16－6，再用差乘23。
（4）根据乘法分配律，先计算1＋99，再用和乘38。
（5）根据加法结合律，先计算165＋35，再用230加这个和。
（6）将101看成100＋1，根据乘法分配律，用48分别乘100和1，再将两个积相加。
【详解】1600÷25÷4
＝1600÷（25×4）
＝1600÷100
＝16
528－167－128
＝528－128－167
＝400－167
＝233
16×23－6×23
＝（16－6）×23
＝10×23
＝230
38＋38×99
＝38×（1＋99）
＝38×100
＝3800
230＋165＋35
＝230＋（165＋35）
＝230＋200
＝430
48×101
＝48×（100＋1）
＝48×100＋48×1
＝4800＋48
＝4848
22．6000元
【分析】根据题意可知，每套秋装的价钱×秋装的套数＋每套夏装的价钱×夏装的套数＝买这些衣服需要的钱，依此列式，由于秋装需要40套，夏装需要40套，因此可根据乘法分配律的特点进行简算。
【详解】85×40＋65×40
＝（85＋65）×40
＝150×40
＝6000（元）
答：一共要花6000元。
【点睛】此题考查的是经济问题的计算，运用乘法分配律的特点进行计算更加简便。
23．4300元
【分析】先计算出每一套衣服需要多少钱，再用每套衣服的价钱乘购买的套数，即可算出一共需要多少钱。据此解答。
【详解】（42＋58）×43
＝100×43
＝4300（元）
答：学校共花了4300元为401班购买演出服。
【点睛】本题主要考查混合运算，也可以用上衣的单价×数量＋裤子的单价×数量进行求解。
24．200个
【分析】根据题意可知，3个星期共写钢笔字的数量÷3＝1个星期共写钢笔字的数量，1个星期共写钢笔字的数量÷7＝欢欢平均每天写钢笔字的数量，即3个星期共写钢笔字的数量÷3÷7＝欢欢平均每天写钢笔字的数量，依此列出综合算式，并根据整数除法的性质进行计算即可。
【详解】4200÷3÷7
＝4200÷（3×7）
＝4200÷21
＝200（个）
答：欢欢平均每天写200个钢笔字。
【点睛】此题考查的是工程问题的计算，运用整数除法的性质进行计算更加简便。
25．7000个
【分析】每袋口罩的个数乘每箱的袋数，再乘运回的箱数即可解答。
【详解】25×40×7
＝1000×7
＝7000（个）
答：知音社区新运回口罩7000个。
【点睛】本题主要考查学生对乘法结合律的掌握和灵活运用。
26．7000千克
【分析】用每箱水果的质量乘14，可以计算出每车水果的质量，再用每车水果的质量乘25，计算出胜利超市一共订购了水果多少千克即可。
【详解】20×14×25
＝20×25×14
＝500×14
＝7000（千克）
答：胜利超市一共订购了水果7000千克。
【点睛】本题解题关键是先用乘法计算出每车水果的质量。
27．200页
【分析】方法一：43加57，再加45等于三天看了的页数和，用345减三天看了的页数和等于还剩下没看的页数；方法二：用345连续减43、57、45即可解答。
【详解】方法一：
345－（43＋57＋45）
＝345－145
＝200（页）
答：还剩200页没看。
方法二：
345－43－57－45
＝302－57－45
＝245－45
＝200（页）
答：还剩200页没看。
【点睛】本题可以先求看了的页数和，再求剩下页数；也可以用童话书的页数连续减去三天看了的页数求解。
28．450千米
【分析】计算陈老师四天骑行的总路程，用加法计算，依此列式并根据加法交换律和加法结合律的特点进行简算即可。
【详解】115＋132＋118＋85
＝（115＋85）＋（132＋118）
＝200＋250
＝450（千米）
答：按照计划，陈老师四天骑行450千米。
【点睛】此题考查的是根据加法交换律和加法结合律的特点解决实际问题，应熟练掌握。
29．728元
【分析】根据题意，用来自陈明的转账加上来自李林的转账，再加上来自张丽的转账，即可得到3月6日－11日王阿姨共收到转账款多少元，据此解答。
【详解】
（元）
30．公平；因为每组跑的总长度是一样的
【分析】分别将每组三名队员跑步路程相加，求出每组跑步总路程，根据加法交换律进行判断即可。
【详解】100＋200＋300＝300＋200＋100＝600（米）
答：公平，因为每组跑的总长度是一样的。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑