资源简介

中小学教育资源及组卷应用平台
第九章平面直角坐标系期中复习人教版2024—2025学年七年级下册
一、选择题
1．若xy＞0，则关于点P（x，y）的说法正确的是（　　）
A．在一或二象限 B．在一或四象限
C．在二或四象限 D．在一或三象限
2．下列描述中，能确定位置的是（　　）
A．济南市泉城路
B．电影院1号厅2排
C．北纬36.7°，东经117.0°
D．南偏西40°
3．点P在第二象限内，点P到x轴的距离是6，到y轴的距离是2，那么点P的坐标为（　　）
A．（﹣6，2） B．（﹣2，﹣6） C．（﹣2，6） D．（2，﹣6）
4．在平面直角坐标系中，若点A先向右平移4个单位，再向上平移6个单位后得到点B（2，4），则点A的坐标是（　　）
A．（8，8） B．（6，10） C．（﹣4，0） D．（﹣2，﹣2）
5．点P（t+3，t+2）在直角坐标系的x轴上，则P点坐标为（　　）
A．（0，﹣2） B．（﹣2，0） C．（1，2） D．（1，0）
6．在平面直角坐标系中，点A的坐标为（﹣7，3），点B的坐标为（3，3），则线段AB的位置特征为（　　）
A．与x轴平行
B．与y轴平行
C．在第一、三象限的角平分线上
D．在第二、四象限的角平分线上
7．已知点A（3a+5，a﹣3）在第一、三象限的角平分线上，则a的值为（　　）
A．﹣5 B．﹣4 C．﹣3 D．﹣2
8．已知点Q的坐标为（﹣2+a，2a﹣7），且点Q到两坐标轴的距离相等，则点Q的坐标是（　　）
A．（3，3） B．（3，﹣3）
C．（1，﹣1） D．（3，3）或（1，﹣1）
9．如图，在正方形网格中，若点A（1，1），点C（3，﹣2），则点B的坐标为（　　）
（1，2） B．（0，2）
C．（2，0） D．（2，1）
10．点P坐标为（m+1，m﹣2），则点P不可能在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
二、填空题
11．已知点P（2m+4，m﹣1）在第一象限，到x轴的距离为2，则m＝　　．
12．已知点M（3，1），N（a，a+3），若直线MN与y轴平行，则线段MN的长为 　 　．
13．若点P（m，1﹣2m）在第二、四象限的角平分线上，则m的值为 　 　．
14．在平面直角坐标系中，点A（﹣2，0），B（0，3），将线段AB平移后，得到线段CD，点A与点C对应，若点C（2，a），点D（b，0），则a+b＝　 　．
15．已知点P（a，b）到x轴的距离是2，到y轴的距离是5，且|a﹣b|＝a﹣b，则P点坐标是　 　．
16．如图，动点P从坐标原点（0，0）出发，以每秒一个单位长度的速度按图中箭头所示的方向运动，第1秒运动到点（1，0），第2秒运动到（1，1），第3秒运动到（0，1），第4秒运动到点（0，2），…则第9秒点P所在位置的坐标是　 　，第2024秒点P所在位置的坐标是　 　．
三、解答题
17．在平面直角坐标系中，已知点M（m﹣2，2m﹣7），点N（n，3）．
（1）若M在x轴上，求M点的坐标；
（2）若MN∥y轴，且MN＝2，求n的值．
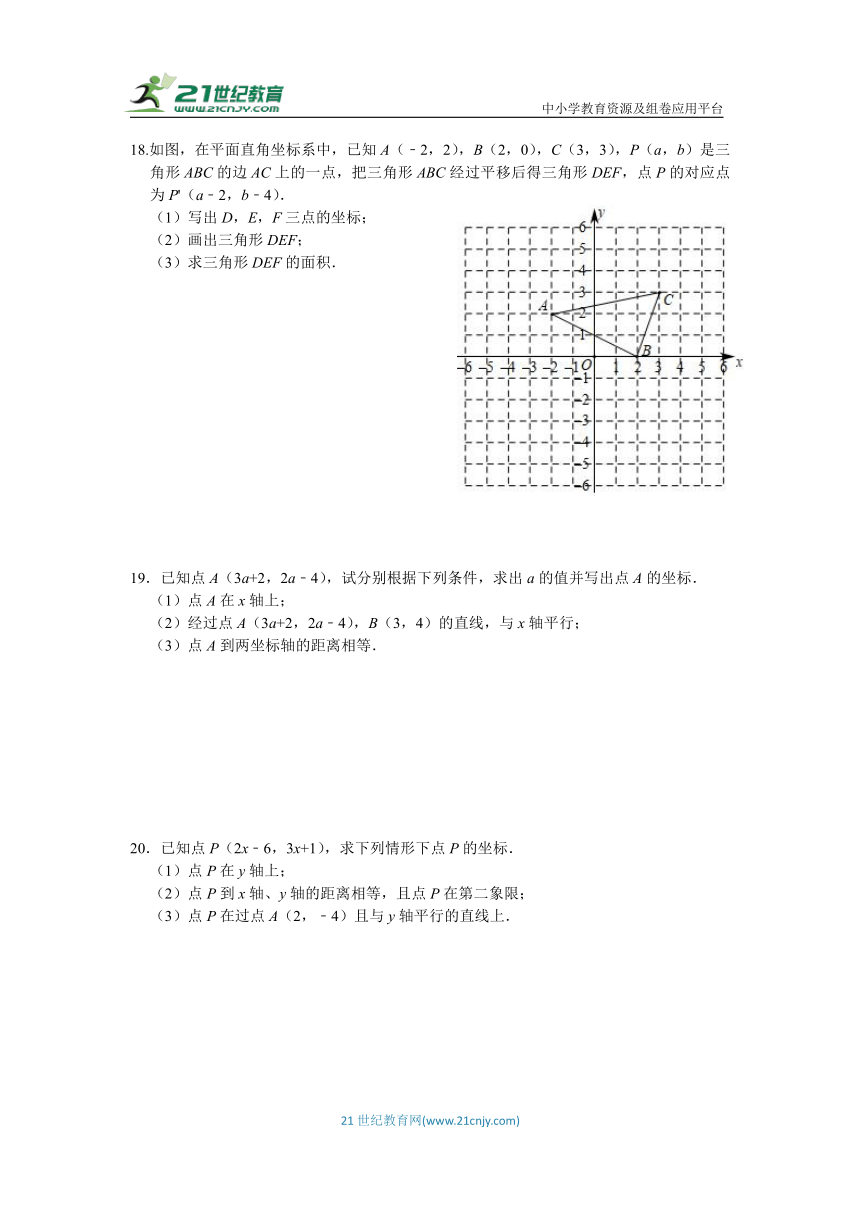
18.如图，在平面直角坐标系中，已知A（﹣2，2），B（2，0），C（3，3），P（a，b）是三角形ABC的边AC上的一点，把三角形ABC经过平移后得三角形DEF，点P的对应点为P'（a﹣2，b﹣4）．
（1）写出D，E，F三点的坐标；
（2）画出三角形DEF；
（3）求三角形DEF的面积．
19．已知点A（3a+2，2a﹣4），试分别根据下列条件，求出a的值并写出点A的坐标．
（1）点A在x轴上；
（2）经过点A（3a+2，2a﹣4），B（3，4）的直线，与x轴平行；
（3）点A到两坐标轴的距离相等．
20．已知点P（2x﹣6，3x+1），求下列情形下点P的坐标．
（1）点P在y轴上；
（2）点P到x轴、y轴的距离相等，且点P在第二象限；
（3）点P在过点A（2，﹣4）且与y轴平行的直线上．
21．已知：A（0，1），B（2，0），C（4，3）
（1）在坐标系中描出各点，画出△ABC．
（2）求△ABC的面积；
（3）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．
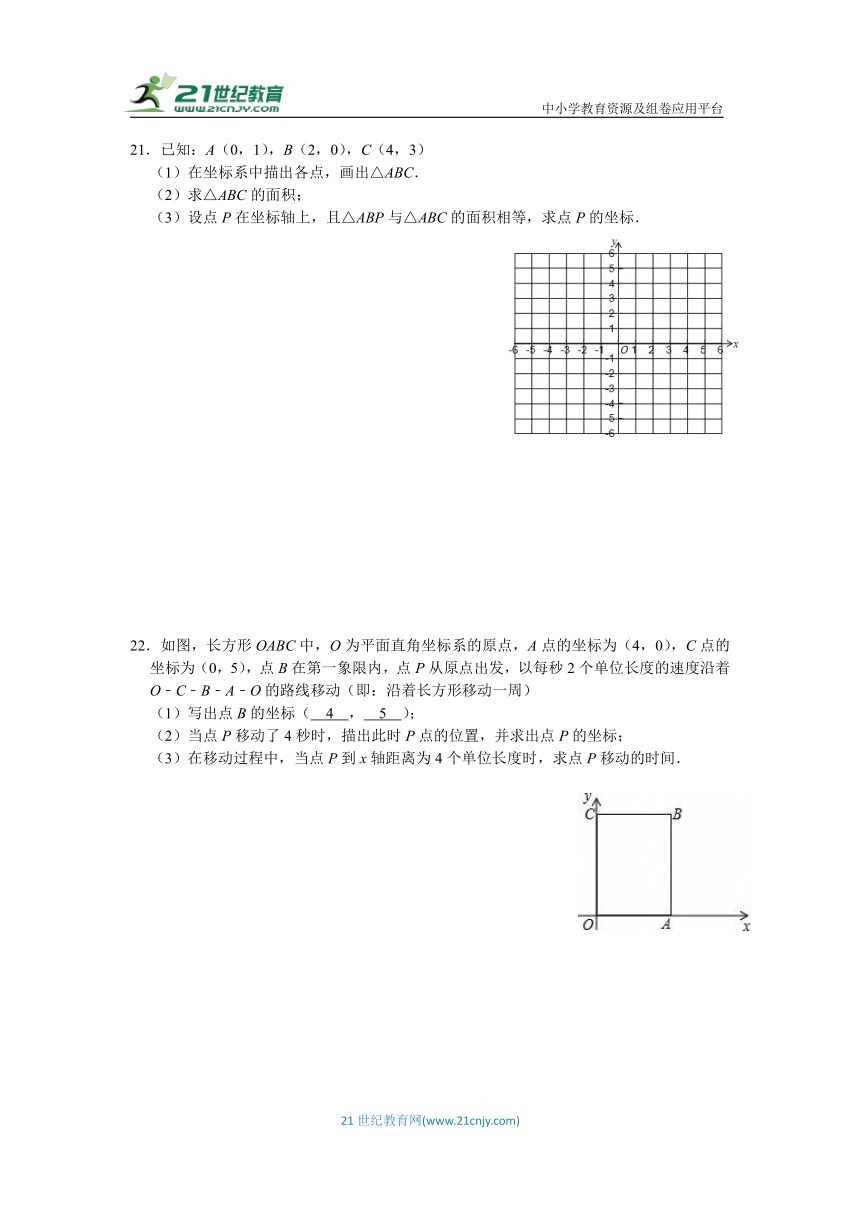
22．如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，5），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动（即：沿着长方形移动一周）
（1）写出点B的坐标（　4　，　5　）；
（2）当点P移动了4秒时，描出此时P点的位置，并求出点P的坐标；
（3）在移动过程中，当点P到x轴距离为4个单位长度时，求点P移动的时间．
参考答案
一、选择题
1．【解答】解：∵xy＞0，
∴x＞0，y＞0或x＜0，y＜0，
∴点P（x，y）在一或三象限．
故选：D．
2．电影院1号厅2排，不知道是第二排的第几个座位，不能确定具体位置，故选项B不符合题意；
北纬36.7°，东经117.0°，可以确定具体的位置，故选项C符合题意；
南偏西40°，不能确定具体位置，故选项D不符合题意，
故选：C．
3．【解答】解：∵点P在第二象限内，点P到x轴的距离是6，到y轴的距离是2，
∴点P的横坐标为﹣2，纵坐标为6，
∴点P的坐标为（﹣2，6）．
故选：C．
4．【解答】解：将若点A先向右平移4个单位，再向上平移6个单位后得到点B（2，4），
则点A的坐标为（2﹣4，4﹣6），即（﹣2，﹣2），
故选：D．
5．【解答】解：∵点P（t+3，t+2）在直角坐标系的x轴上，
∴t+2＝0，
解得：t＝﹣2，
故t+3＝1，
则P点坐标为（1，0）．
故选：D．
6．【解答】解：选：A．
7．【解答】解：点A（3a+5，a﹣3）在第一、三象限的角平分线上，且第一、三象限角平分线上的点的坐标特点为：点的横纵坐标相等，
∴3a+5＝a﹣3，
解得a＝﹣4．
故选：B．
8．【解答】解：∵点Q（﹣2+a，2a﹣7）到两坐标轴的距离相等，
∴|﹣2+a|＝|2a﹣7|，
∴﹣2+a＝2a﹣7或﹣2+a＝﹣（2a﹣7），
解得a＝5或a＝3，
所以，点Q的坐标为（3，3）或（1，﹣1）．
故选：D．
9．【解答】解：如图所示：点B的坐标为（2，0）．
故选：C．
10．【解答】解：当m＞2时，m﹣2＞0，故点P可能在第一象限，故选项A不合题意；
当﹣1＜m＜2时，m+1＞0，m﹣2＜0，故点P可能在第四象限，故选项D不合题意；
当m＜﹣1时，m+1＜0，m﹣2＜0，故点P可能在第三象限，故选项C不合题意；
因为m+1＞m﹣2，所以无论m取何值，点P不可能在第二象限，故选项B符合题意；
故选：B．
二、填空题
11．【解答】解：∵点P（2m+4，m﹣1）在第一象限，且到x轴的距离是2，
∴m﹣1＝2，
解得：m＝3，
故答案为：3．
12．【解答】解：根据题意可知，直线MN与y轴平行，
∴a＝3，
则a+3＝6，
N（3，6），
又∵点M（3，1），
∴线段MN的长为6﹣1＝5，
故答案为：5．
13．【解答】解：∵点P（m，1﹣2m）在第二、四象限的角平分线上，
∴m+1﹣2m＝0，
解得：m＝1，
故答案为：1．
14．【解答】解：∵点A（﹣2，0）对应点C的坐标为C（2，a），点B（0，3）对应点D（b，0），
∴线段AB向右平移4个单位，向下平移3个单位得到线段CD，
∴a＝0﹣3＝﹣3，b＝0+4＝4，
∴a+b＝﹣3+4＝1，
故答案为：1．
15．【解答】解：∵丨a﹣b丨＝a﹣b，
∴a﹣b＝a﹣b或a﹣b＝﹣a+b，
∵P（a，b）到x轴的距离是2，到y轴的距离是5，
∴a≠b，
∴a﹣b≠﹣a+b，
∴a＝5，b＝±2，
∴P点的坐标为（5，2）或（5，﹣2），
故答案为：（5，2）或（5，﹣2）．
16．【解答】解：根据题意列出P的坐标寻找规律．
P1（1，0）；
P8（2，0）；
P24（4，0）；
P48（6，0）；
即P2n（2n+2）坐标为（2n，0）．
P2024（44，0）．
∴P2024坐标为P2024（44，0）故答案为：（2，1），（44，0）．
三、解答题
17．【解答】解：（1）∵M在x轴上，
∴2m﹣7＝0，
∴，
∴，
∴；
（2）∵MN∥y轴，
∴m﹣2＝n，
∵MN＝2，
∴|2m﹣7﹣3|＝2，
∴2m﹣10＝2或2m﹣10＝﹣2，
∴m＝6或4，
当m＝6时，n＝6﹣2＝4；
当m＝4时，n＝4﹣2＝2，
∴n＝4或2．
18.【解答】解：（1）D（﹣4，﹣2），E（0，﹣4），F（1，﹣1）；
（2）如图所示：△DEF即为所求；
（3）S△DEF＝5×3﹣×5×1﹣×4×2﹣×1×3
＝15﹣2.5﹣4﹣1.5
＝7．
19．【解答】解：（1）依题意有2a﹣4＝0，
解得a＝2，
3a+2＝3×2+2＝8．
故点A的坐标为（8，0）；
（2）依题意有2a﹣4＝4，
解得a＝4，
3a+2＝3×4+2＝14，
故点A的坐标为（14，4）；
（3）依题意有|3a+2|＝|2a﹣4|，
则3a+2＝2a﹣4或3a+2+2a﹣4＝0，
解得a＝﹣6或a＝0.4，
当a＝﹣6时，3a+2＝3×（﹣6）+2＝﹣16，
当a＝0.4时，3a+2＝3×0.4+2＝3.2，2a﹣4＝﹣3.2．
故点A的坐标为（﹣16，﹣16）或（3.2，﹣3.2）．
20．【解答】解：（1）∵点P（2x﹣6，3x+1），且点P在y轴上，
∴2x﹣6＝0，
∴x＝3，
∴3x+1＝10，
∴点P的坐标为（0，10）；
（2）∵点P（2x﹣6，3x+1），点P到x轴、y轴的距离相等，且点P在第二象限，
∴2x﹣6＝﹣（3x+1），
∴2x﹣6+3x+1＝0，
∴x＝1，
∴2x﹣6＝﹣4，3x+1＝4，
∴点P的坐标为（﹣4，4）；
（3）∵点P（2x﹣6，3x+1）在过点A（2，﹣4）且与y轴平行的直线上，
∴2x﹣6＝2，
∴x＝4，
∴3x+1＝13，
∴点P的坐标为（2，13）．
21．【解答】解：（1）如图所示：
（2）过点C向x、y轴作垂线，垂足为D、E．
∴四边形DOEC的面积＝3×4＝12，△BCD的面积＝＝3，△ACE的面积＝＝4，△AOB的面积＝＝1．
∴△ABC的面积＝四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
＝12﹣3﹣4﹣1＝4．
（3）当点p在x轴上时，△ABP的面积＝＝4，即：，解得：BP＝8，
所点P的坐标为（10，0）或（﹣6，0）；
当点P在y轴上时，△ABP的面积＝＝4，即，解得：AP＝4．
所以点P的坐标为（0，5）或（0，﹣3）．
所以点P的坐标为（0，5）或（0，﹣3）或（10，0）或（﹣6，0）．
22．【解答】解：（1）点B的坐标（4，5），故答案为：4，5；
（2）当点P移动了4秒时，点P移动了4×2＝8个单位长度，
∵C点的坐标为（0，5），∴OC＝5，∴8﹣5＝3，
∴此时，点P的位置在线段BC上，且CP＝3，
如图所示，点P的坐标为BC边中点（3，5）．
（3）当点P在OC上时，OP＝4，
此时所用时间为4÷2＝2（s）；
当点P在AB上时，AP＝4，BP＝1，
∵A点的坐标为（4，0）∴OA＝CB＝4，
∵C点的坐标为（0，5）∴OC＝5，OC+CB+BP＝5+4+1＝10，此时所用时间为
10÷2＝5（s）；
综上所述，当点P移动2秒或5秒时，点P到x轴的距离为4个单位长度．
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑