资源简介

(共13张PPT)
人教版 数学 七年级 下册
7.2.2平行线的判定（1）
温故知新
除应用以上两种方法以外，是否还有其它方法呢？
温故知新
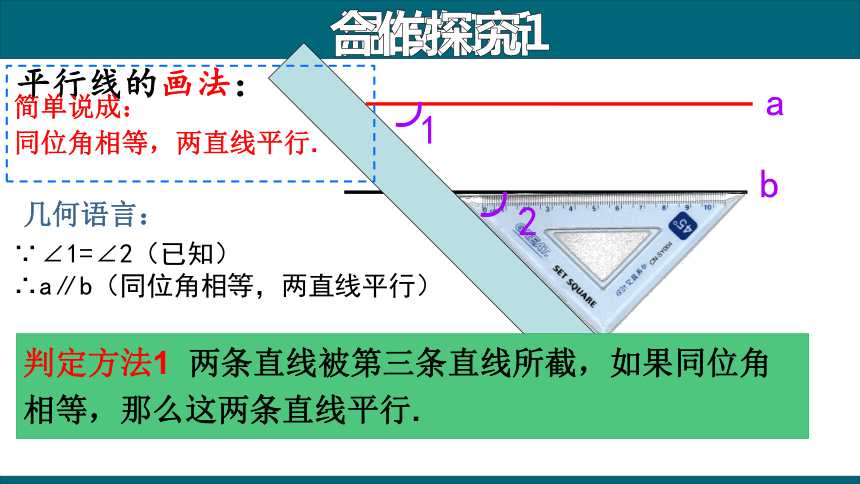
平行线的画法：
）
）
判定方法1 两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.
合作探究1
简单说成：
同位角相等，两直线平行.
1
2
a
b
几何语言：
∵∠1=∠2（已知）
∴a∥b（同位角相等，两直线平行）
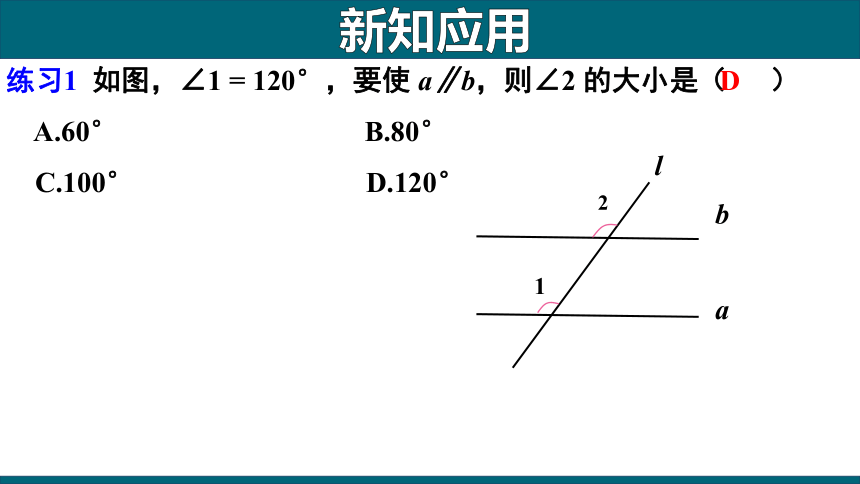
练习1 如图，∠1 = 120°，要使 a∥b，则∠2 的大小是（ ）
A.60° B.80°
C.100° D.120°
a
b
l
1
2
D
新知应用
合作探究2
由同位角相等可以判定两直线平行，能否利用内错角来判定两直线平行呢？
如图，已知 3= 2，求证：a//b。
2
b
a
1
3
）
）
）
判定方法2 两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
简单说成：
内错角相等，两直线平行.
几何语言：
∵∠3=∠2（已知）
∴a∥b（内错角相等，两直线平行）
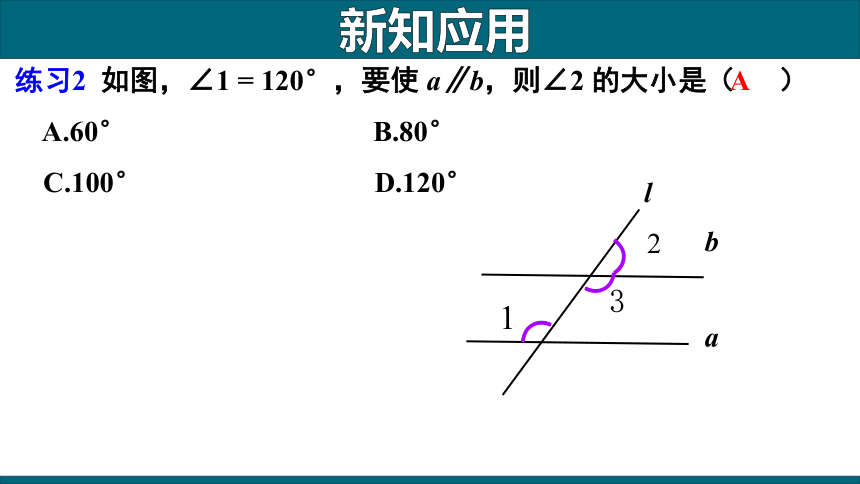
练习2 如图，∠1 = 120°，要使 a∥b，则∠2 的大小是（ ）
A.60° B.80°
C.100° D.120°
a
b
l
1
2
A
新知应用
）
）
）
3
合作探究3
如图，如果∠1+∠2＝180 ，你能判定AB∥CD吗
1
3
2
A
B
C
D
E
F
﹚
﹚
﹚
判定方法3 两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.
简单说成：
同旁内角互补，两直线平行.
几何语言：
∵∠1+∠2=180 （已知）
∴AB∥CD（同旁内角互补，两直线平行）
新知应用
练习3 如图，∠ACB=90°，∠A=35°，∠BCD=55°.试说明：AB∥CD.
课堂小结
文字简述 符号语言 图示
同位角相等， 两直线平行 因为________， 所以a∥b
内错角相等， 两直线平行 因为________， 所以a∥b 同旁内角互补，两直线平行 因为___________，所以a∥b ∠1=∠4
∠1=∠2
∠1+∠3=180°
a
b
c
3
1
2
4
感
谢
观
看
新知应用
① ∵ ∠1 =_____（已知）
∴ AB∥CE( )
② ∵ ∠1 +_____=180o（已知）
∴CD∥BF( )
③ ∵ ∠1 +∠5 =180o（已知）
∴ ___∥_____( )
AB
CE
∠2
④ ∵ ∠4 +_____=180o（已知）
∴ CE∥AB( )
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
4.根据条件完成填空.
∠3
新知应用
练习4如图所示，木工师傅在一块木板上画两条平行线，方法是：
用角尺画木板边缘的两条垂线，这样画的理由有下列4种说法：
其中正确的是( )
①同位角相等，两直线平行；
②内错角相等，两直线平行；
③同旁内角互补，两直线平行；
A. ①②③ B.①②
C. ②③ D.①③
新知应用
例：在同一平面内，如果两条直线都垂直于同一条直线， 那么两条直线平行吗？为什么？
1
2
a
b
c
1
3
4
已知：直线b⊥a，c⊥a .求证： b∥c
∵b⊥a，c⊥a( )
∴∠1＝∠2＝90 ( )
∴b∥c( )
同一平面内，垂直于同一条直线的两条直线相互平行

展开更多......

收起↑