资源简介

(共32张PPT)
（人教版）数学（2025）
七年级
下
第七章 相交线与平行线
7.1 相交线
7.1.1 两条直线相交
导入新课
在上一章中,我们认识了许多几何图形,并学习了一些基本的平面图形——直线、射线、线段和角.
思路一
我们是否可以将两根木条抽象成两条直线呢
这样的两条直线有什么样的关系呢 这样的关系又应该怎样去识别和判断呢
这节课我们来研究两条直线相交.
导入新课
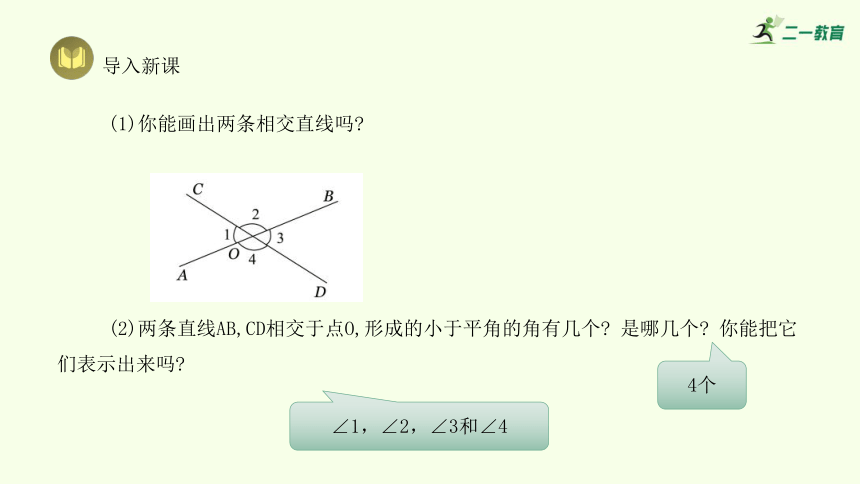
(1)你能画出两条相交直线吗
(2)两条直线AB,CD相交于点O,形成的小于平角的角有几个 是哪几个 你能把它们表示出来吗
4个
∠1，∠2，∠3和∠4
导入新课
在我们的生活中,蕴含着大量的相交线.菜园篱笆上交叉的竹竿,笔直的公路上的车行道线,大桥的吊索、钢梁上的钢条,棋盘中的横线和竖线,教室里课桌面、黑板面相邻的两条边与相对的两条……都给我们以相交线或平行线的形象.
直线相交可以形成哪些角 这些角又有什么特征
我们将通过研究直线相交所成的角的数量关系和位置关系研究相交线.
思路二
导入新课
你能否再举出一些相交线的例子
导入新课
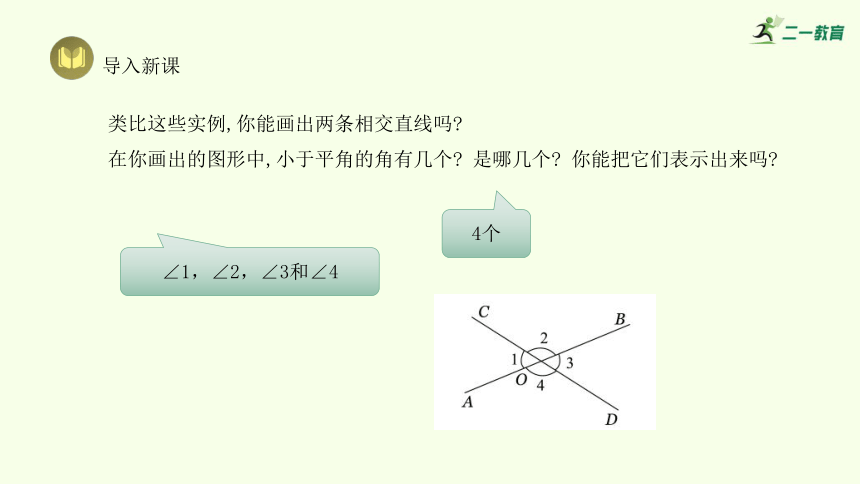
类比这些实例,你能画出两条相交直线吗
在你画出的图形中,小于平角的角有几个 是哪几个 你能把它们表示出来吗
4个
∠1，∠2，∠3和∠4
高效课堂
活动一:学生自主探究邻补角和对顶角
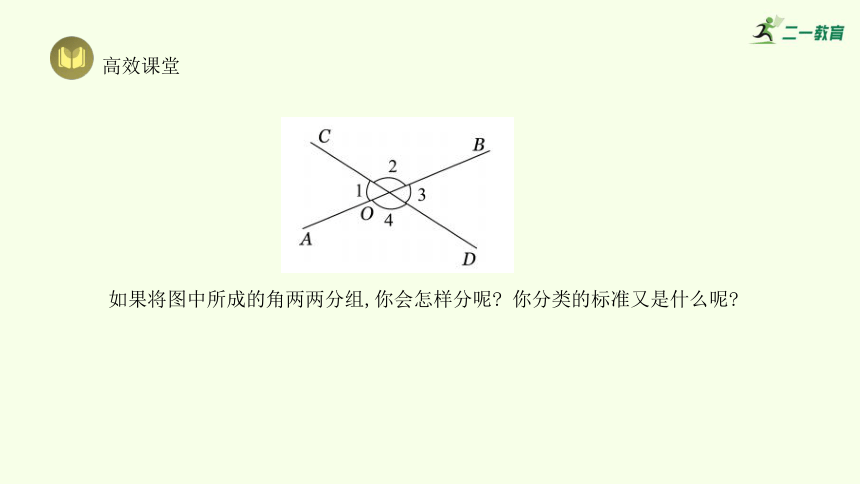
刚才同学们所画的两条相交直线各不相同,它们所成的角也在变化,你能发现这些角之间不变的关系吗
高效课堂
如果将图中所成的角两两分组,你会怎样分呢 你分类的标准又是什么呢
高效课堂
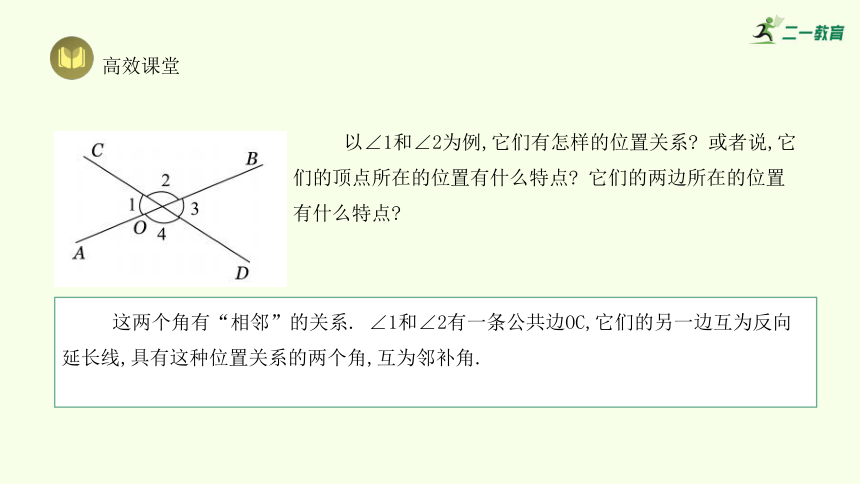
这两个角有“相邻”的关系. ∠1和∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种位置关系的两个角,互为邻补角.
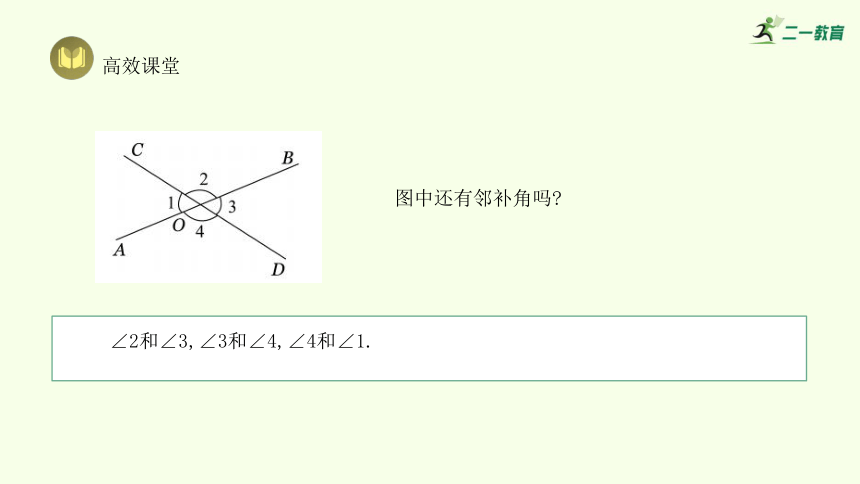
以∠1和∠2为例,它们有怎样的位置关系 或者说,它们的顶点所在的位置有什么特点 它们的两边所在的位置有什么特点
高效课堂
∠2和∠3,∠3和∠4,∠4和∠1.
图中还有邻补角吗
高效课堂
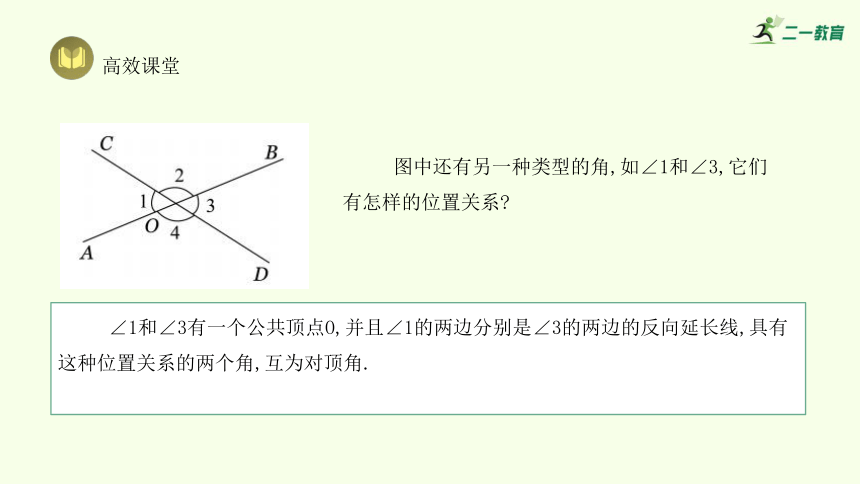
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有另一种类型的角,如∠1和∠3,它们有怎样的位置关系
高效课堂
∠2和∠4.
图中还有对顶角吗
高效课堂
练习
都不是.
两个角除了有一条公共边之外,它们的另一边互为反向延长线.
高效课堂
只有图3是.
对顶角形成的前提条件是两条直线相交.
高效课堂
∠BOF
∠EOC,∠DOF
一个角的对顶角最多只能有一个.
而一个角的邻补角最多可以有两个.
高效课堂
活动二:性质探究
数量关系和位置关系是我们研究几何图形时常见的两个研究方向,前面我们研究了邻补角和对顶角这两类具有特殊位置关系的角.
在前面分类时,已经有同学关注到它们的数量关系,接下来研究这两类角具有怎样的数量关系,以及为什么有着这样的数量关系.
高效课堂
说一说,∠1和∠2为什么互补呢
因为∠1和∠2有一条公共边OC,它们的另一边互为反向延长线,所以平角∠AOB 就是∠1和∠2的和,即∠1+∠2=180°,因此∠1和∠2互补.
高效课堂
说一说,∠1和∠3这对对顶角有怎样的数量关系 你是怎么得到的
∠1=∠3.通过观察、测量等活动得到的.
高效课堂
你能用说理的方法推出∠1=∠3吗
因为∠1与∠2互补,∠3与∠2互补,
所以∠1=∠3(同角的补角相等).
同理,∠2=∠4.
对顶角的性质:对顶角相等.
高效课堂
活动三:知识迁移与应用
(1)因为∠1=∠3(对顶角相等),且∠1+∠3=80°,
高效课堂
活动三:知识迁移与应用
变式: 在上图中,
高效课堂
高效课堂
活动三:知识迁移与应用
高效课堂
活动三:知识迁移与应用
活动三:知识迁移与应用
课堂评价
B
活动三:知识迁移与应用
课堂评价
40°
130°
课堂总结
1.对比邻补角和对顶角,它们有什么异同
2.今天主要学习邻补角和对顶角的知识,我们是从哪几个方面研究的
作业设计
基础性作业:教材练习第1~3题.
提高性作业:教材习题7.1第5,9题.
作业设计
拓展性作业:将一根玻璃棒放入盛有水的烧杯中,一头露出水面,一头浸入水中,我们可以发现浸入水中的部分“变弯了”,它真的变弯了吗 其实没有,这只是光的折射现象,即光从空气射入水中,光线的传播方向发生了改变.如图,一束光AO 射入水中,在水中的传播路径为OB,∠1与∠2是对顶角吗 如果不是对顶角,你能比较它们的大小吗
https://www.21cnjy.com/recruitment/home/fine

展开更多......

收起↑