 资源简介
资源简介
(共28张PPT)
23.3.4 相似三角形的应用
学习目标
1. 掌握相似三角形的应用(难点)
2.能正确分析实际问题中的数量关系进行计算或证明(重点)
3.能运用相似三角形的性质和判定解决实际生活中的高度和宽度等类问题(重点)
新课导入
人们从很早开始,就懂得利用相似三角形的有关性质来计算那些不能直接测量的物体高度和两地距离.
如图所示,利用所学的知识,如何测量旗杆的高度和河流的宽度?
新课学习
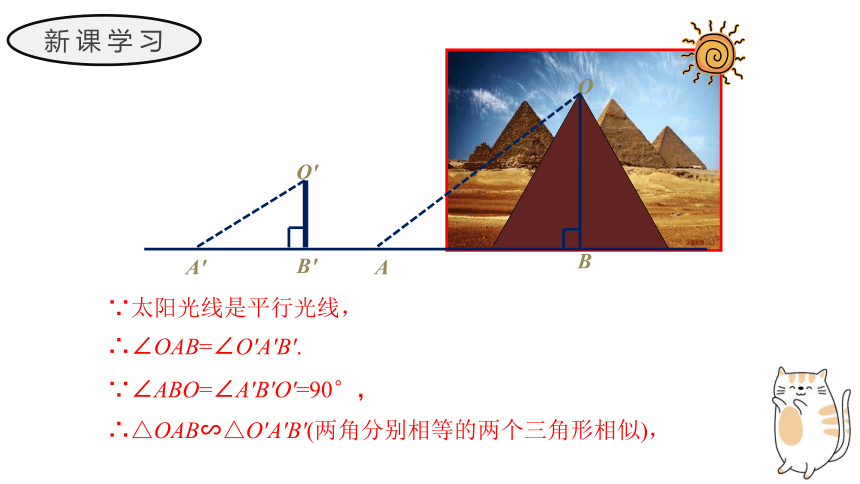
例1:古代一位数学家想出了一种测量金字塔高度的方法:如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O'B',比较木棒的影长A'B'与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O'B'=1 米,A'B'=2米,AB=274 米,求金字塔的高度OB.
新课学习
O
B
A
O′
B′
A′
∵太阳光线是平行光线,
∴∠OAB=∠O′A′B′.
∵∠ABO=∠A′B′O′=90°,
∴△OAB∽△O′A′B′(两角分别相等的两个三角形相似),
新课学习
∴
∴
答:金字塔的高度OB为137米.
金字塔的影长AB为露在外面的影长AC与金字塔底边的一半CB的长度的和.
新课学习
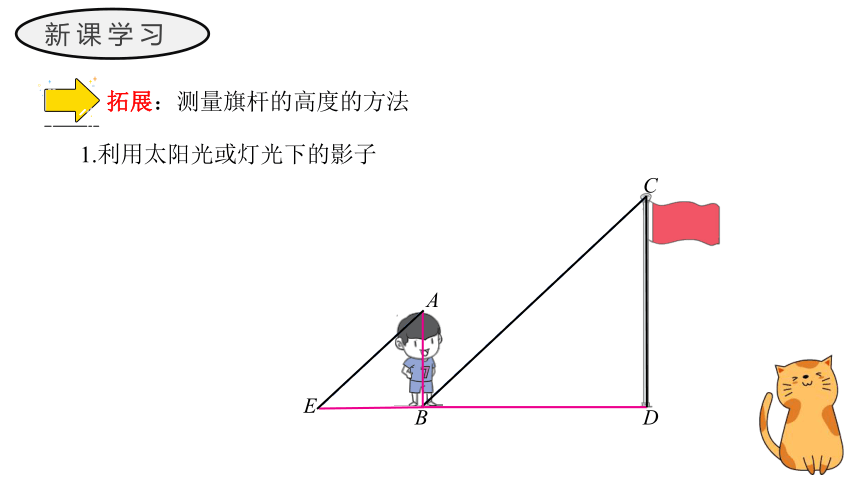
拓展:测量旗杆的高度的过程
(1) 依据:同一时刻,物体的高度与它们的影长成比例.
(2) 测量.让一名身高为h的同学恰好站在旗杆的影子的顶端,然后测量该同学的影长l1,同时测量旗杆 的影长l2.
(3) 计算.
新课学习
拓展:测量旗杆的高度的方法
1.利用太阳光或灯光下的影子
A
B
C
D
E
新课学习
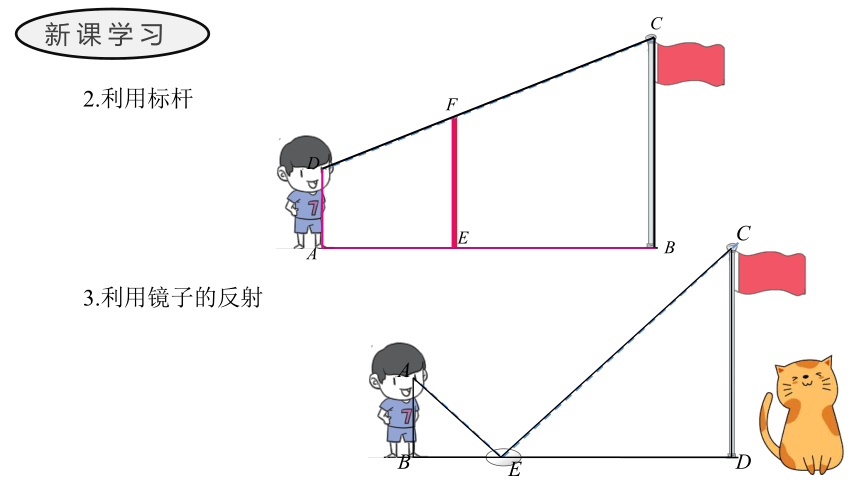
2.利用标杆
C
D
E
F
B
A
A
B
C
D
E
3.利用镜子的反射
新课学习
例2:如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选定点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=118米,DC =61米,EC =50米,求河的宽度AB.(精确到0.1米)
新课学习
∵∠ADB=∠EDC,∠ABD=∠ECD=90°,
∴△ABD∽△ECD(两角分别相等的两个三角形相似),
∴
解得
答:河的宽度AB约为为96.7米.
新课学习
例3:如图,已知D、E分别是△ABC的边AB、AC上的点,且∠ADE=∠C.求证:AD·AB=AE·AC.
∵∠ADE=∠C,∠A=∠A,
∴△ADE∽△ACB(两角分别相等的两个三角形相似),
∴
∴AD·AB=AE·AC.
利用相似三角形可以证明几条线段之间的乘积关系
新课学习
拓展:利用相似三角形证明等积式的步骤
1.将等积式转化为比例式
2.观察比例式中的线段是否在两个形状相同的三角形中(三点定形法)
(1)如果在两个形状相同的三角形中,则证明这两个三角形相似
(2)如果不在两个形状相同的三角形中,则利用如下方法转化:①等线段转化;②中间比转化;③添加辅助线构造相似三角形转化
3.根据相似三角形或转化得到比例式,再化为等积式
新课学习
拓展:相似三角形的应用主要有两个方面
1.测高(不能直接使用皮尺或刻度尺测量):测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
2.测距(不能直接测量的两点间的距离): 测量不能到达两点间的距离,常构造相似三角形求解.
新课学习
拓展:解相似三角形实际问题的一般步骤
1.审题;
2.构建图形;
3.利用相似解决问题.
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
2米
课堂总结
1.测量旗杆的高度的过程
2.测量旗杆的高度的方法
3.利用相似三角形证明等积式的步骤
4.解相似三角形实际问题的一般步骤
THANK YOU
展开更多......
收起↑
 资源预览
资源预览






 资源预览
资源预览








