资源简介

(共34张PPT)
第11课时　平面直角坐标系与函数的概念
第三章 函数
1.了解坐标平面内的点与有序实数对的一一对应关系，理解平
面直角坐标系的有关概念，能画出平面直角坐标系；在给定的平
面直角坐标系中，能根据坐标描出点的位置，由点的位置写出它
的坐标.
2.会运用对称点的坐标之间的关系解答问题.
3.了解函数的意义和函数的三种表示方法，能结合图象对简单
实际问题中的函数关系进行分析.
4.会确定函数解析式中自变量的取值范围，并会求出函数值.
5.能用适当的函数表示法描述简单实际问题中变量之间的关
系.
1.各象限内点的坐标的符号特征：
点 P(a，b)在_________ a>0，b>0；点P在__________ a<0，
b>0；点 P 在__________ a<0，b<0；点 P 在__________ a>0，
b<0; 点 P 在 x 轴上 a 为任意实数，b＝0；点 P 在 y 轴上 a＝0，
b 为任意实数；点 P 在第一、第三象限坐标轴夹角平分线上 a＝
b；点 P 在第二、第四象限坐标轴夹角平分线上 a＝－b.
第一象限
第二象限
第三象限
第四象限
2.已知点 A 的坐标为(x，y).若点 A，B 关于 x 轴对称，则点 B
的坐标为______________；若点 A，B 关于 y 轴对称，则点 B 的坐
标为______________； 若点 A，B 关于原点对称，则点 B 的坐标
为____________.
(x，－y)
(－x，y)
(－x，－y)
3.函数的三种表示法：解析法、列表法和__________.画函数
图象的一般步骤：列表、描点和________.
图象法
连线
4.自变量的取值必须使含自变量的代数式有意义.
坐标的符号特征
1.(2023·丽水)在平面直角坐标系中，点 P(－1，m2 ＋1)位于
(
)
B.第二象限
D.第四象限
A.第一象限
C.第三象限
答案：B
函数自变量的取值范围
答案：D
函数的图象
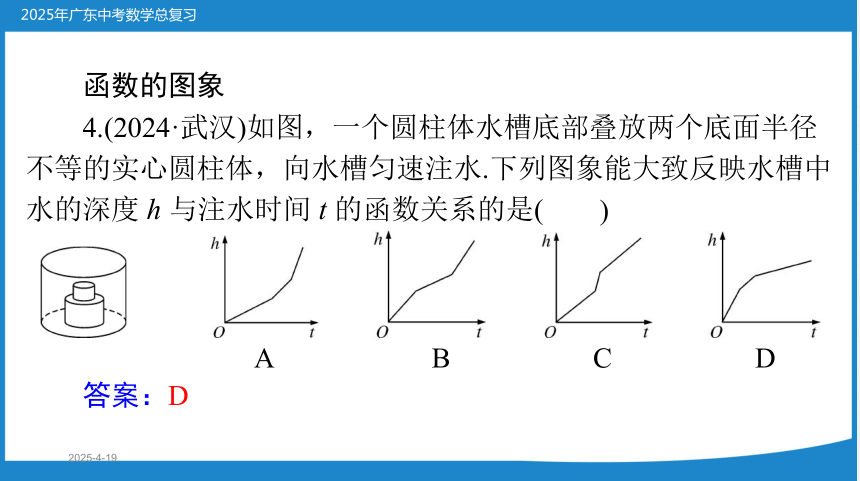
4.(2024·武汉)如图，一个圆柱体水槽底部叠放两个底面半径
不等的实心圆柱体，向水槽匀速注水.下列图象能大致反映水槽中
水的深度 h 与注水时间 t 的函数关系的是(
)
A
B
C
D
答案：D
1.对称点的坐标之间的符号关系.
2.函数自变量的取值范围考虑要周全.表示实际问题时，自变
量的取值必须使实际问题有意义.
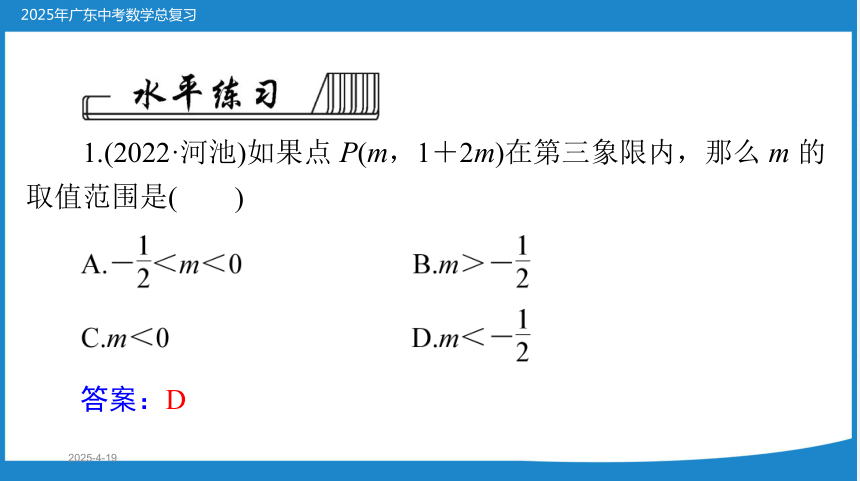
1.(2022·河池)如果点 P(m，1＋2m)在第三象限内，那么 m 的
取值范围是(
)
答案：D
2.下列函数中，自变量 x 的取值范围是 x＞3 的是(
)
答案：B
3.(2022·广东)在平面直角坐标系中，将点(1，1)向右平移 2 个
单位长度后，得到的点的坐标是(
)
B.(－1，1)
D.(1，－1)
A.(3，1)
C.(1，3)
答案：A
4.(2024·贵州)为培养青少年的科学态度和科学思维，某校创
建了“科技创新”社团.小红将“科”“技”“创”“新”写在如
图所示的方格纸中，若建立平面直角坐标系，使“创”“新”的
坐标分别为(－2，0)，(0，0)，则“技”所在的象限为(　　)
A.第一象限　　B.第二象限　　C.第三象限　　D.第四象限
答案：A
5.(2024·广西)如图，在平面直角坐标系中，点 O 为坐标原点，
点 P 的坐标为(2，1)，则点 Q 的坐标为(
)
A.(3，0)
B.(0，2)
C.(3，2)
D.(1，2)
答案：C
6.(2023·广安)如图所示，用弹簧测力计将一铁块悬于盛有水
的水槽中，然后匀速向上提起，使铁块完全露出水面，并上升一
定高度.下列能反映弹簧测力计的读数 y(单位：N)与铁块被提起的
时间 x(单位：s)之间的函数关系的大致图象是(
)
A
B
C
D
答案：A
7.(2022·潍坊)地球周围的大气层阻挡了紫外线和宇宙射线对
地球生命的伤害，同时产生一定的大气压，海拔不同，大气压不
同.观察图中数据，你发现(
)
A.海拔越高，大气压越大
B.图中曲线是反比例函数的图象
C.海拔为 4 千米时，大气压约为
70 千帕
D.图中曲线表达了大气压和海拔两个量之间的变化关系
答案：D
8.2025 年第九届亚洲冬季运动会将在哈尔滨举行.如图是本届
亚洲冬季运动会的会徽“超越”，将其放在平面直角坐标系中，若
A，C 两点的坐标分别为(2，1)，(0，2)，则点 B 的坐标为______.
答案：(－1，－2)
10.在平面直角坐标系中，若点 M(1，3)与点 N(x，3)之间的距
离是 5，则 x 的值是__________.
答案：－4 或 6
11.某自行车存车处某日的存车量为 4 000 辆次，其中变速车
存车费是每辆一次 0.30 元，普通车存车费是每辆一次 0.20 元.若该
日普通车存车量为 x 辆次，则该日存车费总收入 y(元)与 x(辆次)
的函数关系式是____________________.
答案：y＝－0.1x＋1 200(0≤x≤4 000)
12.(2023·滨州)如图，在平面直角坐标系中，△ABO 的三个顶
点的坐标分别为 A(6，3)，B(6，0)，O(0，0).若将△ABO 向左平移
3 个单位长度后得到△CDE，则点 A 的对应点 C 的坐标是______.
答案：(3，3)
13.已知：点 P(2m＋4，m－1).试分别根据下列条件，求出点 P
的坐标.
(1)点 P 在过点 A(－2，－3)且与 y 轴平行的直线上.
(2)点 P 在第四象限内，且到 x 轴的距离是它到 y 轴距离的一
半.
解：(1)2m＋4＝－2，解得 m＝－3.
∴m－1＝－4.∴P(－2，－4).
14.小明某天上午 9 时骑自行车离开家，15 时回到家，他描绘
了离家的距离随时间的变化情况(如图).
(1)图象表示了哪两个变量间的关系？
(2)10 时和 13 时，他分别离家多远？
(3)他到达离家最远的地方是什么时间？离家多远？
(4)11 时到 12 时他骑行了多少千米？
(5)他可能在哪段时间内休息，并吃午餐？
(6)他由离家最远的地方返回家的平均速度是多少？
解：(1)时间与距离.
(2)10 时和 13 时，分别离家 10 千米和 30 千米.
(3)12 时到达离家最远的地方，离家 30 千米.
(4)11 时到 12 时，他骑行了 12 千米.
(5)他可能在 12 时到 13 时休息，并吃午餐.
(6)平均速度为 15 千米/时.
销售量 n/件 n＝50－x
销售单价 m/元
15.某网店尝试用单价随天数而变化的销售模式销售一种商
品，利用 30 天的时间销售一种成本为 10 元/件的商品，经过统计
得到销售该商品第 x 天(x 为正整数)的相关信息，如表所示：
(1)请计算销售第几天该商品单价为 25 元.
(2)求网店销售该商品 30 天中单日所获利润 y(元)关于 x(天)的
函数解析式.
(3)这 30 天中第几天获得的利润最大？最大利润是多少？
解：(1)第 10 天或第 28 天.
(3)第 15 天获得的利润最大，最大利润为 612.5 元.
x/h … 11 12 13 14 15 16 17 18 …
y/cm … 189 137 103 80 101 133 202 260 …
16.(2022·舟山)某日，一港口的潮水高度 y(cm)和时间 x(h)的部
分数据及函数图象如下：
(1)数学活动：
①根据表中数据，通过描点、连线(光滑曲线)的方式补全该函
数的图象.
②观察函数图象，当 x＝4 时，y 的值为多少？当 y 的值最大
时，x 的值为多少？
(2)数学思考：
请结合函数图象，写出该函数的两条性质或结论.
(3)数学应用：
根据研究，当潮水高度超过 260 cm 时，货轮能够安全进出该
港口.当天什么时间段适合货轮进出此港口？
解：(1)①描点、连线补全该函数图象如图所示：
②通过观察函数图象，当 x＝4 时，y＝200，当 y 的值最大时，
x＝21.
(2)该函数的两条性质如下(答案不唯一)：
①当 2≤x≤7 时，y 随 x 的增大而增大；
②当 x＝14 时，y 的值最小.
(3)由图象可知，当 y＝260 时，x＝5 或 x＝10 或 x＝18 或 x＝
23，
∴当 5＜x＜10 或 18＜x＜23 时，y＞260.
即当天 5 时至 10 时，18 时至 23 时，适合货轮进出此港口.

展开更多......

收起↑