资源简介

中小学教育资源及组卷应用平台
小升初必考专题10：比和比例-2025年六年级下册通用版
一、选择题
1．比例尺是1∶5000000表示地图上1cm距离相当于实际距离（ ）。
A．50m B．50km C．5km D．500km
2．一辆自行车，前齿轮齿数为32，后齿轮齿数为12。当前齿轮转数是3转时，后齿轮转数是（ ）转。
A．8 B．9 C．10 D．12
3．如果＝（A、B均不为0），那么A∶B＝（ ）。
A．2024∶2025 B．2023∶2022 C．2023∶1011 D．1011∶2023
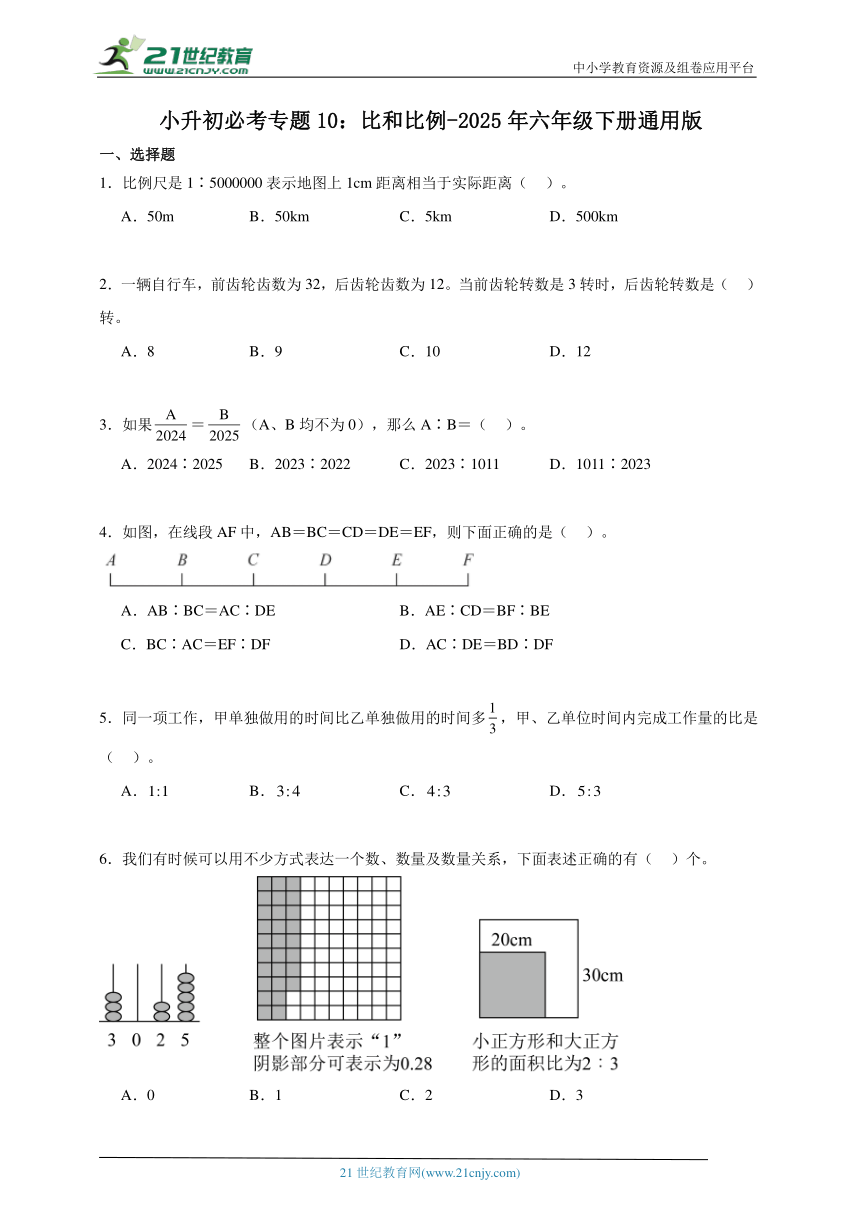
4．如图，在线段AF中，AB＝BC＝CD＝DE＝EF，则下面正确的是（ ）。
A．AB∶BC＝AC∶DE B．AE∶CD＝BF∶BE
C．BC∶AC＝EF∶DF D．AC∶DE＝BD∶DF
5．同一项工作，甲单独做用的时间比乙单独做用的时间多，甲、乙单位时间内完成工作量的比是（ ）。
A． B． C． D．
6．我们有时候可以用不少方式表达一个数、数量及数量关系，下面表述正确的有（ ）个。
A．0 B．1 C．2 D．3
7．羽毛球兴趣小组中男生人数与女生人数的比是3∶2，男生人数占总人数的（ ）%。
A．20 B．30 C．60 D．150
8．小黑兔的只数是40的，小白兔只数的是40，小黑兔的只数与小白兔的只数的比是（ ）。
A．1∶1 B．16∶25 C．25∶16 D．4∶5
二、填空题
9．如果（、均不为0），那( )∶( )。
10．
一条路，已修，还剩，已修的和还剩的比是（ ）∶（ ）。
11．有杂志和故事书各150本，再添置( )本杂志，才能使杂志和故事书的比是3∶2。
12．某小区1号楼的实际高度为35m，与模型高度的比是50∶1，模型的高度是( )cm。
13．在比例尺是的地图上，实际距离360千米在图上应画( )厘米，图上距离4.5厘米表示实际距离( )千米。
14．将一个长8厘米、宽6厘米的长方形按1∶2的比缩小后，长是( )厘米，宽是( )厘米；如果将它按2∶1的比放大，长是( )厘米，宽是( )厘米。
15．张师傅加工零件情况如下表。
加工时间/时 1 2 3 4 5 6
加工总数/个 20 40 60 80 100 120
上表中( )和( )是两种相关联的量，( )随着( )的变化而变化。因为( )是一定的，所以加工总数和加工时间成( )比例。
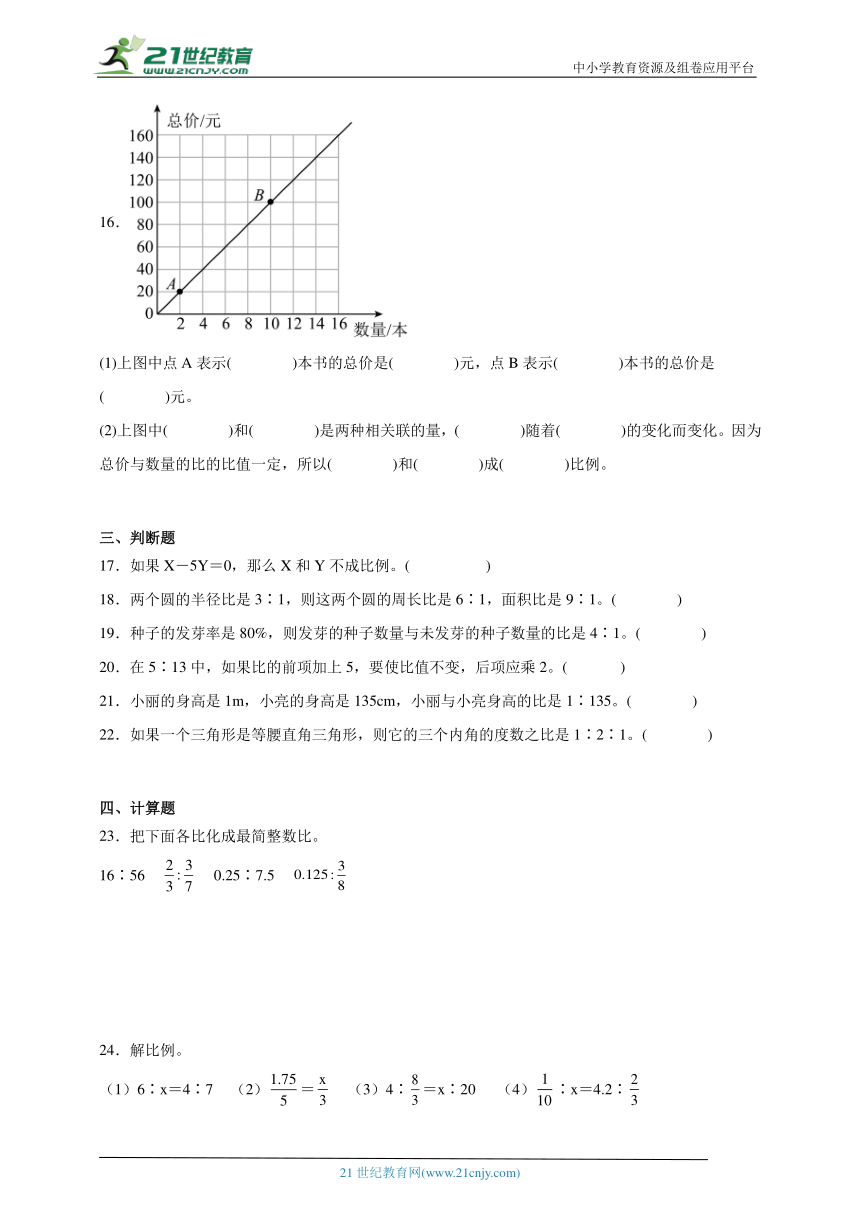
16．
(1)上图中点A表示( )本书的总价是( )元，点B表示( )本书的总价是( )元。
(2)上图中( )和( )是两种相关联的量，( )随着( )的变化而变化。因为总价与数量的比的比值一定，所以( )和( )成( )比例。
三、判断题
17．如果X－5Y＝0，那么X和Y不成比例。( )
18．两个圆的半径比是3∶1，则这两个圆的周长比是6∶1，面积比是9∶1。( )
19．种子的发芽率是80%，则发芽的种子数量与未发芽的种子数量的比是4∶1。( )
20．在5∶13中，如果比的前项加上5，要使比值不变，后项应乘2。( )
21．小丽的身高是1m，小亮的身高是135cm，小丽与小亮身高的比是1∶135。( )
22．如果一个三角形是等腰直角三角形，则它的三个内角的度数之比是1∶2∶1。( )
四、计算题
23．把下面各比化成最简整数比。
16∶56 0.25∶7.5
24．解比例。
（1）6∶x＝4∶7 （2）＝ （3）4∶＝x∶20 （4）∶x＝4.2∶
五、解答题
25．小明从一幅比例尺是1∶12000000的地图上量得他家到北京的距离是4厘米，他家到北京的实际距离是多少千米？
26．在一幅比例尺为1∶5000000的地图上，量得A、B两地的距离是12厘米。甲、乙两车分别从A、B两地同时出发，相向而行，经过4小时相遇。已知甲车的速度是每小时70千米，求乙车的速度。
27．用一根长48分米的铁丝做一个长方体的框架，使它的高为8分米，长、宽的比是1∶1。再把它的侧面和底面糊上纸，做成一个长方体的灯笼，至少需要多少平方分米的纸？
28．一辆货车从甲地开往乙地，第一天行了全程的20%，第二天行了360千米，这时已行路程和剩下路程的比是3∶2，甲、乙两地相距多少千米？
29．水果店运来苹果、梨和香蕉一共450千克，其中运来的梨的质量占三种水果的，运来苹果的质量和香蕉的质量比是2∶1，运来苹果、梨、香蕉各多少千克？
30．运输队向灾区运送120吨救灾物资。
（1）如果要一次把救灾物资全部运出，卡车的载质量与所需卡车的数量如下表，把表格填写完整。
载质量/吨 2.5 4 5 10 …
数量/辆 48 30 …
①卡车的载质量和所需卡车的数量成什么比例？为什么？
②如果用载质量是6吨的卡车来运，一共需要多少辆？
（2）如果用8辆载质量是2.5吨的卡车来运，运输的次数和所运救灾物资的质量如下表，把表格填写完整。
次数 1 2 3 4 5 6 …
质量/吨 …
运输的次数和所运物资的质量成什么比例？为什么？
（3）如果用6辆载质量是4吨的卡车来运，多少次能把这批救灾物资运完？
《小升初必考专题10：比和比例-2025年六年级下册通用版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A A C B C C B
1．B
【分析】图上距离与实际距离的比叫做比例尺。据此可知：比例尺是1∶5000000表示实际距离是图上距离的5000000倍。用图上距离×5000000即可得实际距离。再根据1km＝100000cm，将结果换算成以km为单位即可。
【详解】1×5000000＝5000000（cm）
5000000cm＝50km
比例尺是1∶5000000表示地图上1cm距离相当于实际距离50km。
故答案为：B
2．A
【分析】在同一时间内，自行车的两个齿轮转动的总齿数是相同的，即每个齿轮的齿数×转数＝转过的总齿数（一定），乘积一定，则每个齿轮的齿数与转数成反比例关系，据此列出反比例方程，并求解。
【详解】解：设当前齿轮转数是3转时，后齿轮转数是转。
12＝32×3
12＝96
12÷12＝96÷12
＝8
当前齿轮转数是3转时，后齿轮转数是8转。
故答案为：A
3．A
【分析】根据比例的基本性质“两个外项的积等于两个内项的积”，先将比例式改写成乘法的形式，再将其改写成A∶B的比例式即可。
【详解】由＝可得：2025A＝2024B，那么A∶B＝2024∶2025。
故答案为：A
4．C
【分析】根据题意设AB＝BC＝CD＝DE＝EF＝1，分别求出各选项等号两边的比的比值，再判断是否相等即可解答。
【详解】A．AB∶BC＝1∶1＝1，AC∶DE＝2∶1＝2，AB∶BC≠AC∶DE。该选项错误。
B．AE∶CD＝4∶1＝4，BF∶BE＝4∶3＝，AE∶CD≠BF∶BE。该选项错误。
C．BC∶AC＝1∶2＝0.5，EF∶DF＝1∶2＝0.5，BC∶AC＝EF∶DF。该选项正确。
D．AC∶DE＝2∶1＝2，BD∶DF＝2∶2＝1，AC∶DE≠BD∶DF。该选项错误。
故答案为：C
5．B
【分析】单位时间内完成工作量即工作效率。将乙的工作时间看作单位“1”，甲的工作时间是1＋＝，根据工作总量÷工作时间＝工作效率，分别代入数据，求出他们的工作效率。再根据比的意义，求出效率比即可。
【详解】甲：1÷（1＋）
＝1÷
＝1×
＝
乙：1÷1＝1
∶1
＝（×4）∶（1×4）
＝3∶4
甲、乙单位时间内完成工作量的比是3∶4。
故答案为：B
6．C
【分析】（1）每个小算珠表示1，千位上有3个表示3个千，十位上有2个表示2个十，个位上有5个表示5个一。据此判断。
（2）正方形被平均分成了100个小格，其中一个小格为这个正方形的，用小数表示为0.01。数出阴影部分占的小格子数，即可判断。
（3）正方形的面积＝边长×边长，据此计算出两个正方形的面积，再根据比的意义，写出比即可判断。
【详解】根据分析可得：
A．表示的3025，原表述是正确的；
B．整个图片表示“1”，阴影部分有28个小格，可表示为0.28，原表述是正确的；
C．小正方形的面积：20×20＝400（cm2）
大正方形的面积：30×30＝900（cm2）
小正方形和大正方形的面积比是400∶900＝4∶9，原表述不正确。
即正确的表述有2个。
故答案为：C
7．C
【分析】根据比的意义，把男生人数看作3份，女生人数看作2份，则总人数有份，根据求一个数占另一个数的百分之几，用一个数除以另一个数。据此解答。
【详解】
男生人数占总人数的60%。
故答案为：C
8．B
【分析】已知小黑兔的只数是40的，根据求一个数的几分之几是多少，根据分数乘法的意义求出小黑兔的只数；
已知小白兔只数的是40，根据已知一个数的几分之几是多少，求这个数，根据分数除法的意义求出小白兔的只数；
根据比的意义写出小黑兔的只数与小白兔的只数的比，再化简比。
【详解】小黑兔：40×＝32（只）
小白兔：40÷＝40×＝50（只）
32∶50＝（32÷2）∶（50÷2）＝16∶25
小黑兔的只数与小白兔的只数的比是16∶25。
故答案为：B
9． 6 5
【分析】在比例中，两个外项的积等于两个内项的积，这叫做比例的基本性质。从题意可知：可以看作两个外项相乘， 可以看作两个内项相乘，据此列出比例即可。
【详解】如果（、均不为0），那∶＝6∶5。
10．；；5；2
【分析】把全长看作单位“1”，平均分成7份，已修的长度占5份，用分数表示为；还剩的长度占2份，用分数表示为；再根据比的意义写出已修的和还剩的比，并化简比。
【详解】∶
＝（×7）∶（×7）
＝5∶2
一条路，已修（），还剩（），已修的和还剩的比是（5）∶（2）。
11．75
【分析】分析题目，根据比的意义用故事书的本数150除以对应的份数2即可求出一份是多少本，再乘杂志的份数3即可得到添置后杂志的本数，最后用添置后杂志的本数减去原来的杂志本数150即可解答。
【详解】150÷2×3－150
＝75×3－150
＝225－150
＝75（本）
有杂志和故事书各150本，再添置75本杂志，才能使杂志和故事书的比是3∶2。
12．70
【分析】根据实际高度与模型高度的比，可知实际高度是模型高度的50倍，我们可以用实际高度除以50得到模型高度，最后注意单位换算。
【详解】35÷50＝0.7（m）
0.7×100＝70（cm）
所以模型的高度是70cm。
13． 12 135
【分析】由线段比例尺可知，图上1厘米代表实际距离30千米，先把线段比例尺转化为数值比例尺，再根据“图上距离＝实际距离×比例尺”求出图上距离，然后根据“实际距离＝图上距离÷比例尺”求出实际距离，据此解答。
【详解】图上距离∶实际距离
＝1厘米∶30千米
＝1厘米∶3000000厘米
＝1∶3000000
360千米＝36000000厘米
36000000×＝12（厘米）
4.5÷
＝4.5×3000000
＝13500000（厘米）
13500000厘米＝135千米
所以，实际距离360千米在图上应画12厘米，图上距离4.5厘米表示实际距离135千米。
14． 4 3 16 12
【分析】把图形按照n∶1放大，就是将图形的每一条边放大到原来的n倍，放大后图形与原图形对应边长的比是n∶1；把图形按照1∶n缩小，就是将图形的每一条边缩小到原来的，缩小后图形与原图形对应边长的比是1∶n，据此解答。
【详解】①按1∶2的比缩小
长：8÷2＝4（厘米）
宽：6÷2＝3（厘米）
②按2∶1的比放大
长：8×2＝16（厘米）
宽：6×2＝12（厘米）
因此将一个长8厘米、宽6厘米的长方形按1∶2的比缩小后，长是4厘米，宽是3厘米；如果将它按2∶1的比放大，长是16厘米，宽是12厘米。
15． 加工时间 加工总数 加工总数 加工时间 加工总数与加工时间的比值 正
【分析】两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定（也就是商一定），这两种量成正比例关系。
【详解】20∶1＝40∶2＝60∶3＝80∶4＝100∶5＝120∶6＝20（一定）
上表中（加工时间）和（加工总数）是两种相关联的量，（加工总数）随着（加工时间）的变化而变化。因为（加工总数与加工时间的比值）是一定的，所以加工总数和加工时间成（正）比例。
16．(1) 2 20 10 100
(2) 数量 总价 总价 数量 总价 数量 正
【分析】（1）根据图示，分别根据A点和B点所在的列和行表示的数填空即可；
（2）两种相关联的量，一种量变化，另一种量也随着变化，如果这两个量中相对应的两个数的比值一定，这两种量叫作成正比例的量，它们的关系叫作正比例关系，用式子表示为：＝k；据此结合表格中给出的数据解答即可。
【详解】（1）上图中点A表示2本书的总价是20元，点B表示10本书的总价是100元。
（2）上图中数量和总价是两种相关联的量，总价随着数量的变化而变化。因为总价与数量的比的比值一定，所以总价和数量成正比例。
17．×
【分析】把X－5Y＝0转化为的形式，两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫作成正比例的量，它们的关系叫作正比例关系。如果用字母和表示两种相关联的量，用表示它们的比值（一定），正比例关系可以用表示，据此解答。
【详解】因为X－5Y＝0，所以X＝5Y，即（一定），那么X和Y成正比例。
故答案为：×
18．×
【分析】设小圆的半径为r，则大圆的半径为3r，分别代入圆的周长＝2πr和圆的面积＝πr2，表示出各自的周长和面积，即可求解。
【详解】假设小圆的半径为r，则大圆的半径为3r，
大圆的周长：2π×3r＝6πr
小圆的周长：2πr
6πr∶2πr＝3∶1
大圆的面积：π（3r）2＝9πr2
小圆的面积：πr2
9πr2∶πr2＝9∶1
那么这两个圆的周长比是3∶1，这两个圆的面积的比是9∶1，原题说法错误。
故答案为：×
19．√
【分析】把种子的总数量看作单位“1”，发芽率表示发芽种子的数量占种子总数量的百分率，种子的发芽率是80%，则未发芽的种子数量占种子总数量的（1－80%），再根据比的意义求出发芽的种子数量与未发芽的种子数量的最简整数比，据此解答。
【详解】80%∶（1－80%）
＝80%∶20%
＝0.8∶0.2
＝（0.8÷0.2）∶（0.2÷0.2）
＝4∶1
所以，发芽的种子数量与未发芽的种子数量的比是4∶1。
故答案为：√
20．√
【分析】根据比的基本性质：比的前项和后项同时乘或除以一个不为0的数，比值不变；用比的前项＋5，再除以比的前项，求出比的前项扩大到原来的几倍，则比的后项也扩大到原来的几倍，据此解答。
【详解】（5＋5）÷5
＝10÷5
＝2
在5∶13中，如果比的前项加上5，要使比值不变，后项应乘2。
原题干说法正确。
故答案为：√
21．×
【分析】已知小丽的身高是1m，小亮的身高是135cm，先根据进率“1m＝100cm”把小丽的身高换算成以“cm”作单位的数；再根据比的意义写出小丽与小亮身高的比，并化简比，化简整数比的方法：根据比的基本性质，把比的前项、后项同时除以它们的最大公因数，使比化简；据此解答。
【详解】1m∶135cm
＝（1×100）cm∶135cm
＝100∶135
＝（100÷5）∶（135÷5）
＝20∶27
小丽与小亮身高的比是20∶27。
原题说法错误。
故答案为：×
22．√
【分析】已知三角形的内角和是180°，等腰直角三角形两个锐角相等，且两个锐角的度数和是90°，所以等腰直角三角形的三个内角分别是45°、90°、45°，根据比的意义写出三个内角的度数之比，并化简比，据此判断。
【详解】等腰直角三角形的三个内角分别是45°、90°、45°。
45°∶90°∶45°
＝（45°÷45°）∶（90°÷45°）∶（45°÷45°）
＝1∶2∶1
如果一个三角形是等腰直角三角形，则它的三个内角的度数之比是1∶2∶1。
原题说法正确。
故答案为：√
23．2∶7；14∶9；1∶30；1∶3
【分析】化简比的方法：根据比的基本性质，比的前项和后项同时乘一个数或除以一个数（0除外）比值不变。据此解答。
【详解】
＝
＝14∶9
＝1∶3
24．（1）x＝10.5；（2）x＝1.05；（3）x＝30；（4）x＝
【分析】（1）6∶x＝4∶7，解比例，原式化为：4x＝6×7，再根据等式的基本性质2，方程两边同时除以4即可。
（2）＝，解比例，原式化为：5x＝1.75×3，再根据等式的性质2，方程两边同时除以5即可。
（3）4∶＝x∶20，解比例，原式化为：x＝4×20，再根据等式的性质2，方程两边同时除以即可。
（4）∶x＝4.2∶，解比例，原式化为：4.2x＝×，再根据等式的性质2，方程两边同时除以4.2即可。
【详解】（1）6∶x＝4∶7
解：4x＝6×7
4x＝42
4x÷4＝42÷4
x＝10.5
（2）＝
解：5x＝1.75×3
5x＝5.25
5x÷5＝5.25÷5
x＝1.05
（3）4∶＝x∶20
解：x＝4×20
x＝80
x÷＝80÷
x＝80×
x＝30
（4）∶x＝4.2∶
解：4.2x＝×
4.2x＝
4.2x÷4.2＝÷4.2
x＝÷
x＝×
x＝
25．480千米
【分析】分析题目，先根据实际距离＝图上距离÷比例尺求出小明家到北京的实际距离，再根据1千米＝100000厘米把实际距离换算成以千米为单位即可。
【详解】4÷
＝4×12000000
＝48000000（厘米）
48000000厘米＝480千米
答：他家到北京的实际距离是480千米。
26．80千米
【分析】已知图上距离÷比例尺＝实际距离，求出实际距离，再根据“路程÷相遇时间＝速度和”，再用速度和减去甲车的速度即可求出乙车的速度。
【详解】12÷
＝12×5000000
＝60000000（厘米）
60000000厘米＝600千米
600÷4－70
＝150÷70
＝80（千米）
答：乙车的速度是每小时80千米。
27．68平方分米
【分析】根据长方体的棱长总和＝（长＋宽＋高）×4，用棱长总和除以4求出长、宽、高的和，高已知，用长、宽、高的和减去高，求出长与宽的和，然后利用按比例分配的方法，把长看作1份、宽看作1份，用长与宽的和除以长、宽的份数和，再分别乘它们的份数，即可求出长与宽；把它的侧面和底面糊上纸，做成一个长方体的灯笼，是求剩下5个面的总面积，根据长方体的表面积公式S＝ab＋（ah＋bh）×2求解即可。
【详解】48÷4－8
＝12－8
＝4（分米）
4÷（1＋1）
＝4÷2
＝2（分米）
2×1＝2（分米）
2×1＝2（分米）
2×2＋（2×8＋2×8）×2
＝2×2＋（16＋16）×2
＝2×2＋32×2
＝4＋64
＝68（平方分米）
答：至少需要68平方分米的纸。
28．900千米
【分析】将全程看作单位“1”，根据已行路程和剩下路程的比是3∶2，可以确定两天共行全程的，第二天行了全程的（－20%），第二天行的距离÷对应分率＝全程，据此列式计算。
【详解】360÷（－20%）
＝360÷（－20%）
＝360÷
＝360×
＝900（千米）
答：甲、乙两地相距900千米。
29．苹果240千克；梨90千克；香蕉120千克
【分析】把运来的三种水果的总质量看作单位“1”，根据求一个数的几分之几是多少，用乘法，用450×列式求出运来的梨的质量，再用450减去梨的质量，求出运来的苹果的质量和香蕉的质量和，运来苹果的质量和香蕉的质量比是2∶1，把运来的苹果看作2份，香蕉看作1份，再用运来的苹果的质量和香蕉的质量和除以苹果的质量和香蕉的质量的份数和，求出1份是多少，再分别乘苹果和香蕉的份数即可求出运来苹果、香蕉各多少千克。
【详解】450×＝90（千克）
450－90＝360（千克）
360÷（2＋1）
＝360÷3
＝120（千克）
120×2＝240（千克）
120×1＝120（千克）
＝120（千克）
答：苹果的质量是240千克，梨的质量是90千克，香蕉的质量是120千克。
30．（1）表见详解
①成反比例；原因见详解
②20辆
（2）表见详解；成正比例；原因见详解
（3）5次
【分析】（1）用救灾物质的总质量÷卡车载货物的质量，求出需要卡车的数量，完成表格。
①判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。据此判断。
②根据卡车数量＝货物的总质量÷卡车载货物的质量，用120÷6，即可求出用载质量是6吨的卡车来运，一共需要卡车的数量。
（2）根据货物的总质量＝卡车载货物的质量×运的数量，求出运1辆卡车运货物的质量，2辆卡车运货物的质量，…，求出运6辆卡车运货物的质量，完成表格。
判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。据此判断。
（3）用4×6，求出用6辆卡车一次运货物的质量，再用货物总质量÷6辆卡车一次运货物的质量，即可求出多少次能把这批救灾物资运完。
【详解】（1）120÷5＝24（次）
120÷10＝12（次）
表如下：
载质量/吨 2.5 4 5 10 …
数量/辆 48 30 24 12 …
2.5×48＝4×30＝5×24＝10×12＝120（一定），卡车的载质量和所需卡车的数量成反比例。
答：卡车的载质量和所需卡车的数量成反比例。
②120÷6＝20（辆）
答：一共需要20辆。
（2）2.5×1＝2.5（吨）
2.5×2＝5（吨）
2.5×3＝7.5（吨）
2.5×4＝10（吨）
2.5×5＝12.5（吨）
2.5×6＝15（吨）
表如下：
次数 1 2 3 4 5 6 …
质量/吨 2.5 5 7.5 10 12.5 15 …
2.5∶1＝5∶2＝7.5∶3＝10∶4＝12.5∶5＝15∶6＝2.5（一定），运输的次数和所运物资的质量成正比例。
答：运输的次数和所运物资的质量成正比例。
（3）120÷（4×6）＝120÷24＝5（次）
答：5次能把这批救灾物资运完。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑