资源简介

七年级数学下册新人教版第七章第4节《平移》课时练习
一、单选题
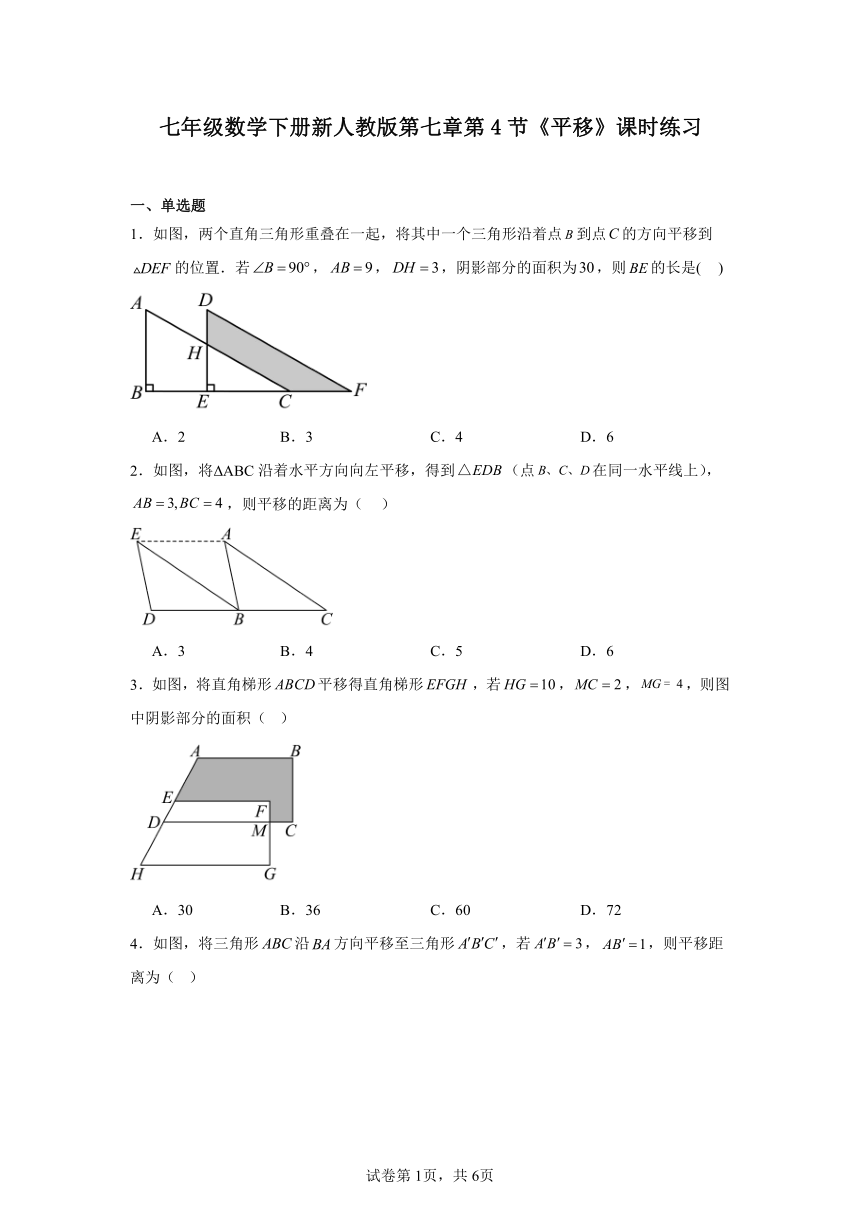
1．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点到点的方向平移到的位置．若，，，阴影部分的面积为，则的长是( )
A．2 B．3 C．4 D．6
2．如图，将ΔABC沿着水平方向向左平移，得到（点在同一水平线上），，则平移的距离为（ ）
A．3 B．4 C．5 D．6
3．如图，将直角梯形平移得直角梯形，若，，，则图中阴影部分的面积（ ）
A．30 B．36 C．60 D．72
4．如图，将三角形沿方向平移至三角形，若，，则平移距离为（ ）
A．2 B．3 C．4 D．5
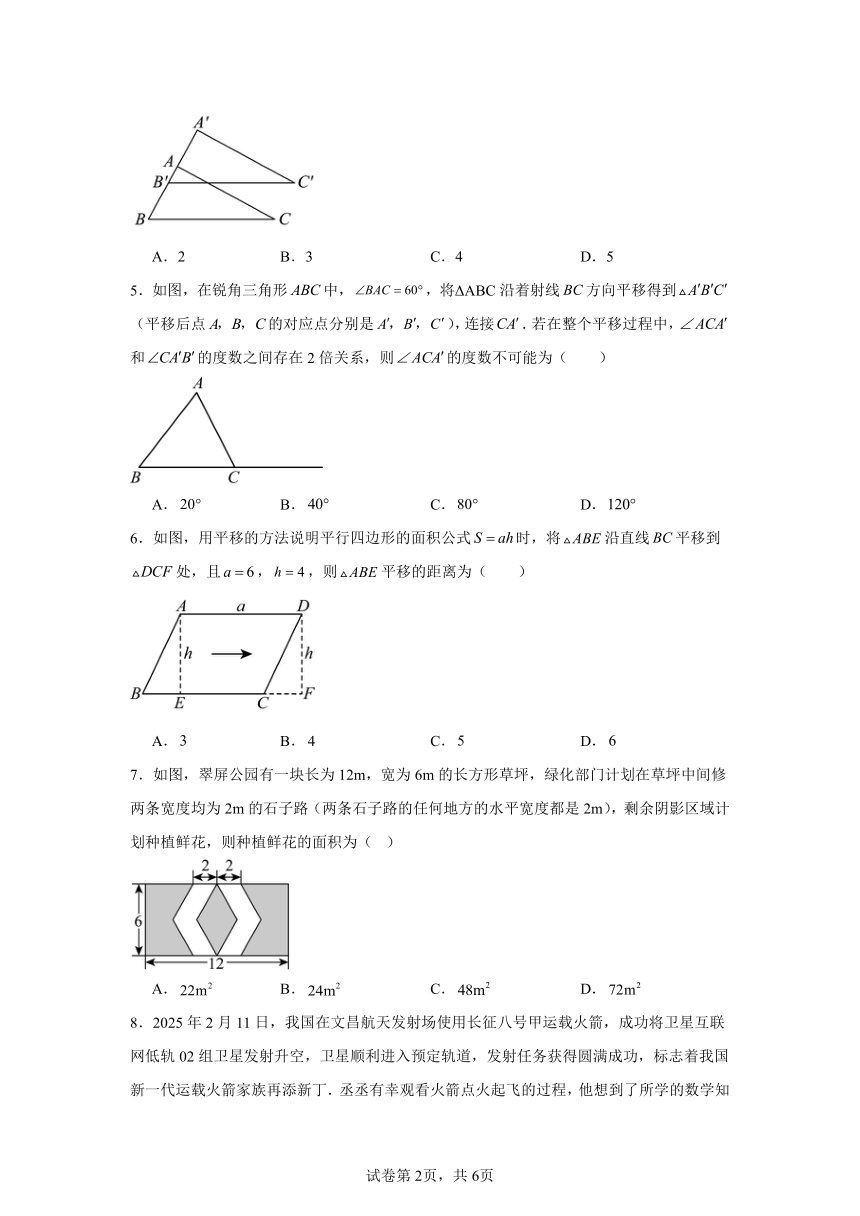
5．如图，在锐角三角形中，，将ΔABC沿着射线方向平移得到（平移后点的对应点分别是），连接．若在整个平移过程中，和的度数之间存在2倍关系，则的度数不可能为（　　）
A． B． C． D．
6．如图，用平移的方法说明平行四边形的面积公式时，将沿直线平移到处，且，，则平移的距离为（　　）
A． B． C． D．
7．如图，翠屏公园有一块长为12m，宽为6m的长方形草坪，绿化部门计划在草坪中间修两条宽度均为2m的石子路（两条石子路的任何地方的水平宽度都是2m），剩余阴影区域计划种植鲜花，则种植鲜花的面积为（ ）
A． B． C． D．
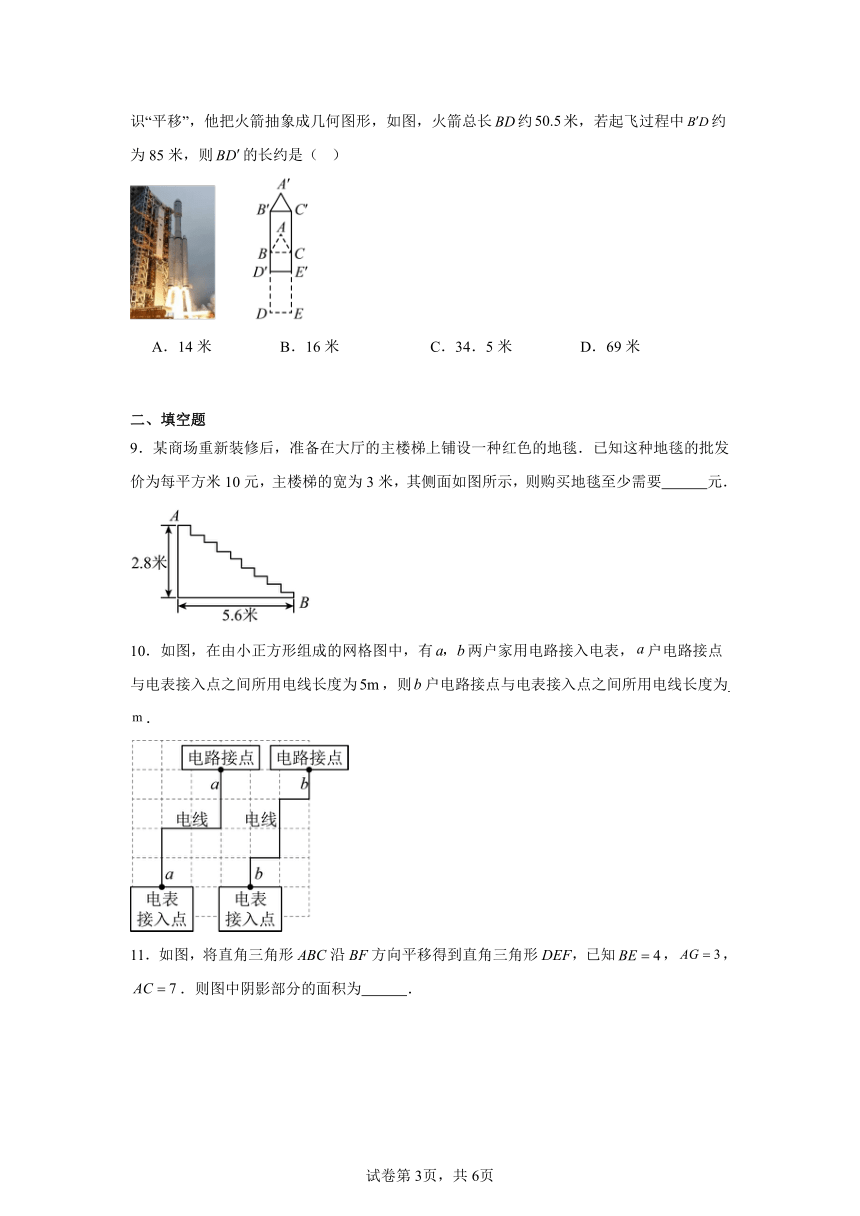
8．2025年2月11日，我国在文昌航天发射场使用长征八号甲运载火箭，成功将卫星互联网低轨02组卫星发射升空，卫星顺利进入预定轨道，发射任务获得圆满成功，标志着我国新一代运载火箭家族再添新丁．丞丞有幸观看火箭点火起飞的过程，他想到了所学的数学知识“平移”，他把火箭抽象成几何图形，如图，火箭总长约米，若起飞过程中约为85米，则的长约是（ ）
A．14米 B．16米 C．34．5米 D．69米
二、填空题
9．某商场重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯．已知这种地毯的批发价为每平方米10元，主楼梯的宽为3米，其侧面如图所示，则购买地毯至少需要 元．
10．如图，在由小正方形组成的网格图中，有两户家用电路接入电表，户电路接点与电表接入点之间所用电线长度为，则户电路接点与电表接入点之间所用电线长度为 ．
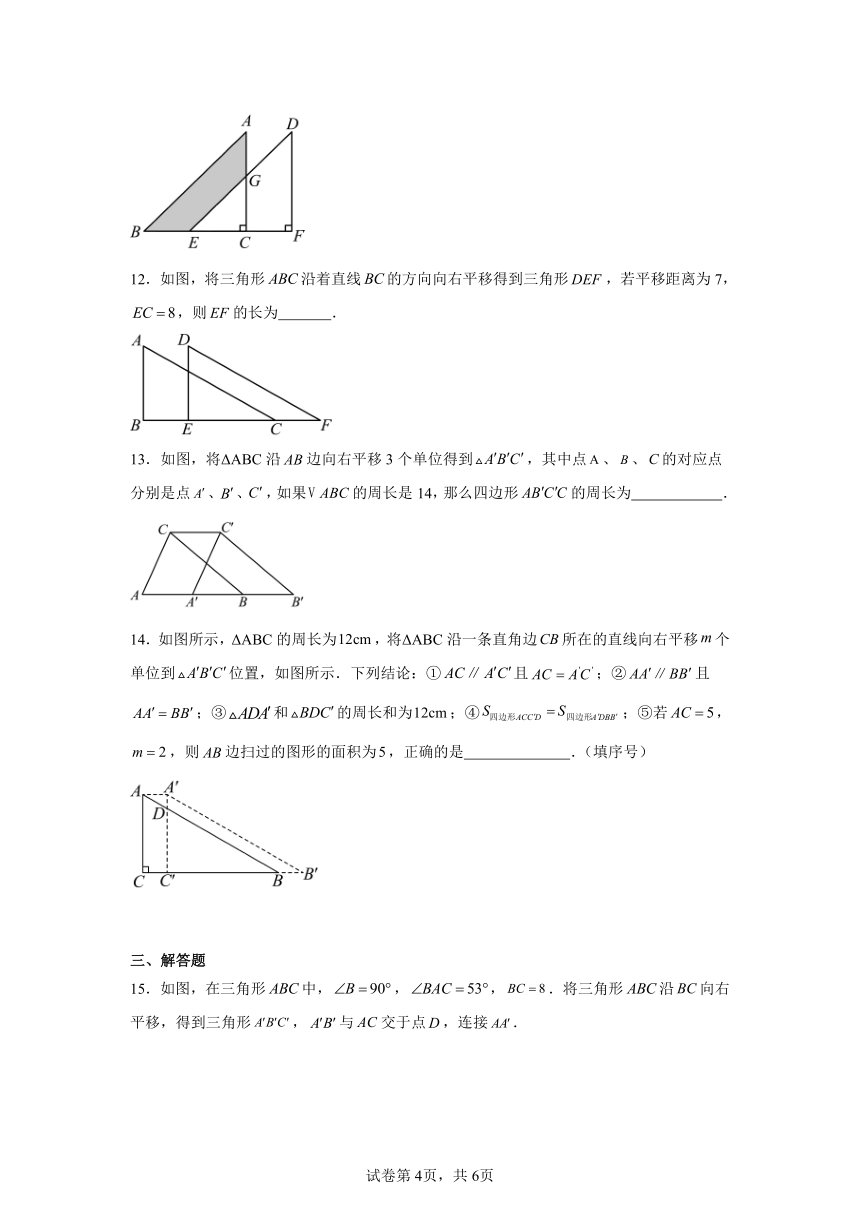
11．如图，将直角三角形ABC沿BF方向平移得到直角三角形DEF，已知，，．则图中阴影部分的面积为 ．
12．如图，将三角形沿着直线的方向向右平移得到三角形，若平移距离为7，，则的长为 ．
13．如图，将ΔABC沿边向右平移3个单位得到，其中点、、的对应点分别是点、、，如果的周长是14，那么四边形的周长为 ．
14．如图所示，ΔABC的周长为，将ΔABC沿一条直角边所在的直线向右平移个单位到位置，如图所示．下列结论：①且；②且；③和的周长和为；④；⑤若，，则边扫过的图形的面积为，正确的是 ．（填序号）
三、解答题
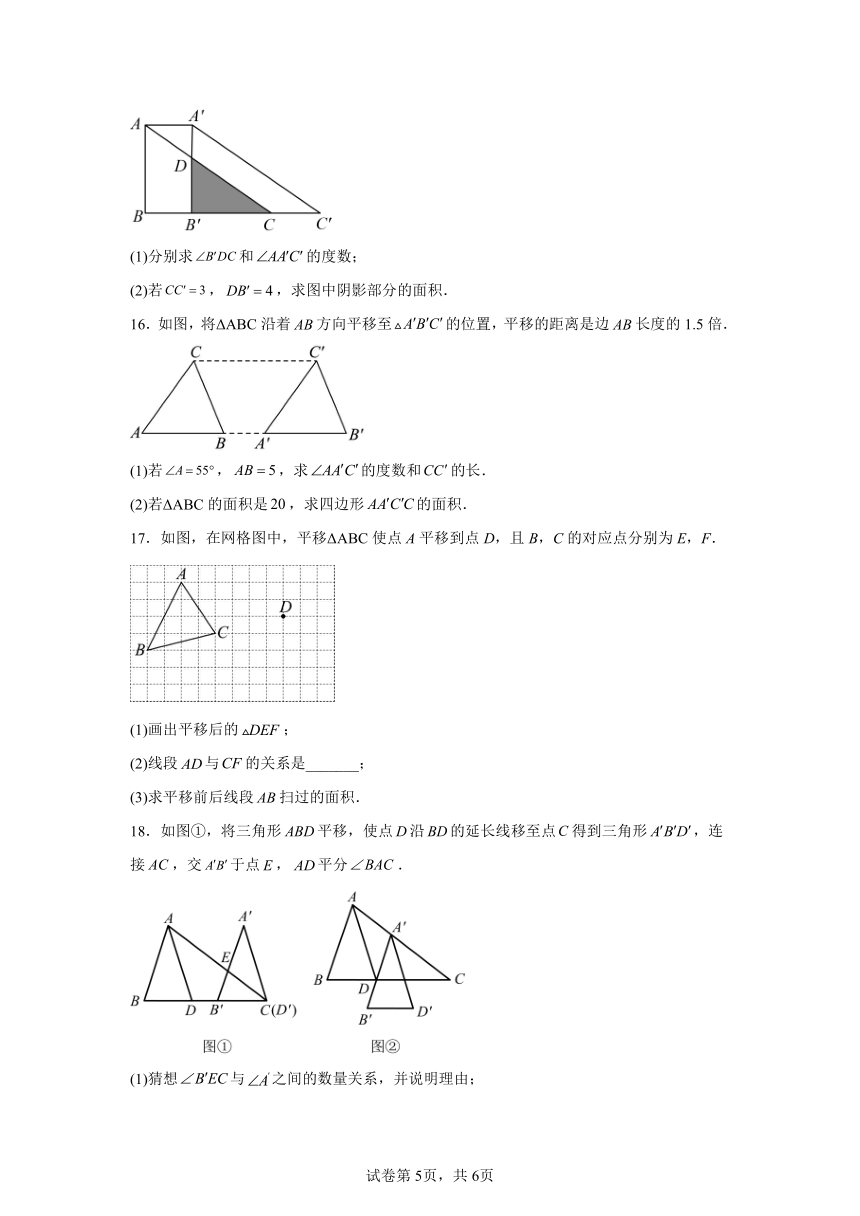
15．如图，在三角形中，，，．将三角形沿向右平移，得到三角形，与交于点，连接．
(1)分别求和的度数；
(2)若，，求图中阴影部分的面积．
16．如图，将ΔABC沿着方向平移至的位置，平移的距离是边长度的1.5倍．
(1)若，，求的度数和的长．
(2)若ΔABC的面积是，求四边形的面积．
17．如图，在网格图中，平移ΔABC使点A平移到点D，且B，C的对应点分别为E，F．
(1)画出平移后的；
(2)线段与的关系是_______；
(3)求平移前后线段扫过的面积．
18．如图①，将三角形平移，使点沿的延长线移至点得到三角形，连接，交于点，平分．
(1)猜想与之间的数量关系，并说明理由；
(2)如图②，将三角形平移，使点A沿移至点得到三角形．如果平分，那么平分吗？为什么？
19．在正方形网格中，每个小正方形的边长均为1个单位长度，ΔABC的顶点位置如图所示．
(1)将ΔABC先向右平移5个单位，再向下平移3个单位，使点A变换为点D，点E、F分别是B、C的对应点，请画出平移后的；
(2)若连接，则这两条线段之间的数量关系是 ，位置关系是 ；
(3)如果点P是线段的中点，画出平移后点P的对应点Q的位置．（利用网格点和直尺画图）．
20．如图，在三角形中，，，．将三角形沿向右平移，得到三角形，与交于点，连接．
(1)________，________；
(2)若，，求图中阴影部分的面积；
(3)已知点在三角形的内部，点经过相同平移后的对应点为，连接．若三角形的周长为，四边形的周长为，请直接写出的长度．
试卷第1页，共3页
试卷第1页，共3页
《七年级数学下册新人教版第七章第4节《平移》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B B A C D C B
9．252
10．
11．22
12．15
13．20
14．①②③④
15．(1)；
(2)10
16．（1）解：ΔABC沿着方向平移至，
．
，
．
平移的距离是边的1.5倍，
．
．
（2）解：作平行交于点D．
ΔABC沿着方向平移至，
，．
、与平行四边形等高，．
．
平移的距离是边的倍，
．
设ΔABC的高为h，
，，
平行四边形的面积三角形的面积，
四边形的面积为．
17．（1）解：如图即为平移后的；
（2）解：线段与的关系是：，．
故答案为：，．
（3）解：如图：
线段扫过的面积为：
．
18．（1）解：．理由如下：
平分，
∴，
由平移的性质，得，，
∴，
（2）解：平分．
理由如下：
由平移的性质，得，，
∴，
平分，
，
∴，即平分．
19．（1）解：如图，即为所求，
（2）解：由平移的性质可知，，．
故答案为：，．
（3）解：如图，线段是所在矩形的对角线，
∴作出线段是所在矩形的另一对角线，两对角线的交点即为的中点，
∴点Q即为所求．
20．（1）解：由平移得，
，
，
，
，
，
，
故答案为：，；
（2）解：由平移得，
；
（3）解：由平移得
，，
，，
，
，
，
，
解得：，
．
答案第1页，共2页
答案第1页，共2页

展开更多......

收起↑