资源简介

平行线性质判定专项训练提升题2
一、解答题
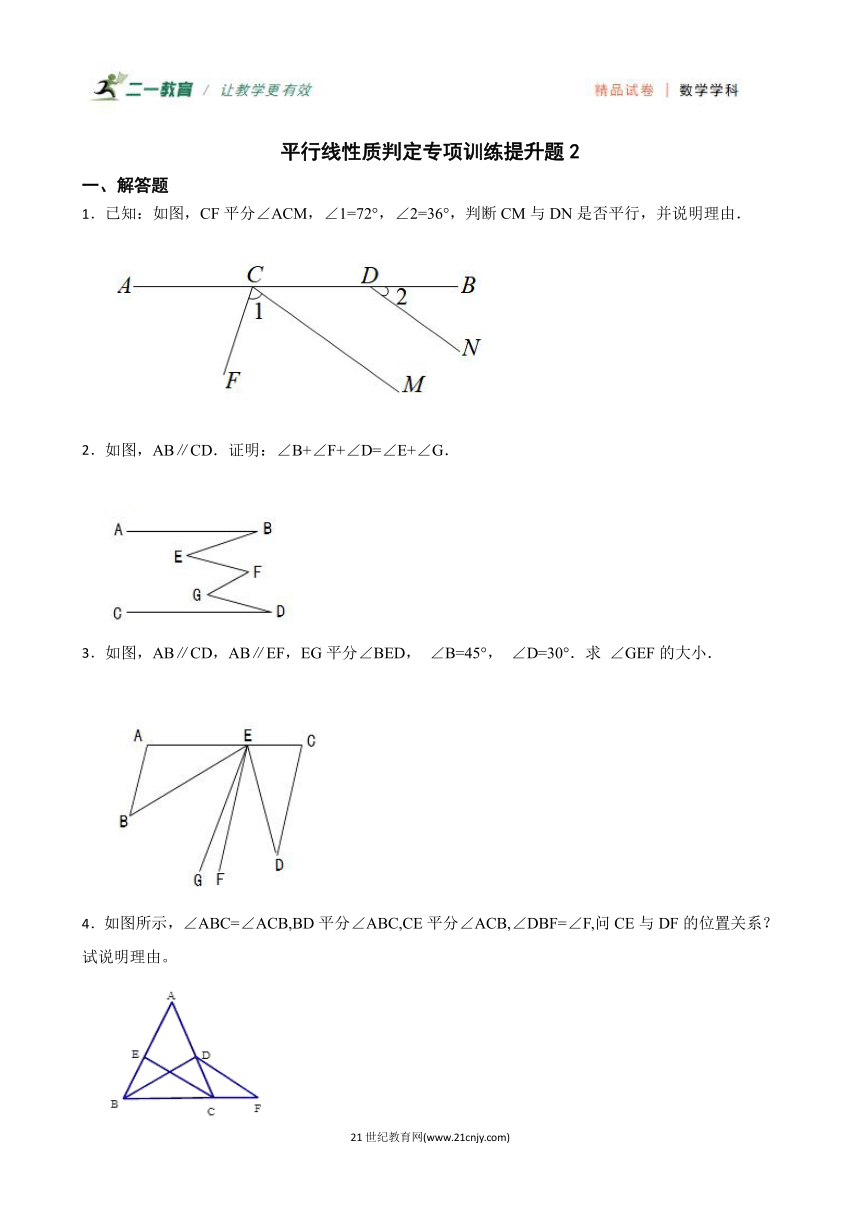
1．已知：如图，CF平分∠ACM，∠1=72°，∠2=36°，判断CM与DN是否平行，并说明理由．
2．如图，AB∥CD．证明：∠B+∠F+∠D=∠E+∠G．
3．如图，AB∥CD，AB∥EF，EG平分∠BED， ∠B=45°， ∠D=30°．求 ∠GEF的大小．
4．如图所示，∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,问CE与DF的位置关系？试说明理由。
二、综合题
5．已知射线（M，N在射线CA的右侧），点B在射线AM上，点D在射线CN上，点E在射线CA上（不与点A重合），且满足∠BAC＋∠BED＝180°．
（1）如图1，点E在线段AC上．
①若∠BED＝60°，∠ABE＝20°，求∠CDE的度数．
②探究∠CDE与∠AEB的数量关系，并说明理由．
（2）设，，∠AEB与∠EDN的平分线交于点P，请用的代数式表示∠EPD的度数．
6．当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等．例如：在图①，有，．设镜子与的夹角．
（1）如图①，若，判断入射光线与反射光线的位置关系，并说明理由；
（2）如图②，若，设镜子与的夹角（），入射光线与镜面的夹角（），已知入射光线分别从镜面、、反射，反射光线与入射光线平行，请求出与的关系式．
7．如图，直线 // ，点E、F分别是 上的动点（点E在点F的右侧），点M为线段 上的一点，点N为射线 上的一点，连接 ．
（1）如图1，若 ，求 的度数．
（2）如图2，作 的角平分线 ，且 // ．求 与 之间的数量关系；
（3）在（2）的条件下，连接 ．且 恰好平分 ，求 的度数．
8．如图1，AB∥CD，，，求的度数．
小明的思路是：过作，通过平行线性质来求．
（1）按小明的思路，求的度数；
（2）（问题迁移）
如图2，，点在射线上运动，记，，当点在、两点之间运动时，问与、之间有何数量关系？请说明理由；
（3）（问题应用）
在（2）的条件下，如果点在、两点外侧运动时（点与点、、三点不重合），请直接写出与、之间的数量关系（并画出相应的图形）．
9．已知直线，动点C在与之间．
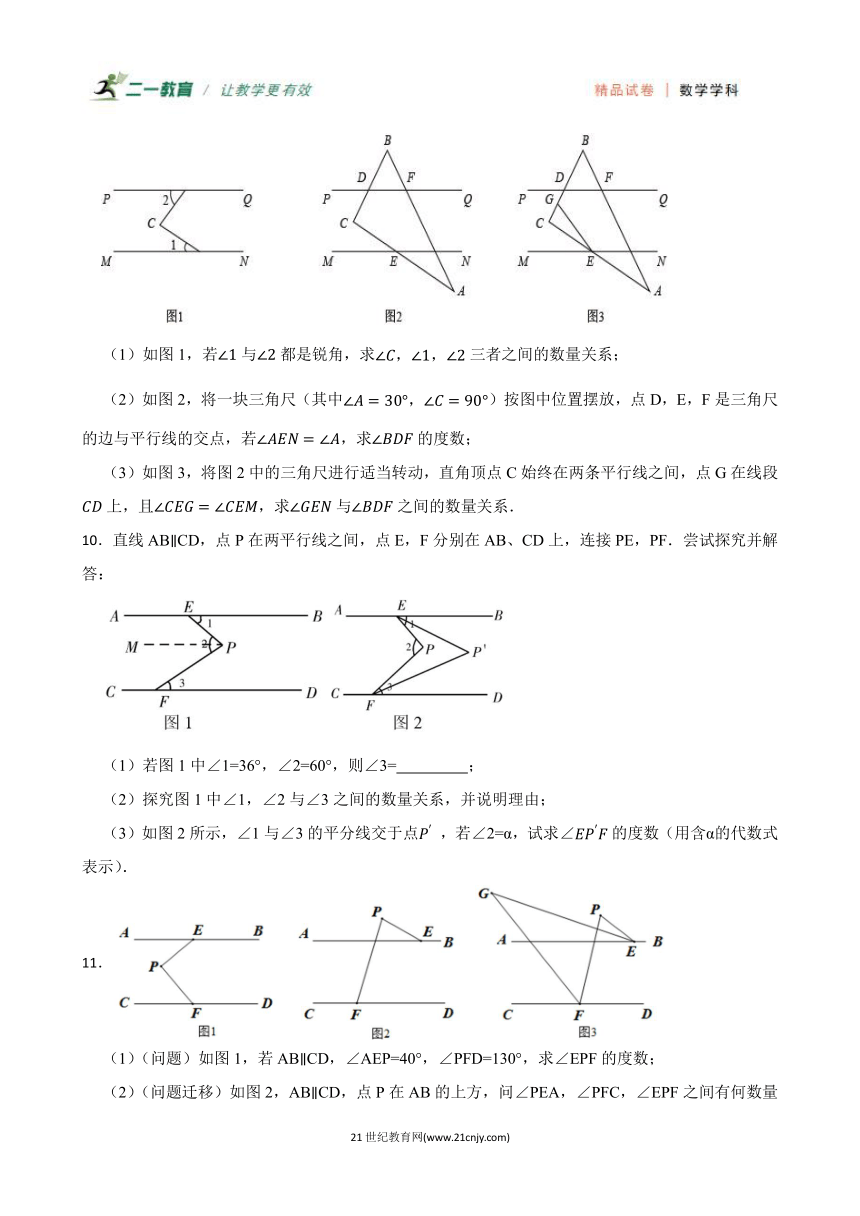
（1）如图1，若与都是锐角，求三者之间的数量关系；
（2）如图2，将一块三角尺（其中）按图中位置摆放，点D，E，F是三角尺的边与平行线的交点，若，求的度数；
（3）如图3，将图2中的三角尺进行适当转动，直角顶点C始终在两条平行线之间，点G在线段上，且，求与之间的数量关系．
10．直线ABCD，点P在两平行线之间，点E，F分别在AB、CD上，连接PE，PF．尝试探究并解答：
（1）若图1中∠1=36°，∠2=60°，则∠3=　 　；
（2）探究图1中∠1，∠2与∠3之间的数量关系，并说明理由；
（3）如图2所示，∠1与∠3的平分线交于点 ，若∠2=α，试求∠的度数（用含α的代数式表示）．
11．
（1）（问题）如图1，若ABCD，∠AEP=40°，∠PFD=130°，求∠EPF的度数；
（2）（问题迁移）如图2，ABCD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；
（3）（问题拓展）如图3所示，在⑵的条件下，已知∠EPF=α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．
12．如图
（1）如图1， ，求 的度数；
（2）如图2， ，点P在射线 上运动，记 ，当点P在B，D两点之间运动时，请写出 与 之间的数量关系，并说明理由；
（3）在（2）的条件下，如果点P在B，D两点外侧运动时（点P与点O，B，D三点不重合），请直接写出 与 之间的数量关系．
13．
（1）如图1，ABCD，，．求 度数．
（2）如图2，ADBC，点在射线 上运动，当点在A、B两点之间运动时，，．． 、、之间有何数量关系？请说明理由．
（3）在（2）的条件下，如果点在A、B两点外侧运动时（点与点A、B、O三点不重合），请你直接写出、、间的数量关系．
14．三角板是学习数学的重要工具 ，将一副三角板的直角顶点 C 按如图所示的方式叠放在一起， 当 时 ，且点 E 在直线AC 的上方时， 解决下列问题∶ （友情提示 ∶ ∠A=60°，∠D=30°，∠B=∠E=45°）
（1）①若 ∠DCE=45°，求∠ACB；
②若∠ACB=140°，求∠DCE ；
（2）由（1）猜想 ∠ACB与∠DCE的数量关系，并说明理由；
（3）这两块三角板是否存在一组边互相平行？
若存在，请直接写出∠ACE的所有可能的值（不必说明理由）；若不存在，请说明理由．
15．在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG(∠EFG=90°，∠EGF=60°)”为主题开展数学活动.
（1）如图1，若三角尺的60°角的顶点放在CD上，若，求∠1的度数；
（2）如图2，小颓把三角尺的两个锐角的顶点E，G分别放在AB和CD上，请你探索并说明与间的数量关系；
（3）如图3，小亮把三角尺的直角顶点放在CD上，角的顶点落在AB上.若，则与的数量关系是什么 用含的式子表示并说明理由.
16．如图，，是与之间的一点，是上的任意一点，且.
（1）求证：平分；
（2）过点作直线于.
①如备用图，若，过点作的平分线交于点，求证：；
②如备用图，过点，分别作，的平分线相交于点，设，求的值.（用含的式子表示）
17．在平面直角坐标系中，D（0，﹣3），M（4，﹣3），直角三角形ABC的边与x轴分别相交于O、G两点，与直线DM分别交于E、F点，∠ACB＝90°.
（1）将直角三角形如图1位置摆放，如果∠AOG＝46°，则∠CEF＝　 　；
（2）将直角三角形ABC如图2位置摆放，N为AC上一点，∠NED+∠CEF＝180°，请写出∠NEF与∠AOG之间的等量关系，并说明理由.
（3）将直角三角形ABC如图3位置摆放，若∠GOC＝140°，延长AC交DM于点Q，点P是射线GF上一动点，探究∠POQ，∠OPQ与∠PQF的数量关系，请直接写出结论（题中的所有角都大于0°小于180°）.
答案解析部分
1．【答案】解：CM∥DN
∵CF平分∠ACM
∴∠ACM=2∠1
∵∠1=72°
∴∠ACM=2∠1=144°
∴∠BCM=180°-144°=36°
∵∠2=36°，
∴∠2 =∠BCM．
∴CM∥DN
【解析】【分析】根据角平分线的定义可得∠ACM=2∠1，则∠ACM=2∠1=144°，∠BCM=180°-144°=36°，可得∠2 =∠BCM，则CM∥DN。
2．【答案】证明：作EM∥AB，FN∥AB，GK∥AB，
∵AB∥CD，
∴AB∥ME∥FN∥GK∥CD，
∴∠B=∠1，∠2=∠3，∠4=∠5，∠6=∠D，
∴∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6，
又∵∠E+ ∠G=∠1+∠2+∠5+∠6，
∠B+ ∠F+ ∠D=∠B+ ∠3+∠4+ ∠D，
∴∠B+ ∠F+ ∠D=∠E+ ∠G.
【解析】【分析】作EM∥AB，FN∥AB，GK∥AB，根据平行公理及推论可得AB∥ME∥FN∥GK∥CD，再由平行线性质得∠B=∠1，∠2=∠3，∠4=∠5，∠6=∠D，相加即可得证.
3．【答案】解：因为AB∥CD，AB∥EF，所以EF∥CD，所以内错角 FED= D=30°．又因为AB∥EF，所以内错角FEB=B=45°，从而， BED=FED+FEB=75°．因为EG平分BED，所以BEG= BED=37.5°．从而 GEF=BEF-BEG=45°-37.5°=7.5°．所以 GEF为7.5°．
【解析】【分析】根据平行线的性质得∠FED=∠D=30°，∠FEB=∠B=45°，从而得∠BED=75°；再由角平分线性质得∠BEG=37.5°，由∠GEF=∠BEF- ∠BEG即可求得答案.
4．【答案】.CE∥DF.
∵BD平分∠ABC,CE平分∠ACB,
∴∠DBF=1／2∠ABC, ∠ECB=1／2∠ACB,
∵∠ABC=∠ACB,
∴∠DBF=∠ECB.
∵∠DBF=∠F,
∴∠ECB=∠F. ∠CE∥DF（同位角相等，两直线平行).
【解析】【解答】∵BD平分∠ABC,CE平分∠ACB,
∴∠DBF=1／2∠ABC, ∠ECB=1／2∠ACB,
∵∠ABC=∠ACB,
∴∠DBF=∠ECB.
∵∠DBF=∠F,
∴∠ECB=∠F. ∠CE∥DF同位角相等，两直线平行).
【分析】要证平行可寻找题目中有没有同位角或内错角或同旁内角，然后学会等量代换，推理论证。
5．【答案】（1）解：①如图1所示：过点E作
②在中，
（2）解：如图2所示：
由（1）可知
∵EP平分，DP平分
在中，
即
，
【解析】【分析】（1）①过点E作EF∥AM，根据平行于同一直线的两条直线互相平行得AM∥EF∥CN，从而根据平行线的性质（两直线平行，内错角相等）可得出∠ABE+∠CDE=∠BED，代入即可求出结果；
②在△AEB中，由三角形的内角和定理（三角形的内角和等于180°）得∠BAE+∠AEB+∠ABE=180°，再根据已知条件∠BAC+∠BED=180°，从而可得出∠ABE+∠CDE=∠BED，即可得出结果；
（2）根据已知条件可得出∠AEB+∠EDN=180°，在△AEB中，根据三角形内角和定理（三角形的内角和等于180°）得到∠BAE+∠AEB+∠ABE=180°，再根据角平分线得∠BEP+∠EDP=90°，从而得到∠BED+∠EPD=90°，即可得出结果.
6．【答案】（1）解：EF∥GH，
理由：在△BEG中，∠2＋∠3＋α＝180°，α＝90°，
∴∠2＋∠3＝90°，
∵∠1＝∠2，∠3＝∠4，
∴∠1＋∠2＋∠3＋∠4＝180°，
∵∠1＋∠2＋∠FEG＝180°，∠3＋∠4＋∠EGH＝180°，
∴∠FEG＋∠EGH＝180°，
∴EF∥GH；
（2）解：，
理由：如图，作GM∥EF，
∵EF∥HK，
∴GM∥HK，
∵∠1＝∠2，∠1＝β，
∴∠2＝β，
∴∠FEG＝180°－2β，
∴∠EGM＝180°－（180°－2β）＝2β，
在△BEG中，∠2＋∠3＋α＝180°，，
∴∠3＝180°－135°－∠2＝45°－β，
∴∠3＝∠CGH＝45°－β，
∴∠MGH＝180°－∠3－∠EGM－∠CGH＝180°－2（45°－β）－2β＝90°，
∵GM∥HK，
∴∠MGH＋∠GHK＝180°，
∴∠GHK＝90°，
∵∠GHC＝∠KHD，∠GHK＝180°－∠GHC－∠KHD＝90°，
∴∠GHC＝∠KHD＝45°，
∴∠BCD＝180°－∠CGH－∠CHG＝180°－（45°－β）－45°＝90°＋β，即．
【解析】【分析】（1）在△BEG中，∠2+∠3＋α=180°，α=90°，可得∠2+∠3=90°，根据入射光线、反射光线与镜面所夹的角对应相等可得 ∠FEG＋∠EGH＝180° ，进而根据“同旁内角互补两直线平行”可得 EF∥GH ；
（2） 作GM∥EF ，根据平行于同一直线的两条直线互相平行，得GM∥HK ，结合已知条件和平行线的性质（两直线平行，同旁内角互补）可证 ∠EGM＝180°－（180°－2β）＝2β ，利用△BEG内角和及已知条件可得 ∠3＝∠CGH＝45°－β ，进一步求出 ∠MGH＝90° ，再利用平行线的性质（两直线平行，同旁内角互补）和入射光线、反射光线与镜面所夹的角对应相等可得 .
7．【答案】（1）解：如图1： ， ，
，
，
，
，
（2）解：如图2，
，
，
， ，
是 的角平分线，
，
；
（3）解： ，
，
平分 ，
，
，
， ，
∴∠AEF＝2∠ENM，∠BEN=∠FEN=3∠ENM
，
解得 ，
．
【解析】【分析】（1）根据平行线的性质可得∠BEF+∠DFE=180°，结合∠BEF的度数可得∠DFE的度数，根据垂直的概念可得∠FMN=90°，然后根据∠MNF=90°-∠DFE进行计算；
（2）根据平行公理及推论得AB∥CD∥MQ，由平行线的性质得∠MNF=∠NMQ，∠EMQ=∠AEF，根据角平分线的概念可得∠NMQ=∠EMQ，据此解答；
（3）根据平行线的性质得∠ENF=∠BEN，根据角平分线的概念得∠BEN=∠FEN，则∠ENF=∠FEN，结合已知条件可得∠AEF＝2∠ENM，∠BEN=∠FEN=3∠ENM，求出∠ENM的度数，进而可得∠EMN的度数.
8．【答案】（1）解：过点P作PE∥AB，
∵AB∥CD，
∴PE∥AB∥CD，
∴∠A+∠APE＝180°，∠C+∠CPE＝180°，
∵∠PAB＝130°，∠PCD＝120°，
∴∠APE＝50°，∠CPE＝60°，
∴∠APC＝∠APE+∠CPE＝110°．
（2）解：∠APC＝α+β，
理由：如图2，过P作PE∥AB交AC于E，
∵AB∥CD，
∴AB∥PE∥CD，
∴α＝∠APE，β＝∠CPE，
∴∠APC＝∠APE+∠CPE＝α+β；
（3）解：如图所示，当P在BD延长线上时，
过点P作PE∥CD交ON于E，则PE∥AB，
∴∠APE=α，∠CPE=β，
∴∠CPA=∠APE-∠CPE=α-β；
如图所示，当P在DB延长线上时，
过点P作PE∥CD交ON于E，则PE∥AB，
∴∠CPE=β，∠APE=α，
∴∠CPA=∠CPE-∠APE=β-α．
【解析】【分析】（1）过点P作PE∥AB，根据平行于同一直线的两条直线互相平行得PE∥AB∥CD，根据二直线平行，同旁内角互补，得∠A+∠APE＝180°，∠C+∠CPE＝180°，据此求出∠APE、∠CPE的度数，然后根据∠APC＝∠APE+∠CPE进行计算；
（2）过P作PE∥AB交AC于E，根据平行于同一直线的两条直线互相平行得 AB∥PE∥CD，根据二直线平行，内错角相等，得α＝∠APE，β＝∠CPE，然后根据∠APC＝∠APE+∠CPE进行计算；
（3）当P在BD延长线上时，过点P作PE∥CD交ON于E，则PE∥AB，根据二直线平行，内错角相等，得∠APE=α，∠CPE=β，然后根据∠CPA=∠APE-∠CPE进行计算； 当P在DB延长线上时，同理解答即可.
9．【答案】（1）解：，
理由：如图，过C作，
∵，
∴，
∴，，
∴，
∴；
（2）解：∵∠MEC=∠AEN，又∠AEN＝∠A，
∴∠MEC=∠A=30°，
由（1）可知：∠C=∠PDC+∠MEC，
又∵∠C＝90°，
∴∠PDC=90°-30°=60°，
则∠BDF=∠PDC=60°；
（3）解：设，则，
由（1）可得，，
∴，
∴，
∴．
【解析】【分析】（1）过C作CD∥PQ，则PQ∥CD∥MN，根据平行线的性质可得∠1=∠ACD，∠2=∠BCD，然后根据∠ACB=∠ACD+∠BCD进行解答；
（2）由对顶角的性质可得∠MEC=∠AEN，结合∠AEN＝∠A，得∠MEC=∠A=30°，由（1）可知∠C=∠PDC+∠MEC，据此可求出∠PDC的度数，然后根据对顶角的性质进行解答；
（3）设∠CEG=∠CEM=x，根据平角的概念得∠GEN=2(90°-x)，由（1）得∠C=∠CEM+∠CDP，则∠CDP=90°-x，由对顶角的性质可得∠BDF=∠CDP=90°-x，据此解答.
10．【答案】（1）24°
（2）解：结论：∠2=∠1+∠3．
理由：如图1中，作PMAB．
∵ABCD，ABPM，
∴PMCD，
∴∠1=∠MPE，∠3=∠MPF，
∴∠2=∠1+∠3．
（3）解：如图2中，
∵∠BEP+∠DFP=∠2=α，
∴∠=∠+∠=（∠BEP+∠DFP）=α
【解析】【解答】解：（1）过点P作PM∥AB．
∵AB∥CD，AB∥PM，
∴PM∥CD，
∴∠1=∠MPE=36°，∠3=∠MPF，
∴∠3=∠2-∠1=60°-36°=24°．
故答案为：24°.
【分析】（1）作PM∥AB，根据平行于同一直线的两条直线互相平行得AB∥CD∥PM， 根据平行线的性质可得∠1=∠MPE，∠3=∠MPF，然后根据∠3=∠2-∠1进行计算；
（2）作PM∥AB，根据平行于同一直线的两条直线互相平行得AB∥CD∥PM， 根据平行线的性质可得∠1=∠MPE，∠3=∠MPF，然后根据∠2=∠1+∠3进行计算；
（3）易得∠BEP+∠DFP=∠2=α，然后根据∠EP′F=∠BEP′+∠DFP′结合角平分线的概念进行计算.
11．【答案】（1）解：过P点作PH//CD
可得：∠1+∠PFD=180°
∵∠PFD=130°
∴∠1=50°
又∵AB//CD
∴PH//AB
可得：∠2=∠AEP=40°
故：∠EPF=∠1+∠2=90°
（2）解：∠PFC=∠PEA+∠EPF
理由：如图2，过点P作PH//AB
可得：∠1=∠PEA
∵AB//CD
∴PH//CD
可知：∠PFC=∠HPF
由于∠HPF=∠1+∠EPF
∴∠PFC=∠1+∠EPF
即：∠PFC=∠PEA+∠EPF
（3）解：令AB与PF的交点为O，连接EF，如图3
在△GFE中，∠G=180°-（∠GFE+∠GEF）
∵∠GEF=∠PEA+∠OEF
∠GFE=∠PFC+∠OFE
∴∠GEF+∠GFE=∠PEA+∠PFC+∠OEF+∠OFE
由（2）可知∠PFC=∠PEA+∠EPF
∴∠PEA=∠PFC-α
又∵AB//CD
可得：∠EOF=∠PFC
∴在△OEF中有：
∠OFE+∠OEF=180°-∠FOE=180°-∠PFC
则∠GEF+∠GFE=（∠PFC-α）+∠PFC+180°-∠PFC
=180°-α
∴∠G=180°-（∠GEF+∠GFE）
=180°-（180°-α）
=α
【解析】【分析】（1）过点P作PH∥CD，根据平行于同一直线的两条直线互相平行得AB∥CD∥PH，由平行线的性质得∠1+∠PFD=180°，∠2=∠AEP=40°，然后根据∠EPF=∠1+∠2进行计算；
（2）过点P作PH//AB，根据平行于同一直线的两条直线互相平行得AB//CD∥PH，由平行线的性质可得∠1=∠PEA，∠PFC=∠HPF，则∠PFC=∠HPF=∠1+∠EPF，据此解答；
（3）令AB与PF的交点为O，连接EF，由内角和定理可得∠G=180°-(∠GFE+∠GEF)，结合角平分线的概念可得∠GEF+∠GFE=∠PEA+∠PFC+∠OEF+∠OFE，由（2）可知∠PFC=∠PEA+∠EPF，则∠PEA=∠PFC-α，根据平行线的性质可得∠EOF=∠PFC，结合内角和定理可得∠GEF+∠GFE=（∠PFC-α）+∠PFC+180°-∠PFC=180°-α，据此计算.
12．【答案】（1）解：如图，过P作PE∥AB，
∵AB∥CD，
∴AB∥PE∥CD，
∴∠APE=180°-∠PAB=50°，∠CPE=180°-∠PCD=60°，
∴；
（2）解： ，理由如下：
如图，过P作PE∥AB，
∵AB∥CD，
∴AB∥PE∥CD，
∴∠APE=∠PAB=α，∠CPE=∠PCD=β，
∴；
（3）解：∠APC =α-β或∠APC =β-α，理由如下：
①如图，当点P在BD的延长线上时，过P作PE∥AB，
∴AB∥PE∥CD，
∴∠APE=∠PAB=α，∠CPE=∠PCD=β，
∴∠APC =α-β；
②如图，当点P在DB的延长线上时，过P作PE∥AB，
∴AB∥PE∥CD，
∴∠APE=∠PAB=α，∠CPE=∠PCD=β，
∴∠APC =β-α；
综上所述，∠APC =α-β或∠APC =β-α.
【解析】【分析】(1)过点P作PE∥AB，得出AB∥PE∥CD，先根据平行线的性质求出∠APE和∠CPE的度数，最后根据角的和差即可求出结果；
(2)过点P作PE∥AB，根据平行公理推论可得PE∥CD，再根据平行线的性质得出∠APE=∠PAB=a，∠CPE=∠PCD= β，再根据角的和差，即可得出结论；
(3)分①点P在BD的延长线上和②点P在DB的延长线上两种情况讨论，根据(1) 和(2) 的方法作辅助线，利用平行线的性质和平行公理推论，即可求出结论.
13．【答案】（1）解：如图1：过P作PMCD，
，
∴，
又∵ABCD，∴PMAB，
∴，
∴，
∴．
（2）解：，理由如下：
如图2，过点P作PEAD，交CD于点E，连接PE，则PEBC，
∴，，
∴
∴
即．
（3）解：①当P在射线AM上时，；
②当P在点O与点B之间时，．
理由：①当P在射线AM上时，如图3，
过点P作PFAD，交射线ON于点F，连接PF，则PFBC，
∴，，
∴，
∴，
即．
②当P在点O与点B之间时，如图4，过点P作PGAD，交OD于点G，连接PG，则PGBC，
∴，，
∴，
∴
即．
【解析】【分析】（1） 过P作PM∥CD，由两直线平行同旁内角互补可求∠MPC的度数，由平行线的传递性得PM∥CD∥AB，由两直线平行同旁内角互补可求∠MPA的度数，然后由∠APC=∠APM+∠MPC可求解；
（2）过点P作PE∥AD，交CD于点E，连接PE，则PE∥BC，由两直线平行内错角相等，可得∠ADP=∠EPD，∠BCP=∠EPC，再由角的构成∠DPC=∠EPD+∠EPC=∠ADP+∠BCP可求解；
（3）由题意可分两种情况：①当P在射线AM上时，过点P作PF∥AD，交射线ON于点F，连接PF，则PF∥BC，由两直线平行内错角相等可得∠DPfF=∠PDA，∠BCP=∠FPC，再由角的构成可求解；②当P在点O与点B之间时，如图4，过点P作PG∥AD，交OD于点G，连接PG，则PG∥BC， 同理可求解.
14．【答案】（1）解：①∵∠ACD=90°，∠DCE=45°，
∴∠ACE=45°，
∴∠ACB=∠ACE+∠ECB=45°+90°=135°；
②∵∠ACB=140°，∠ACD=∠ECB=90°，
∴∠ACE=140°－90°=50°，
∴∠DCE=∠DCA－∠ACE =90°－50°=40°；
（2）解：∠ACB与∠DCE互补．理由如下：
∵∠ACD=90°，
∴∠ACE=90°－∠DCE，
又∵∠BCE=90°，所以∠ACB=∠BCE+∠ACE =90°+90°－∠DCE=180°－∠DCE，
∴∠ACB+∠DCE=180°－∠DCE+∠DCE=180°；
（3）解：存在一组边互相平行．
当∠ACE=45°时，∠ACE=∠E=45°，
此时AC∥BE，
当∠ACE=30°时，∠ACB=120°，
此时∠A+∠ACB=180°，
此时AD∥BC．
【解析】【分析】（1）①由角的构成得∠ACE=∠ACD-∠DCE可求得∠ACE的度数，再由∠ACB=∠ACE+∠BCE可求解；
②由角的构成得∠ACE=∠ACB-∠BCE可求得∠ACE的度数，然后结合图形得∠DCE=∠ACD-∠ACE可求解；
（2）由∠ACE=∠ACD-∠DCE，∠ACB=∠BCE+∠ACE=180°－∠DCE，于是∠ACB+∠DCE=180°－∠DCE+∠DCE可求解；
（3）存在一组边互相平行，结合题意根据同旁内角互补两直线平行及内错角相等两直线平行可求解.
15．【答案】（1）解：∵AB//CD
∴∠1=∠EGD
∵∠2+∠FGE＋∠EGD=180°，∠2=2∠1
∴2∠1＋60°＋∠1=180°，解得∠1=40°
（2）解：如图，过点F作FP∥AB.
∵CD//AB
∴FP//AB//CD
∴∠AEF=∠EFP、∠FGC=∠GFP
∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG.
∵∠EFG=90°
∴∠AEF+∠FGC=90°
（3）解：
理由如下：
∵AB//CD
∴∠AEF+∠CFE=180°
即
整理得
【解析】【分析】（1）利用两直线平行，同位角相等，可证得∠1=∠EGD；再利用平角的定义可知∠2+∠FGE＋∠EGD=180°，结合已知条件可得到关于∠1的方程，解方程求出∠1的度数.
（2）过点F作FP∥AB，利用同平行于一条直线的两直线平行，可证得FP//AB//CD，利用平行线的性质可推出∠AEF=∠EFP、∠FGC=∠GFP，根据∠EFG=∠EFP+∠PFG，代入可证得∠AEF和∠FGC的关系.
（3）利用平行线的性质可证得∠AEF+∠CFE=180°，可推出α-30°+β-90°=180°，由此可得到α和β的数量关系.
16．【答案】（1）证明：∵，
∴，
∵，
∴，
∴平分.
（2）证明：①设AC与IF交于点O，如图所示：
∵，
∴，，
∵，
∴，
∴，
∵FI平分∠AFE，平分，
∴，，
∴，
∴，
，
∵，
∴；
②过点E作，
∵CK平分∠DCG，FK平分∠BFE，
∴∠DCG=2∠1，∠BFE=2∠2，
∵，
∴，
∴∠3=∠6，∠4=∠EFB，∠2=∠5，
∵CH⊥CE，
∴∠ECG=90°，
∴，
∵，
∴
.
【解析】【分析】（1）根据二直线平行，同旁内角互补可得∠A+∠ACD=180°，结合已知条件可得∠ACD=2∠ACE，据此证明；
（2）①设AC与IF交于点O，根据平行线的性质可得∠A+∠AFE=180°，∠AOF=∠IFE，∠A+∠ACD=180°，推出∠AFE=∠ACD，结合角平分线的概念可得∠IFE=∠ACE，则∠AOF=∠ACE，推出OF∥CE，然后结合CE⊥CH进行证明；
②过点E作EM∥AB，根据角平分线的概念可得∠DCG=2∠1，∠BFE=2∠2，根据平行线的性质可得∠3=∠6，∠4=∠EFB，∠2=∠5，则∠6=90°-2∠1，根据外角的性质可得∠5=∠K+∠1，则∠CEF=∠3+∠4=∠6+∠EFB，据此解答.
17．【答案】（1）136°
（2）解：∠AOG+∠NEF＝90°.
理由如下：如图2，作CP∥x轴，
∵CP∥DM∥x轴，
∴∠AOG＝∠1，∠2+∠CEF＝180°，
而∠NED+∠CEF＝180°，
∴∠2＝∠NED，
∵∠1+∠2＝90°，
∴∠AOG+∠NEF＝90°；
（3）解：如图3，当点P在GF上时，过点P作PN∥OG，
∴NP∥OG∥DM，
∴∠GOP＝∠OPN，∠PQF＝∠NPQ，
∴∠OPQ＝∠GOP+∠PQF，
∴∠OPQ＝140°﹣∠POQ+∠PQF；
如图4，当点P在线段GF的延长线上时，过点P作PN∥OG，
∴NP∥OG∥DM，
∴∠GOP＝∠OPN，∠PQF＝∠NPQ，
∵∠OPN＝∠OPQ+∠QPN，
∴∠GOP＝∠OPQ+∠PQF，
∴140°﹣∠POQ＝∠OPQ+∠PQF.
【解析】【解答】解：（1）如图1，作CP∥x轴，
∵D（0，﹣3），M（4，﹣3），
∴DM∥x轴，
∴CP∥DM∥x轴，
∴∠AOG＝∠1，∠2+∠CEF＝180°，
∴∠2＝180°﹣∠CEF，
∵∠1+∠2＝90°，
∴∠AOG+180°﹣∠CEF＝90°，
∵∠AOG＝46°，
∴∠CEF＝136°.
故答案为：136°；
【分析】（1）作CP∥x轴，根据点M、D的坐标可得DM∥x轴，则CP∥DM∥x轴，根据平行线的性质可得∠AOG＝∠1，∠2+∠CEF＝180°，结合∠1+∠2=180°可得∠AOG+180°-∠CEF＝90°，据此求解；
（2）作CP∥x轴，则CP∥DM∥x轴，根据平行线的性质可得∠AOG＝∠1，∠2+∠CEF＝180°，由已知条件可得∠NED+∠CEF＝180°，则∠2＝∠NED，然后结合∠1+∠2＝90°进行解答；
（3）当点P在GF上时，过点P作PN∥OG，根据平行线的性质可得∠GOP＝∠OPN，∠PQF＝∠NPQ，则∠OPQ＝∠GOP+∠PQF，据此计算；当点P在线段GF的延长线上时，过点P作PN∥OG，根据平行线的性质可得∠GOP＝∠OPN，∠PQF＝∠NPQ，则∠GOP＝∠OPQ+∠PQF，据此计算.
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑