资源简介

2024-2025学年北京市海淀区第二十中学九年级下学期4月中考模拟
数学试卷
一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。
1.年，我国共授权发明专利万件，同比增长将用科学记数法表示应为( )
A. B. C. D.
2.下列几何体放置在水平面上，其中俯视图是三角形的几何体为( )
A. B. C. D.
3.如图，，，则的大小为( )
A. B. C. D.
4.若，则下列结论正确的是( )
A. B. C. D.
5.关于的方程有实数根，那么的可能值是( )
A. B. C. 或 D. 或
6.先后两次抛掷同一枚质地均匀的硬币，则第一次正面向上、第二次反面向上的概率是( )
A. B. C. D.
7.如图，已知，求作：，使．
作法：以点为圆心，任意长为半径作，分别交，于点，，连接；
以为圆心，的长为半径作弧，交于点，连接，；
作射线，即为所求作的角．下列结论正确的是( )
A. 的依据是两边和它们的夹角分别相等的两个三角形全等
B.
C.
D. 是等腰三角形
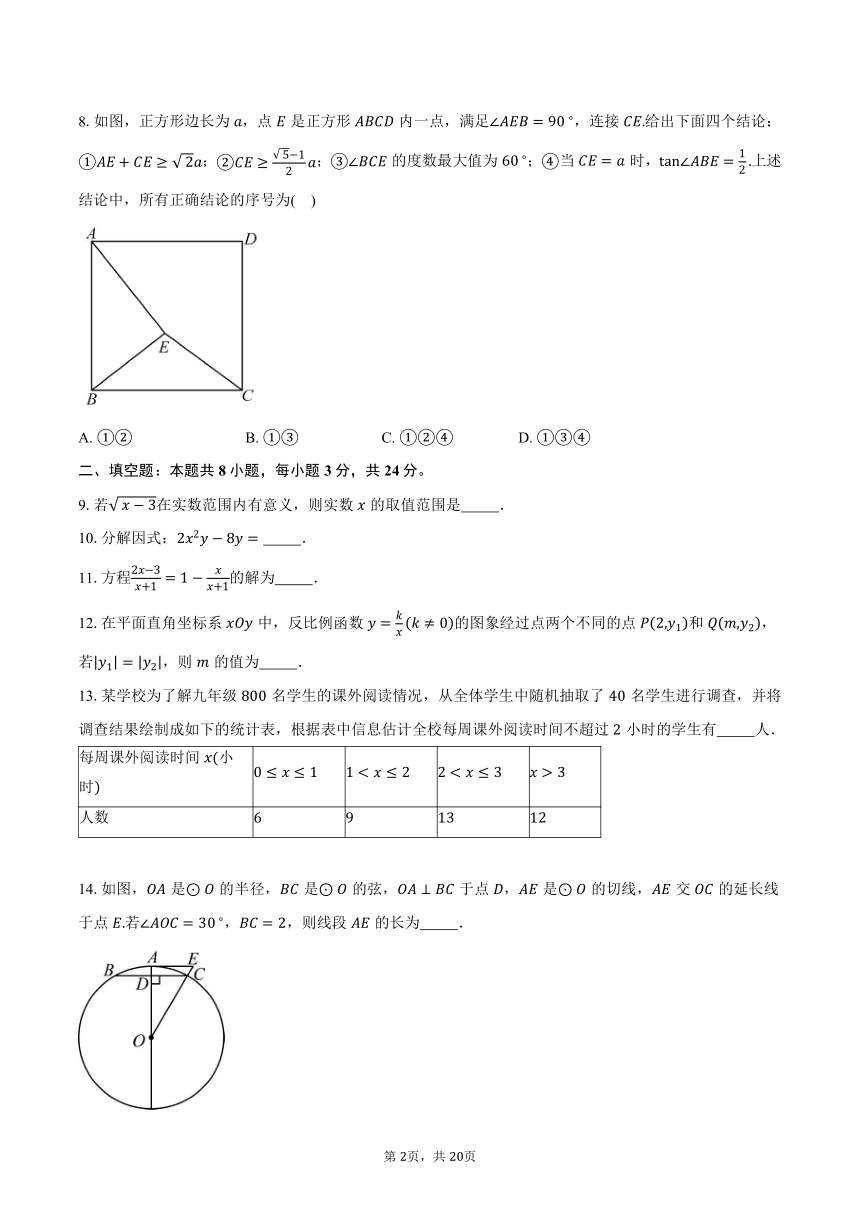
8.如图，正方形边长为，点是正方形内一点，满足，连接给出下面四个结论：；；的度数最大值为；当时，上述结论中，所有正确结论的序号为( )
A. B. C. D.
二、填空题：本题共8小题，每小题3分，共24分。
9.若在实数范围内有意义，则实数的取值范围是 ．
10.分解因式： ．
11.方程的解为 ．
12.在平面直角坐标系中，反比例函数的图象经过点两个不同的点和，若，则的值为 ．
13.某学校为了解九年级名学生的课外阅读情况，从全体学生中随机抽取了名学生进行调查，并将调查结果绘制成如下的统计表，根据表中信息估计全校每周课外阅读时间不超过小时的学生有 人．
每周课外阅读时间小时
人数
14.如图，是的半径，是的弦，于点，是的切线，交的延长线于点若，，则线段的长为 ．
15.如图，在中，点在上，交于点若，则的值为 ．
16.某酒店在客人退房后清洁客房需打扫卫生、整理床铺、更换客用物品、检查设备共四个步骤．某清洁小组有甲、乙、丙三名工作人员，工作要求如下：
“打扫卫生”只能由甲完成；每间客房“打扫卫生”完成后，才能进行该客房的其他三个步骤，这三个步骤可由任意工作人员完成并可同时进行；
一个步骤只能由一名工作人员完成，此步骤完成后该工作人员才能进行其他步骤；
每个步骤所需时间如下表所示：
步骤 打扫卫生 整理床铺 更换客用物品 检查设备
所需时间分钟
在不考虑其他因素的前提下，若由甲单独完成一间客房的清洁工作，需要 分钟；若由甲、乙、丙合作完成四间客房的清洁工作，则最少需要 分钟．
三、解答题：本题共12小题，共96分。解答应写出文字说明，证明过程或演算步骤。
17.本小题分
计算：．
18.本小题分
解不等式组：
19.本小题分
已知，求代数式的值．
20.本小题分
如图，在中，，平分交于点，点在线段上，点在的延长线上，且，连接，，，．
求证：四边形是菱形；
若，，，求和的长．
21.本小题分
在平面直角坐标系中，函数的图象经过点和，与过点且平行于轴的直线交于点．
求该函数的表达式及点的坐标；
当时，对于的每一个值，函数的值大于函数的值且小于，直接写出的取值．
22.本小题分
为了大力支持消费者购买绿色智能家电，满足人民美好生活需要，北京市商务局发布了北京市加力支持家电以旧换新补贴实施细则，规定：活动期间，北京市居民购买电视、冰箱、洗衣机等大类家电，给予以旧换新补贴．购置一级能效家电，按照新购电器售价的给予补贴；购置二级能效家电，按照新购电器售价的给予补贴．每位消费者每类产品可补贴件，每件补贴金额不超过元．
活动期间，王先生购买了一台元的一级能效家电，可获得 元的补贴；
活动期间，王先生购买了一台二级能效的电视机和一台一级能效的冰箱，共获得以旧换新补贴元，已知电视机的售价比冰箱售价的倍还多元．求电视机和冰箱的售价各是多少元？
23.本小题分
某校九年级两个班要举行韵律操比赛．两个班各选择名选手，统计了他们的身高单位：，数据整理如下：
班
班
每班名选手身高的平均数、中位数、众数如表：
班级 平均数 中位数 众数
班
班
根据以上信息，回答下列问题：
写出表中的值；
如果某班选手的身高的方差越小，则认为该班选手的身高越整齐．据此推断：在班和班的选手中，身高比较整齐的是 班填“”或“”；
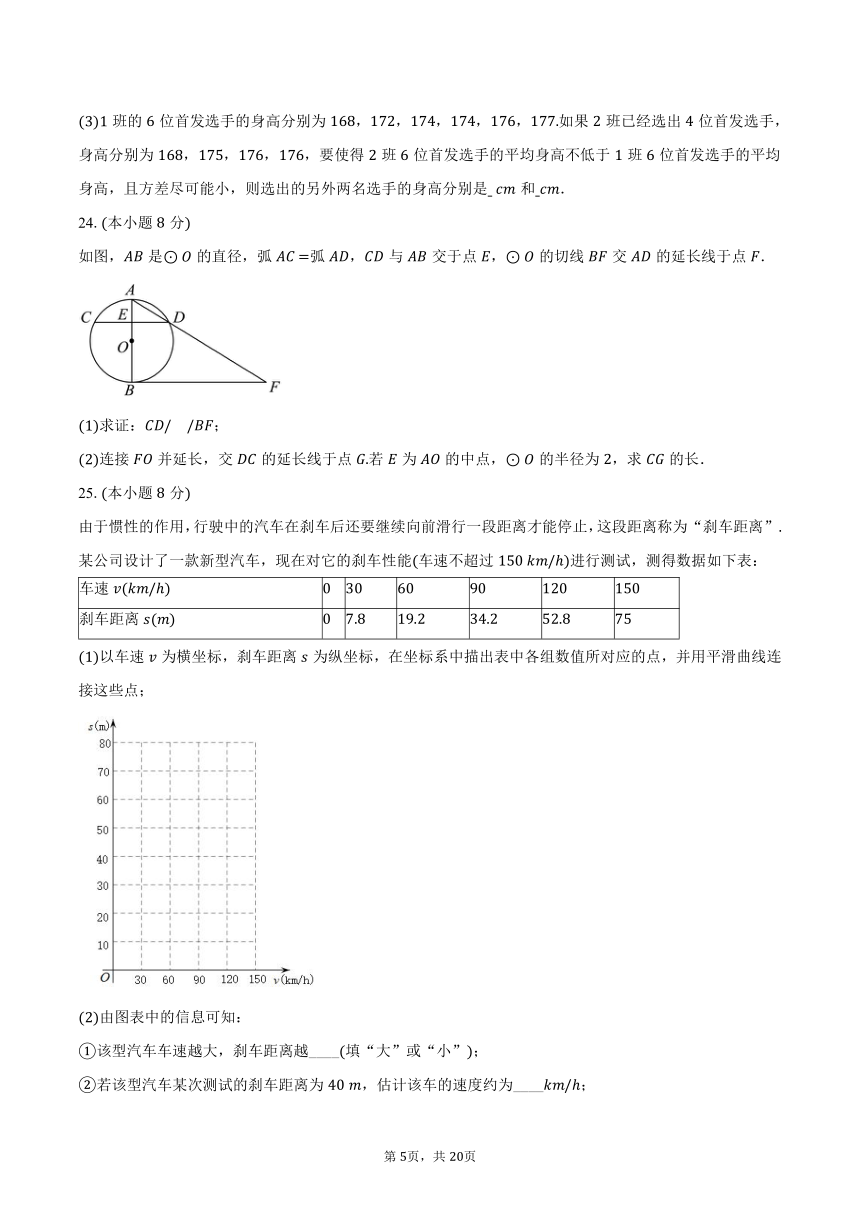
班的位首发选手的身高分别为，，，，，如果班已经选出位首发选手，身高分别为，，，，要使得班位首发选手的平均身高不低于班位首发选手的平均身高，且方差尽可能小，则选出的另外两名选手的身高分别是 和 ．
24.本小题分
如图，是的直径，弧弧，与交于点，的切线交的延长线于点．
求证：；
连接并延长，交的延长线于点若为的中点，的半径为，求的长．
25.本小题分
由于惯性的作用，行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”某公司设计了一款新型汽车，现在对它的刹车性能车速不超过进行测试，测得数据如下表：
车速
刹车距离
以车速为横坐标，刹车距离为纵坐标，在坐标系中描出表中各组数值所对应的点，并用平滑曲线连接这些点；
由图表中的信息可知：
该型汽车车速越大，刹车距离越____填“大”或“小”；
若该型汽车某次测试的刹车距离为 ，估计该车的速度约为____；
若该路段实际行车的最高限速为，要求该型汽车的安全车距要大于最高限速时刹车距离的倍，则安全车距应超过____．
26.本小题分
在平面直角坐标系中，，是抛物线上任意两点．
当时，求抛物线与轴交点的坐标；
若对于，，其中，都有，求的取值范围．
27.本小题分
已知，点，分别在射线，上，将线段绕点逆时针旋转得到线段，过点作的垂线交射线于点．
如图，当点在射线上时，点恰好是的中点，请写出与之间的关系，并证明；
如图，若与之间的关系如所求，当点在外部时，作，交射线于点；
依题意补全图形；
用等式表示线段与的数量关系，并证明．
28.本小题分
在平面直角坐标系中，的半径为，对于的弦和不在直线上的点，给出如下定义：若，且点关于弦的中点的对称点在上或其内部，则称点为弦的“关联点”．

已知点，．
在点，，中，点 是弦的关联点，其中 ；
若直线上存在的“关联点”，则的取值范围是 ；
若点是的“关联点”，且，直接写出弦的最大值和最小值．
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

17.解：
．

18.解：
解不等式得：，
解不等式得：，
不等式组的解集为．

19.解：，
，
原式
．

20.证明：，平分，
，．
，
四边形是平行四边形．
，
四边形是菱形．
解：，，，
在中，，
．
，
在中，，，
．
四边形是菱形，
．

21.解：把代入中，
得到方程组
将代入，解得，
该函数表达式为．
过点且平行于轴的直线方程为．
点在直线上，同时也在上，
把代入，得，
点的坐标为；
解：当时，需满足，
左边不等式：
整理得：，
，
，
，则，
，即，
右边不等式：，
整理得：，
，需保证，即时成立．
综合条件：且，故．

22.解：根据题意，
则可获得元的补贴；
解：设冰箱的价格为元，则电视机的价格为元．
由题意可得，冰箱可获得的补贴为或者元，电视机可获得的补贴为或元，
共获得以旧换新补贴元，
冰箱和电视机最多有一项补贴为元，
两项的补贴均不超过元：
解得：，舍去；
冰箱和电视机有一项补贴为元；
，
电视机补贴为元，
此时，，
解得：，符合题意；
，．
答：冰箱的价格为元，则电视机的价格为元．

23.班数据从小到大排列为，，，，，，，，
从中可以看出一共八个数，第四个数据为、第五个数据为，所以这组数据的中位数为：，故；
其中出现的次数最多，所以这组数的众数为，故；
故答案为：，．
根据方差的定义可以知道，方差越大，一组数据的波动越大，离散程度越大，稳定性也越小，反之亦然．
班的身高分布于，班的身高分布于，
从中可以看出，班的数据较班的数据波动较小，更加稳定，所以班的选手身高比较整齐，
故答案为：．
厘米
设班另外两名选手的身高分别为厘米，厘米，
则，
，
方差要尽可能小，
则班位首发选手的身高数据应分布于，
即：另外两名选手的身高分别是和，
故答案为：，．

24.证明：连接，，
弧弧，
，
又，
，
是的切线，
，
；
解：为中点，，
，
在中，，
，
，
，
，
，
在和中，，，
，
，
，
．

25.解：图象如图所示，
大；；
．
26.解：当时，，
令，，
解得：，，
求抛物线与轴交点的坐标为和；
，
，
，即，
总成立，
总成立，
时，
，
总成立，即，
，
，
成立即可，
；
时，
，
总成立，即，
成立即可，
，
综上所述，或．

27.证明：连接，
由题意得：点是的中点，，
，
，
，
，
，
；
解：依题意补全图形；
，
证明：在射线上取点，使得，取的中点，连接，
，
，
，
，
，
，
，，
，
，
，，
是的中点，
，，
，
，
，
，
，
，
．

28.解：点关于弦的中点的对称点在上或其内部，则称点为弦的“关联点”，
反向思考，作出关于点的对称圆，只要满足，，在上或内部，均符合题意，

，，
，
，
，
，
点到的距离为，
点在上，
同理经过计算，到的距离为均大于半径，故不符合题意，
点是弦的关联点，
连接，
，同理可求，，
，
，
，
，
故答案为：，；
同上作出关于点的对称圆，连接，

，，，，
同理可求，，，
同理可求，
，
，
，
，
的“关联点”在优弧上不包括端点，
若直线上存在的“关联点”，
则直线与优弧上不包括端点有交点，
当直线经过点时，如图：

把代入得：，
解得：，
，直线与优弧上不包括端点有交点，
当直线与相切时，如图：

记切点为，连接，记直线与轴交于点，
当时，，
解得：，
，
当，，
，
则，
，
过作轴交直线于点，
则，
由切线得性质得到：
，
点，
代入，
求得：，
，直线与优弧上不包括端点有交点，
综上所述：时，直线上存在的“关联点”，
故答案为：；
解：，
点在以为圆心为半径的圆上，
对于弦，我们固定点，调整点位置即可，
同上作出关于点对称的，
点是的“关联点”，
根据关联点的定义可知：点首先需要在关于点对称的上或者内部不包括、，
点是的“关联点”，
以为底边，作顶角为的等腰，
由圆周角定理可得：，
点又得在以为圆心，为半径的优弧上，
那么优弧必须与以为圆心为半径的圆有交点，才符合题意，
当优弧必须与以为圆心为半径的圆相切时，最小，设切点为点，如图：

由圆的对称性可知共线，，
设，则同上可得，
在中，，
，
，
解得：或舍
，
当恰好经过优弧时，此时最大，那么此时点与重合，如图：

，
，
，
综上，弦的最大值为，最小值为．

第1页，共1页

展开更多......

收起↑