资源简介

平行线性质判定专项训练提升题1
一、综合题
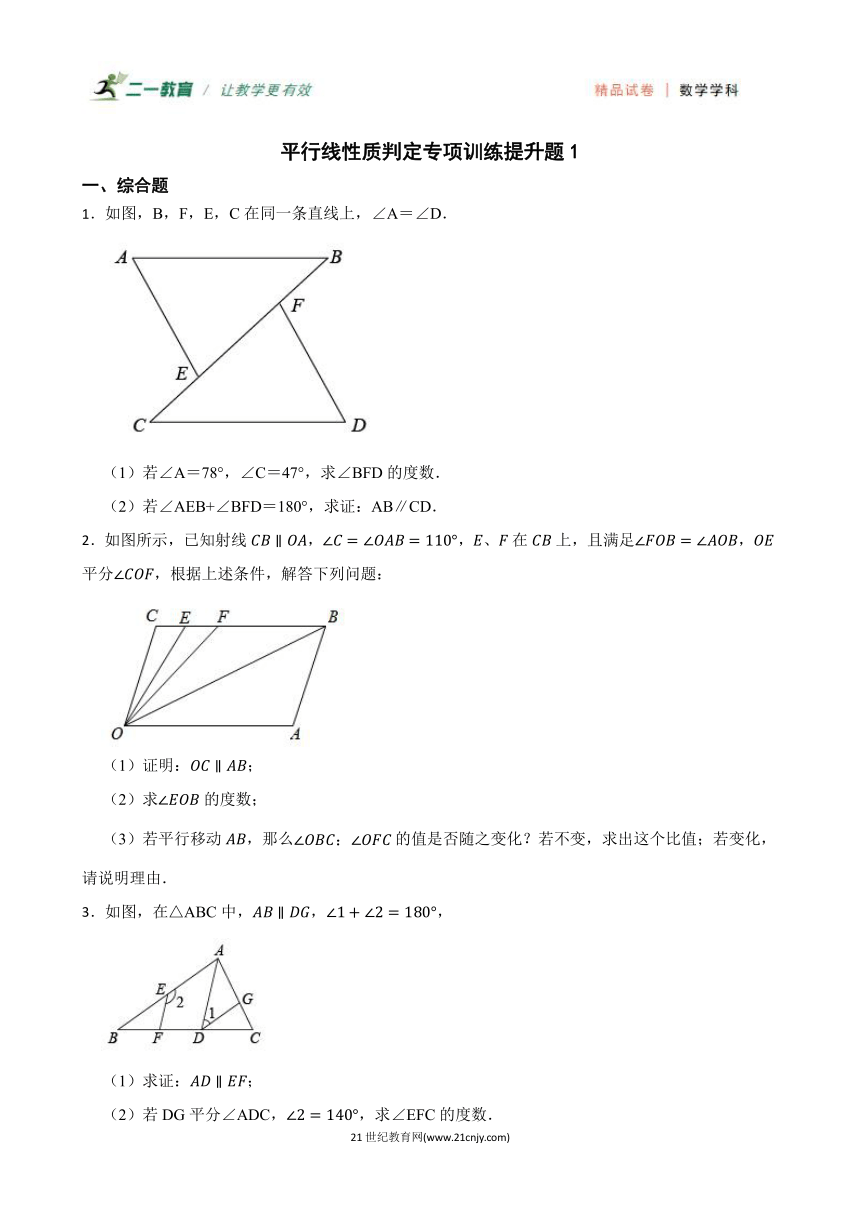
1．如图，B，F，E，C在同一条直线上，∠A＝∠D．
（1）若∠A＝78°，∠C＝47°，求∠BFD的度数．
（2）若∠AEB+∠BFD＝180°，求证：AB∥CD．
2．如图所示，已知射线，，、在上，且满足，平分，根据上述条件，解答下列问题：
（1）证明：；
（2）求的度数；
（3）若平行移动，那么的值是否随之变化？若不变，求出这个比值；若变化，请说明理由．
3．如图，在△ABC中，，，
（1）求证：；
（2）若DG平分∠ADC，，求∠EFC的度数．
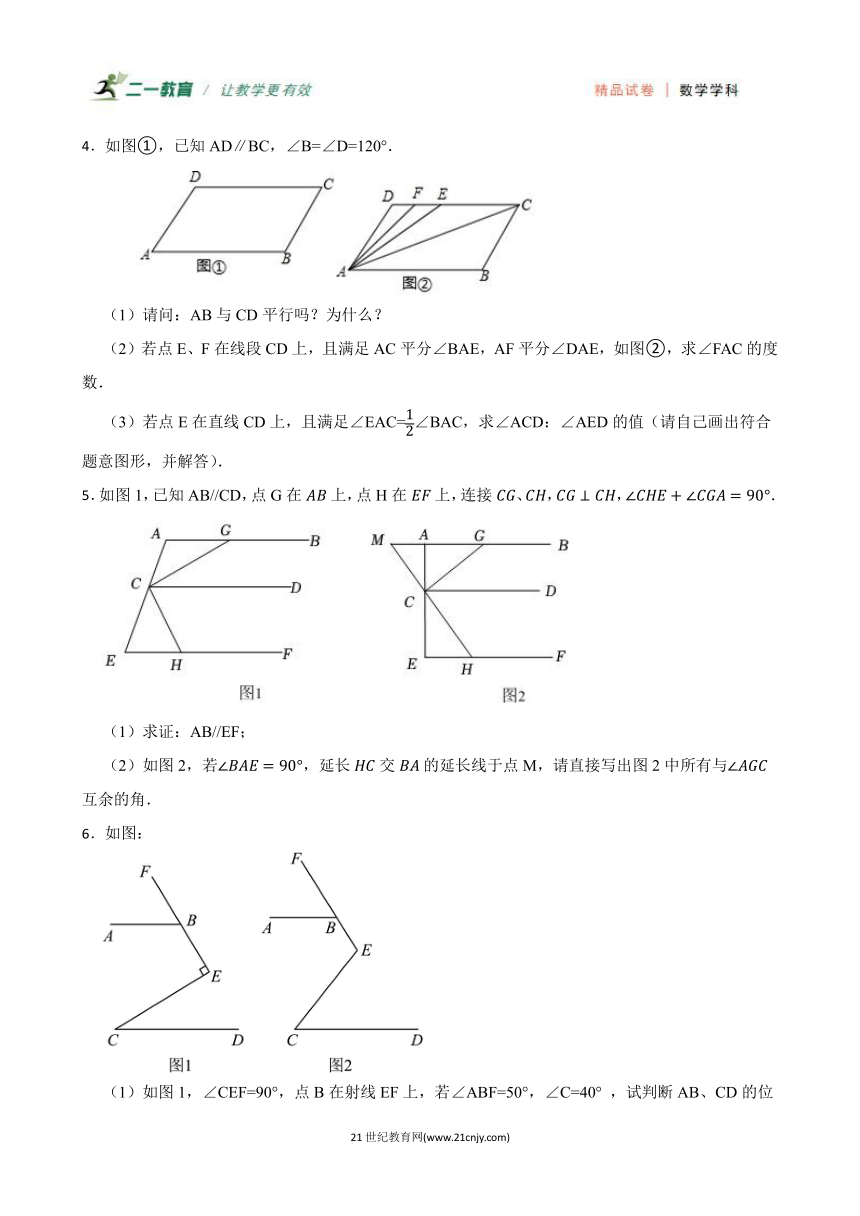
4．如图①，已知AD∥BC，∠B=∠D=120°．
（1）请问：AB与CD平行吗？为什么？
（2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．
（3）若点E在直线CD上，且满足∠EAC=∠BAC，求∠ACD：∠AED的值（请自己画出符合题意图形，并解答）．
5．如图1，已知AB//CD，点G在上，点H在上，连接、，，．
（1）求证：AB//EF；
（2）如图2，若，延长交的延长线于点M，请直接写出图2中所有与互余的角．
6．如图：
（1）如图1，∠CEF=90°，点B在射线EF上，若∠ABF=50°，∠C=40° ，试判断AB、CD的位置关系，并说明理由；
（2）如图2，∠CEF=120° ，点B在射线EF上，且．则∠ABE与∠C的数量关系为：　 　
7．如图，已知AB∥CD，EF∥MN，∠1=115°，
（1）求∠2和∠4的度数；
（2）本题隐含着一个规律，请你根据（1）的结果进行归纳：如果一个角的两边分别平行于另一个角的两边，那么这两个角　 　；
（3）利用(2)的结论解答：如果两个角的两边分别平行，其中一个角是另一个角的两倍，求这两个角的大小.
8．如图，，点O是上一点，直线经过点O，且平分，过点A作于点A，且；
（1）求的度数；
（2）连接，若，求的度数．
9．如图，，，，，点P是上的一点．
（1）求的度数；
（2）若，请判断与是否平行．
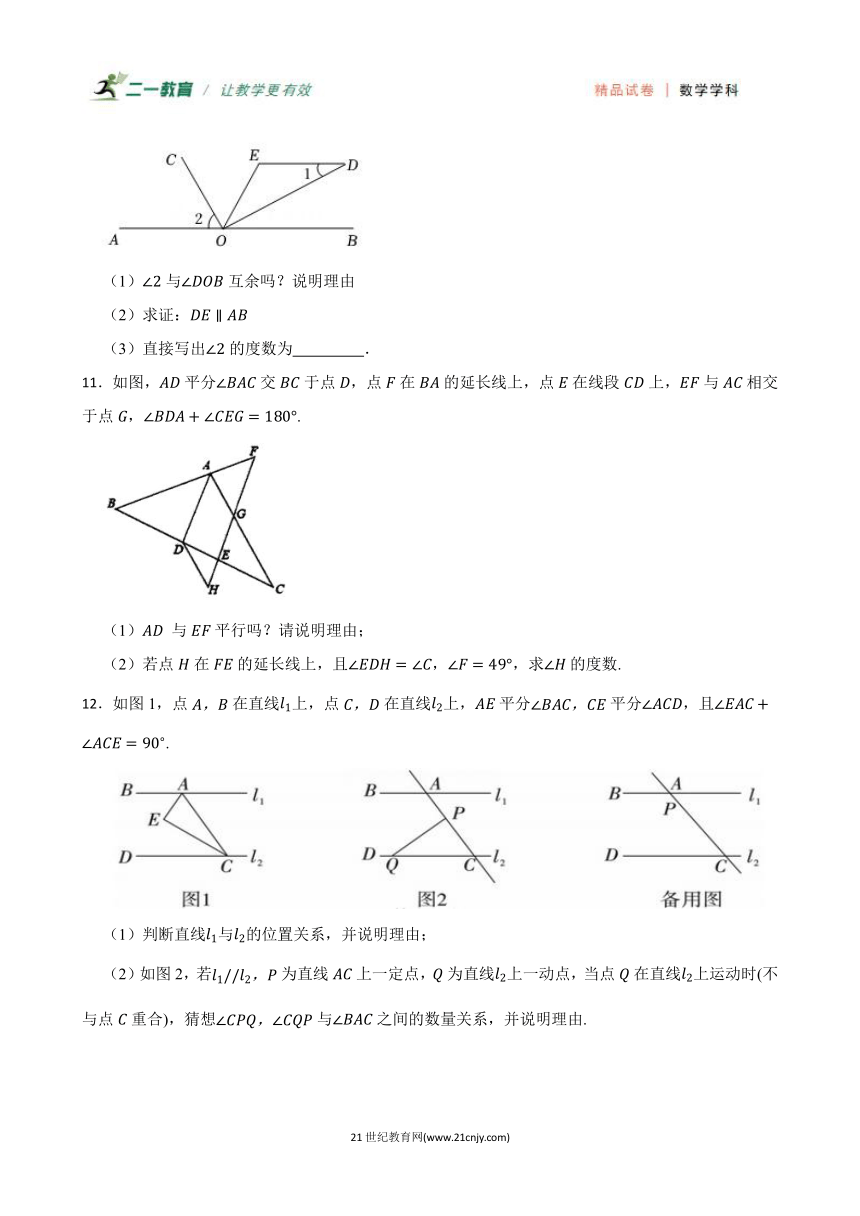
10．已知：点O为直线AB上一点，∠1与∠2互余，DO⊥OC，DO平分∠EOB，∠E=100°．
（1）与互余吗？说明理由
（2）求证：
（3）直接写出的度数为　 　．
11．如图，平分交于点，点在的延长线上，点在线段上，与相交于点，.
（1） 与平行吗？请说明理由；
（2）若点在的延长线上，且，，求的度数.
12．如图1，点在直线上，点在直线上，平分平分，且.
（1）判断直线与的位置关系，并说明理由；
（2）如图2，若为直线上一定点，为直线上一动点，当点在直线上运动时(不与点重合)，猜想与之间的数量关系，并说明理由.
13．
（1）问题情境：如图1，，，，求的度数；
（2）问题迁移：在（1）的条件下，如图2，的角平分线与的角平分线交于点F，则的度数为多少？请说明理由；
（3）问题拓展：如图3，，点P在射线上移动时（点P与点O，M，D三点不重合），记，，请直接写出与，之间的数量关系．
14．已知：如图，直线，点C是PQ，MN之间（不在直线PQ，MN上）的一个动点.
（1）若∠1与∠2都是锐角，如图1，请直接写出∠C与∠1∠2之间的数量关系.
（2）若小明把一块三角板（∠A=30°，∠C=90°）如图2放置，点D，E，F是三角板的边与平行线的交点，若∠AEN=∠A，求∠BDF的度数.
（3）将图2中的三角板进行适当转动，如图3，直角顶点C始终在两条平行线之间，点G在线段CD上，连结EG，且有∠CEG=∠CEM，给出下列两个结论：
①的值不变；
②∠GEN－∠BDF的值不变.
其中只有一个是正确的，你认为哪个是正确的？讲求出不变的值是多少.
15．如图①，，点A，C分别在射线FE和FH上，．
（1）若，则的度数为　 　；
（2）小明同学发现，无论如何变化，的值始终为定值，并给出了一种证明该发现的辅助线作法：如图②，过点A作，交CD于点M．请你根据小明同学提供的辅助线，确定该定值，并说明理由；
（3）如图③，把“”改为“”，其他条件保持不变，猜想与的数量关系，并说明理由．
16．七年级同学解决平行线问题时，遇到这样的问题，请你帮忙解决：已知AB∥CD，
（1）如图1，猜想∠AEC，∠BAE，∠DCE之间有什么数量关系不必说明理由；
（2）如图2，BE平分∠ABC，DE平分∠ADC．BE、DE所在直线交于点E，若∠FAD=40°，∠ABC=50°，求∠BED的度数；
（3）将图（2）中的线段BC沿DC所在的直线平移，使得点B在点A的右侧，∠FAD=m°，∠ABC=n°，其他条件不变，得到图3，请直接写出∠BED的度数（用含m，n的式子表示）．
17．问题：已知线段AB∥CD，在AB、CD间取一点P（点P不在直线AC上），连接PA、PC，试探索∠APC与∠A、∠C之间的关系．
（1）端点A、C同向：
如图1，点P在直线AC右侧时，∠APC﹣（∠A+∠C）＝　 　度；
如图2，点P在直线AC左侧时，∠APC+（∠A+∠C）＝　 　度；
（2）端点A、C反向：
如图3，点P在直线AC右侧时，∠APC与∠A﹣∠C有怎样的等量关系？写出结论并证明；
如图4，点P在直线AC左侧时，∠APC﹣（∠A﹣∠C）＝ ▲ 度．
18．在一次数学综合实践活动课上，同学们进行了如下探究活动：将一块等腰直角三角板的顶点G放置在直线上，旋转三角板．
（1）如图1，在边上任取一点P（不同于点G，E），过点P作，若，求的度数；
（2）如图2，过点E作，请探索并说明与之间的数量关系；
（3）将三角板绕顶点G转动，过点E作，并保持点E在直线的上方．在旋转过程中，探索与之间的数量关系，并说明理由．
19．如图，直线ABCD，直线与、分别交于点、，小安将一个含角的直角三角板按如图①放置，使点、分别在直线、上，且在点、的右侧，，．
（1）填空：　 　（填“”“”或“”）；
（2）若的平分线交直线于点，如图②．
①当ONEF，PMEF时，求的度数；
②小安将三角板保持PMEF并向左平移，在平移的过程中求的度数（用含的式子表示）．
答案解析部分
1．【答案】（1）解：∵∠A=78°，∠A=∠D，∴∠D=78°，∵∠C=47°，∴∠BFD=∠D+∠C=78°+47°=125°；
（2）证明：∵∠AEB+∠BFD=180°，∠CFD+∠BFD=180°，∴∠AEB=∠CFD，∵∠A=∠D，∴∠B=∠C，∴AB∥CD．
【解析】【分析】（1）先求出 ∠D=78°， 再计算求解即可；
（2）先求出 ∠AEB=∠CFD， 再利用平行线的判定方法证明即可。
2．【答案】（1）证明：∵，，∴，∴，∴；
（2）解：∵，∴平分，又平分，∴；
（3）解：不变．∵，∴，，∴，又∵，∴．
【解析】【分析】（1）先利用平行线的性质及角的运算和等量代换可得，从而得到；
（2）利用角平分线的定义及角的运算可得；
（3）先求出，再求出即可。
3．【答案】（1）证明：∵，∴，又∵，∴，∴．
（2）解：∵∴∵DG平分，∴∵∴．
【解析】【分析】（1）利用平行线的性质可得，再利用角的运算和等量代换可得，即可得到；
（2）先求出，利用角平分线的定义可得，再利用平行线的性质可得。
4．【答案】（1）解：平行．
如图①．
∵AD∥BC，∴∠A+∠B=180°．
又∵∠B=∠D=120°，∴∠D+∠A=180°，∴AB∥CD；
（2）解：如图②．
∵AD∥BC，∠B=∠D=120°，∴∠DAB=60°．
∵AC平分∠BAE，AF平分∠DAE，∴∠EAC=∠BAE，∠EAF=∠DAE，
∴∠FAC=∠EAC+∠EAF=（∠BAE+∠DAE）=∠DAB=30°；
（3）解：①如图3，当点E在线段CD上时，
由（1）可得AB∥CD，∴∠ACD=∠BAC，∠AED=∠BAE．
又∵∠EAC=∠BAC，∴∠ACD：∠AED=2：3；
②如图4，当点E在DC的延长线上时，
由（1）可得AB∥CD，∴∠ACD=∠BAC，∠AED=∠BAE．
又∵∠EAC=∠BAC，∴∠ACD：∠AED=2：1．
综上所述：∠ACD：∠AED=2：3或2：1．
【解析】【分析】（1）利用平行线的判定与性质求解即可；
（2）先求出 ∠DAB=60°，再求出∠EAC=∠BAE，∠EAF=∠DAE， 最后计算求解即可；
（3）分类讨论，结合图形，利用平行线的性质求解即可。
5．【答案】（1）证明：∵AB//CD，∴∠AGC=∠GCD，∵CG⊥CH，∴∠GCD+∠DCH=90°，∵∠CHE+∠CGA=90°，∴∠DCH=∠CHE，∴CD//EF．
（2）解：与∠AGC互余的角有∠ACG，∠DCH，∠M，∠CHE．
【解析】【解答】解：(2)∵∠BAE=90°，
∴∠ACG是∠AGC的余角，
∵AB∥CD，
∴∠ACD=90°，∠M=∠DCH，
∵CG⊥CH，
∴∠ACG=∠DCH，
∵AB∥EF，
∴∠M=∠CHE，
∴与∠AGC互余的角有∠ACG，∠DCH，∠M，∠CHE．
【分析】（1）由平行线的性质可得∠AGC=∠GCD，由垂直的定义可得∠GCD+∠DCH=90° ，结合 ∠CHE+∠CGA=90° ，根据余角的性质可得∠DCH=∠CHE，根据平行线的判定即证；
（2）根据余角的定义进行求解即可.
6．【答案】（1）解：理由：如图，过点E作，
∴∠ABF=∠GEF=50°，∵∠CEF=90°，，∵∠C=40°，∴∠GEC=∠C，∴EG∥CD，∴；
（2）∠ABE-∠C=60°
【解析】【解答】解：（2）过点E作EH∥AB，
则∠ABE+∠HEF=180°①，∵AB∥CD，∴EH∥CD，∴∠C=∠CEH，∵∠CEH+∠HEF=∠CEF=120°，∴∠C+∠HEF=120°②，①-②得，∠ABE-∠C=60°．故答案为：∠ABE-∠C=60°．
【分析】（1）先求出 ∠ABF=∠GEF=50°， 再求出 ∠GEC=∠C， 最后证明求解即可；
（2）利用平行线的判定与性质计算求解即可。
7．【答案】（1）解：∵AB∥CD，
∴∠2=∠1=115°，
∵EF∥MN，∴∠4+∠2=180°，
∴∠4=180°-∠2=65°；
（2）相等或互补
（3）解：由（2）可知这两个角互补，设一个角为x°，则另一个角为2x°，
根据题意可得x+2x=180，
解得x=60，
∴这两个角分别为60°和120°．
【解析】【解答】解：（2）由（1）可知如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，
故答案为相等或互补；
【分析】（1）利用平行线的性质可得∠2=∠1=115°，再结合∠4+∠2=180°，可得∠4=180°-∠2=65°；
（2）利用平行线的性质可得答案；
（3）设一个角为x°，则另一个角为2x°，根据题意列出方程x+2x=180，求出x的值即可。
8．【答案】（1）解：∵，，∴，∵，∴，∴，即的度数为；
（2）解：∵，∴，∵平分，∴，∴，∵，，∴，∴，即的度数为．
【解析】【分析】（1）利用平行线的性质可得，再利用角的运算可得；
（2）先求出，利用角平分想的定义可得，最后利用平行线的性质可得。
9．【答案】（1）解：∵∠A＝58°，∠D＝122°，∴∠A＋∠D＝180°，∴ABCD，∴∠DFE＝∠1，（两直线平行，同位角相等）∵∠1＝3∠2，∠2＝25°，∴∠DFE＝∠1＝75°；
（2）解：CEPF 理由如下：∵∠DFE＝75°，∴∠BFC＝75°（对顶角相等），∵∠BFP＝50°，∴∠PFC＝75°－50°＝25°，∵∠2＝25°，∴∠PFC＝∠2，∴CEPF．
【解析】【分析】（1）先求出 ∠A＋∠D＝180°， 再求出 ABCD， 最后根据平行线的性质求解即可；
（2）根据平行线的判定方法证明即可。
10．【答案】（1）解：互余 .理由如下：∵，∴，∴＋＝90°，即与互余
（2）证明：∵与互余，与互余∴，∴；
（3）55°
【解析】【解答】解：（3）∵，∴，∵，∴，∵DO平分，∴，∵＋＝90°，∴．故答案为：
【分析】（1）先求出 ， 再求出 ＋＝90°， 最后求解即可；
（2）利用平行线的判定方法证明求解即可；
（3）先求出，再求出，最后计算求解即可。
11．【答案】（1）解： .
理由是：∵ ，
，
∴ ，
∴ .
（2）解：∵ 平分 ，
∴ ，
∵ ，
∴ ，
∴ ，
由（1）知 ，
∴ ， ，
∴ .
【解析】【分析】（1）利用补角的性质可证得∠ADE=∠CEG，再利用同位角相等，两直线平行，可证得结论.
（2）利用角平分线的定义可证得∠BAD=∠CAD，利用内错角相等，两直线平行，可证得DH∥AC，利用平行线的性质可推出∠H=∠CGH，∠DAC=∠CGH，由此可证得结论.
12．【答案】（1）解： ∥ ，理由如下：
∵平分平分，
∴∠BAC=2∠CAE，∠ACD=2∠ACD，
∴∠BAC+∠ACD=2（∠ACD+∠CAE）=180°，
∴；
（2）解：当点P在C左侧时，∠BAC=∠CQP+∠CPQ；②当点P在C右侧时，，理由如下：
①如图，当点P在C左侧时，过P作PE∥CD，
∵l1∥l2，
∴PE∥l2，
∴∠1=∠2，∠BAC=∠EPC，
又∵∠EPC=∠1+∠CPQ，
∴∠BAC=∠CQP+∠CPQ；
②如图，当点P在C右侧时，过P作PE∥CD，
∵l1∥l2，
∴PE∥l2∥l2，
∴∠1=∠2，∠BAC=∠APE，
又∵∠EPC=∠1+∠CPQ，∠APE+∠EPC=180°，
∴∠CPQ+∠CQP+∠BAC= 180°.
【解析】【分析】(1)根据角平分线的定义可得∠BAC=2∠1，∠ACD=2∠2，结合∠1+∠2 =90°，得出∠BAC+∠ACD=180°，即可得出结论；
(2)分两种情形：①当P在C点左侧时，过点P作PE∥CD，可得PE∥l2，根据平行线性质得出∠1=∠2，∠BAC=∠EPC，再根据角的和差关系，即可得出结果；②当Q在C点右侧时，可得PE∥l2∥l2，根据平行线性质得出∠1=∠2，∠BAC=∠APE，再根据角的和差和邻补角的性质，即可求出结果.
13．【答案】（1）解：过点P作，
如图，∵，
∴，
∴，，
∵，，
∴，
，
∴．
（2）解：分别过点P和点F作，，
如图，∵，
∴，
∴，，，，
由（1）得，
∵的角平分线与的角平分线交于点F，
∴，
∴，
∴．
（3）当点P在上时，；当点P在延长线上时，；当点P在延长线上时，．
【解析】【解答】解：（3）当点P在上时，如原题图3，和（1）同理可得：；
当点P在延长线上时，如图所示，AP交CD于点E，
∵，
∴，
又∵，
；
当点P在延长线上时，如图所示，CP交AB于点F，
∵，
∴，
又∵，
∴．
综上所述，当点P在上时，；当点P在延长线上时，；当点P在延长线上时，．
【分析】（1）过点P作，利用平行线的性质可得，，再利用角的运算和等量代换可得；
（2）分别过点P和点F作，，利用平行线的性质可得，，，，再利用角平分线的定义可得，再利用角的运算和等量代换可得；
（3）分三种情况：①当点P在上时，②当点P在延长线上时，③当点P在延长线上时，再分别求解即可。
14．【答案】（1）解：∠C=∠1+∠2．
理由：如图1，过C作CD∥PQ，
∵PQ∥MN，
∴CD∥MN，
∴∠1=∠ACD，∠2=∠BCD，
∴∠ACB=∠ACD+∠BCD=∠1+∠2．
（2）解：∵∠AEN=∠A=30°，
∴∠MEC=30°，
由（1）可得，∠C=∠MEC+∠PDC=90°，
∴∠PDC=90°-∠MEC=60°，
∴∠BDF=∠PDC=60°；
（3）解：结论①的值不变是正确的，
设∠CEG=∠CEM=x，则∠GEN=180°-2x，
由（1）可得，∠C=∠CEM+∠CDP，
∴∠CDP=90°-∠CEM=90°-x，
∴∠BDF=90°-x，
∴==2（定值）， 即的值不变，值为2．
【解析】【分析】（1）过C作CD∥PQ，利用平行线的性质可得∠1=∠ACD，∠2=∠BCD，再利用角的运算和等量代换可得∠ACB=∠ACD+∠BCD=∠1+∠2；
（2）先求出∠MEC=30°，再求出∠PDC=90°-∠MEC=60°，即可得到∠BDF=∠PDC=60°；
（3）设∠CEG=∠CEM=x，则∠GEN=180°-2x， 求出∠BDF=90°-x，再代入计算可得==2。
15．【答案】（1）60°
（2）解：该定值为90°．理由如下：∵，，∴，．∵，∴．∴．∴．∴无论如何变化，的值始终为定值，且该定值为90°．
（3）解：．理由如下：过点A作，交CD于点N，如图所示，
∵，，∴，．∵，∴．∴．∴．
【解析】【解答】（1）解：过点F作FG∥AB，如图所示，
∵FG∥AB，∠FAB＝150°，∴∠AFG＋∠FAB＝180°，∴∠AFG＝180° ∠FAB＝180° 150°＝30°，∵∠EFH＝90°，∴∠CFG＝∠EFH ∠AFG＝90° 30°＝60°，∵AB∥CD，∴FG∥CD，∴∠HCD＝∠CFG＝60°．故答案为：60°；
【分析】（1）过点F作FG∥AB，根据平行线的性质可得∠AFG＝180° ∠FAB＝30°，从而求出∠CFG＝∠EFH ∠AFG＝60°，由AB∥CD，FG∥AB，可得FG∥CD，根据平行线的性质可得∠HCD＝∠CFG＝60°；
（2）由，，根据平行线的性质可得， ，由AB∥CD可得，从而推出∠FAB-∠HCD=∠FAB-∠BAM=∠FAM=90°，据此即可得解；
（3）．理由：过点A作交CD于点N，利用平行线的性质可得∠FAN=180°-∠EFH=60°，∠HCD=∠ANC，由AB∥CD可得∠BAN=∠ANC，从而得出∠BAN=∠HCD，根据即可得解．
16．【答案】（1）解：∠AEC=∠BAE+∠DCE，理由如下：如图1，作EF∥AB，则有EF∥CD，
∴∠1=∠BAE，∠2=∠DCE，∴∠AEC=∠1+∠2=∠BAE+∠DCE；
（2）解：如图2，过点E作EH∥AB，
∵AB∥CD，∠FAD=40°，∴∠ADC=∠FAD=40°，∵DE平分∠ADC，∴∠EDC=∠ADC=20°，∵BE平分∠ABC，∠ABC=50°，∴∠ABE=∠ABC=25°，∵AB∥CD，∴AB∥CD∥EH，∴∠BEH=∠ABE=25°，∠DEH=∠EDC=20°，∴∠BED=∠BEH+∠DEH=45°；
（3）解：∠BED=180°-n°+m°
【解析】【解答】解：(3)过点E作EG∥AB，如图：
∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=∠FAD=m°，∴∠ABE=∠ABC=n°，∠CDE=∠ADC=m°，∵AB∥CD，∴AB∥CD∥EG，∴∠BEG=180°-∠ABE=180°-n°，∠CDE=∠DEG=m°，∴∠BED=∠BEG+∠DEG=180°-n°+m°．
【分析】（1）根据平行线的性质即可得出结论；
（2）过点E作EH∥AB，根据平行线的性质和角平分线的定义，即可得出结论；
（3）过点E作EG∥AB，根据平行线的性质和角平分线的定义，即可得出结论。
17．【答案】（1）0；360
（2）解：，证明：过点P作，
，，，，，，；
【解析】【解答】解：（1）如图：过点P作，
，，，，，，度，
故答案为：0；
如图：过点P作，
，，，，，，度，
故答案为：360；
（2）如图：过点P作，
，，，，，，，
故答案为：180．
【分析】（1）利用平行线的性质和角的运算求解即可；
（2）利用平行线的性质和判定方法求解即可。
18．【答案】（1）解：∵，
∴，
∵，，
∴；
（2）解：，
理由：如图，过点F作，
∵，
∴，
∴，，
∴，
∵，
∴；
（3）解：①如图1中，当点F在直线的上方时，过点F作，
∵，
∴，
∴，，
∵，
∴；
②当点F在直线与直线之间时，过点F作，如下图：
由（2）可知：；
③当点F在直线的下方时，过点F作，
∵，
∴，
∴，，
∵，
∴．
综上所述，①当点F在直线的上方时，；
②当点F在直线与直线之间时，；
③当点F在直线的下方时，．
【解析】【分析】（1）先利用平行线的性质可得，再结合，求出∠2的度数即可；
（2）过点F作FP//AB，利用平行线的性质可得，，再利用角的运算可得；
（3）分三种情况：①当点F在直线的上方时，过点F作，②当点F在直线与直线之间时，过点F作，③当点F在直线的下方时，过点F作，再分别求解即可。
19．【答案】（1）=
（2）解：①，，，，，，平分，，，，；②点在的右侧时，如图②，
，，，，，，平分，，，；点在的左侧时，如图，
，，，，，，，平分，，，综上所述，的度数为或．
【解析】【解答】（1）解：过点作，
，，，，，故答案为：.
【分析】（1）利用平行线的性质可得，再利用角的运算和等量代换可得，从而得解；
（2）①利用平行线的性质可得，再利用角平分线的定义和平行线的性质可得；
②分两种情况： 第一种情况，当在的右侧时， 第二种情况，当点在的左侧时，分别画出图象再求解即可。
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑