资源简介

角度大题计算题专项训练2
一、解答题
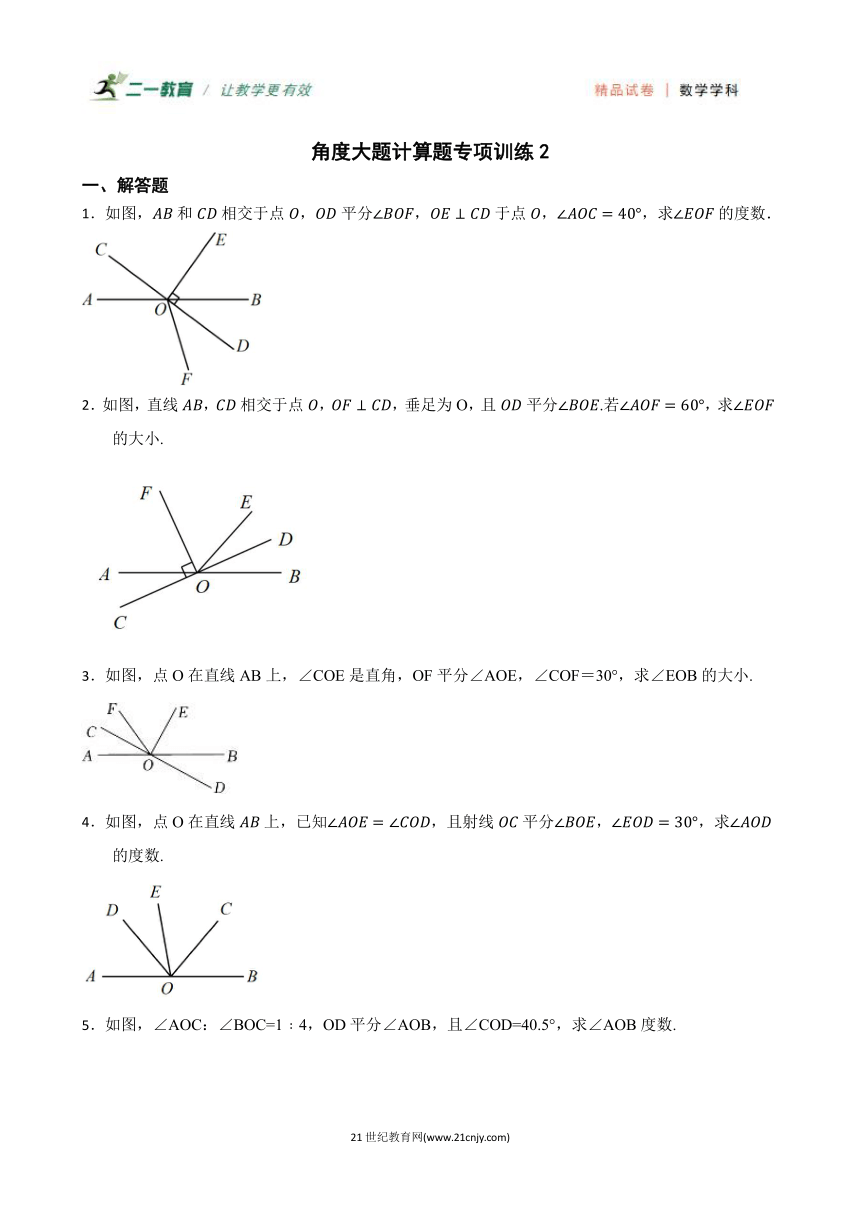
1．如图，和相交于点，平分，于点，，求的度数．
2．如图，直线，相交于点，，垂足为O，且平分.若，求的大小.
3．如图，点O在直线AB上，∠COE是直角，OF平分∠AOE，∠COF＝30°，求∠EOB的大小.
4．如图，点O在直线上，已知，且射线平分，，求的度数.
5．如图，∠AOC：∠BOC=1﹕4，OD平分∠AOB，且∠COD=40.5°，求∠AOB度数.
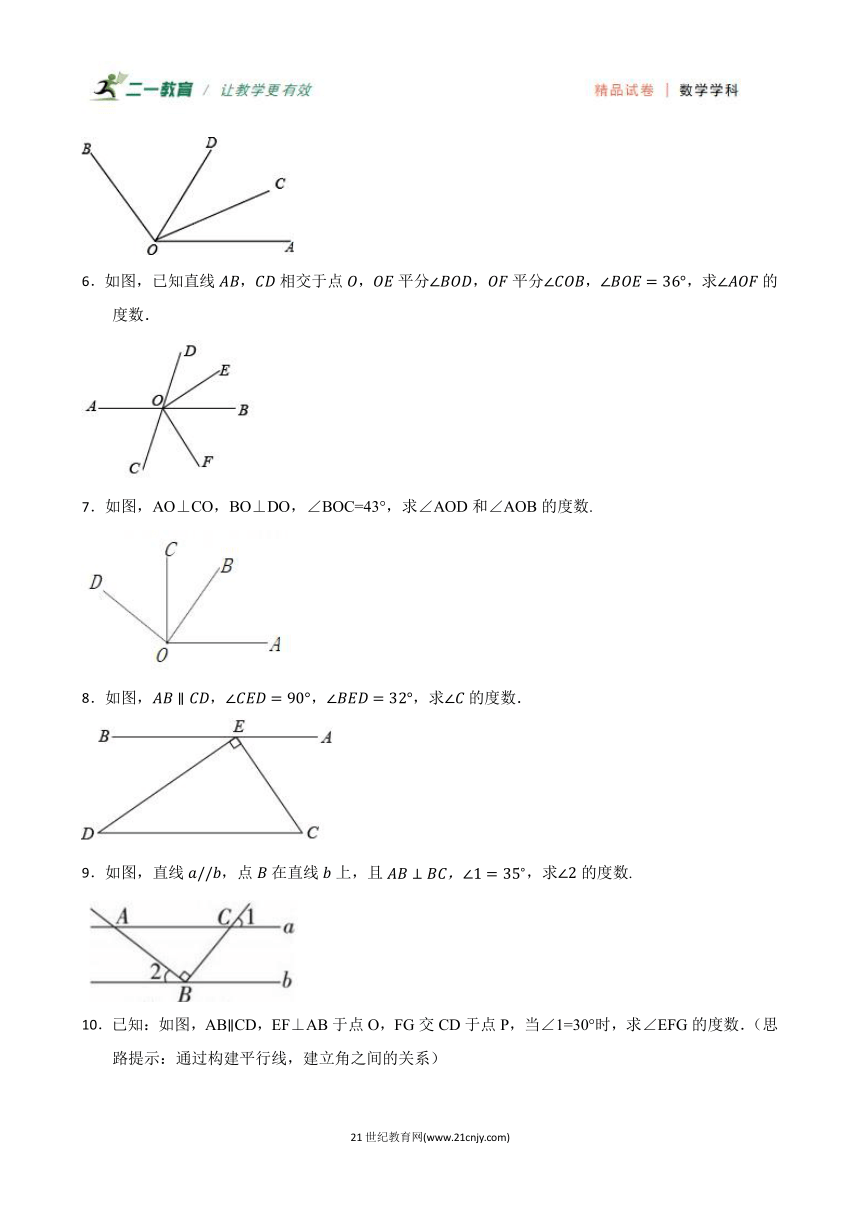
6．如图，已知直线，相交于点，平分，平分，，求的度数．
7．如图，AO⊥CO，BO⊥DO，∠BOC=43°，求∠AOD和∠AOB的度数.
8．如图，，，，求的度数．
9．如图，直线，点在直线上，且，求的度数.
10．已知：如图，ABCD，EF⊥AB于点O，FG交CD于点P，当∠1=30°时，求∠EFG的度数．（思路提示：通过构建平行线，建立角之间的关系）
11．如图，直线AB和CD相交于点O，OA平分∠COE，∠COE：∠EOD＝4：5，求∠BOD的度数．
12．如图，AB，CD交于点O，OA⊥OE，OF平分∠BOC，∠COF＝68°．求∠DOE的度数．
13．如图，在△ABC中，AB＝AC，AD为BC边上的中线，∠CAD＝40°，EF为过点A的一条直线，且EF∥BC，求∠BAE的度数．
14．如图，已知DE∥BC，CD是∠ACB的平分线，∠ABC=68°，∠ACB=42°，求∠EDC、∠BDC的度数．
15．如图，AB∥CD，点E为CD上一点，连接BE，过点E作EG平分∠BED，作EF⊥EG，若∠B＝64°，求∠CEF的度数．
16．如图，直线与相交于点，平分，若，求的度数．
17．如图，直线AB和CD相交于点O，若，OA平分，求的度数．
答案解析部分
1．【答案】解：∵，
∴，
∵和相交于点，
∴，
∵平分，
∴，
∴．
【解析】【分析】由垂直的定义可得，利用对顶角相等可得，根据角平分线的定义可得，利用角的和差关系即可求解.
2．【答案】解：∵，
∴，
∵，
∴，
∵平分，
∴，
∴.
【解析】【分析】由垂直的定义得∠COF=∠DOF=90°，由角的和差及对顶角相等得∠AOC=∠BOD=30°，由角平分线的定义得∠DOE=∠BOD=30°，进而根据角的和差，由∠EOF=∠FOD-∠EOD即可算出答案.
3．【答案】解：∵∠COE是直角，
∴∠COE＝90°，
又∵∠COE＝∠COF+∠FOE，∠COF＝30°，
∴∠FOE＝90°﹣30°＝60°，
又∵OF平分∠AOE，
∴∠AOE＝2∠FOE＝120°，
又∵∠AOE+∠BOE＝180°，
∴∠BOE＝180°﹣120°＝60°.
【解析】【分析】由题意可得∠COE＝90°，则∠FOE=∠COE-∠COF=60°，由角平分线的概念可得∠AOE＝2∠FOE＝120°，然后根据邻补角的性质进行计算.
4．【答案】解：∵，
∴，即，
∵射线平分，
∴，则，
∵，
∴，
∴.
【解析】【分析】由已知条件可知∠AOE=∠COD，结合角的和差关系可得∠AOD=∠COE，根据角平分线的概念可得∠BOC=∠COE=∠AOD，结合平角的概念可得3∠AOD+30°=180°，据此计算.
5．【答案】解：∵∠AOC：∠BOC=1：4，OD平分∠AOB，且∠COD=40.5°
∴∠AOC=∠AOB，∠AOD=∠AOB
∴∠COD=∠AOD ∠AOC=∠AOB ∠AOB=∠AOB
∴∠AOB=40.5°
解得∠AOB=135°即∠AOB的度数是135°.
【解析】【分析】 由已知条件可得∠AOC=∠AOB，根据角平分线的概念可得∠AOD=∠AOB，则∠COD=∠AOD ∠AOC=∠AOB ∠AOB=∠AOB，然后结合∠COD的度数就可求出∠AOB的度数.
6．【答案】解：∵，平分，平分，
∴，
∴，
∵，
∴，
∵，
∴．
【解析】【分析】利用角平分线的定义、角的运算和等量代换求解即可。
7．【答案】解：∵AO⊥CO，BO⊥DO，
∴∠BOD=∠AOC=90°，
∴∠AOB=∠AOC-∠BOC=90°-43°=47°，
∴∠AOD=∠BOD+∠AOB=90°+47°=137°.
∴∠AOD的度数为137°，∠AOB的度数为47°
【解析】【分析】利用垂直的定义可证得∠BOD=∠AOC=90°，可求出∠AOB的度数，再根据∠AOD=∠BOD+∠AOB，代入计算求出∠AOD的度数.
8．【答案】解：，，
．
∵AB∥CD
∴．
【解析】【分析】根据平角的定义列式求出∠AEC的度数，再根据二直线平行，内错角相等，求∠C的度数即可.
9．【答案】解：如图，
∵ ，
∴∠3=∠1=35°，
∴∠2=180°-∠ABC-∠3
=180°-90°-35°
=55°.
【解析】【分析】根据平行线的性质得出∠3的度数，再根据平角的定义列式求∠2的度数即可.
10．【答案】解：过点F作MN∥CD
∵MN∥CD，∠1=30°
∴∠2=∠1=30°（两直线平行，同位角相等）
∵MN∥CD，AB∥CD
∴AB∥MN（平行于同一直线的两条直线平行）
∴∠3=∠4（两直线平行，同位角相等）
∵EF⊥AB，
∴∠4=90°
∴∠3=∠4=90°
∴
【解析】【分析】过点F作MN∥CD，利用平行线的性质可得∠2=∠1=30°，∠3=∠4，再利用角的运算可得。
11．【答案】解：∵ ∠COE：∠EOD＝4：5 ， ∠COE+∠EOD＝180°，
∴，
又∵ OA平分∠COE ，
∴∠AOE=∠AOC=40°，
∴ ∠BOD =∠AOC=40°
【解析】【分析】求∠BOD的度数，只需求出它的对顶角∠AOC的度数即可（对顶角相等），由图可得，∠COE+∠EOD=180°（邻补角互补），再结合已知条件∠COE：∠EOD＝4：5 ，可求出∠COE=80°，又根据OA平分∠COE（从一个角的顶点出发，把这个角平分成两个相等的角的射线，叫做这个角的平分线） ，可知 ∠AOC=40°，最后得出∠BOD =40°.
12．【答案】解：∵ OF平分∠BOC， ∠COF＝68°，
∴∠BOC=2∠COF=136°，
∴∠BOD=180°-∠BOC=180°-136°=44°，
∴∠AOC=∠BOD=44°，
∵OA⊥OE， 即∠AOE=90°，
∴∠DOE=180°-∠AOC-∠AOE=180°-44°-90°=46°.
【解析】【分析】根据角平分线定义求出∠BOC，再根据邻补角定义求出∠BOD，根据对顶角相等求出∠AOC，最后根据平角的定义求∠COE，即可解答.
13．【答案】解：∵AB=AC， AD为BC边上的中线，
∴∠B=∠C，∠BAD=∠CAD=40°（三线合一），
∴∠BAC=∠BAD+∠CAD=80°，
∴，
∵EF∥BC，
∴∠BAE=∠B=50°.
【解析】【分析】根据等腰三角形的性质求出∠B=∠C，∠BAD=∠CAD，则可求出∠BAC的度数，然后根据等腰三角形的性质和三角形内角和定理求出∠B的度数，再根据平行线的性质求∠BAE度数即可.
14．【答案】解：∵ CD是∠ACB的平分线（已知），
∴（角平分线的定义），
∵DE∥BC（已知），
∴（两直线平行，内错角相等），
∵，
∴．
【解析】【分析】根据角平分线的概念得∠BCD=∠ACB=21°，根据平行线的性质得∠EDC=∠BCD=21°，然后根据内角和定理进行计算.
15．【答案】解：∵AB∥CD，
∴∠B=∠DEB=64°，
∵ EG平分∠BED ，
∴，
∵ EF⊥EG ，
∴∠GEF=90°，
∴ ∠CEF =180°-∠DEG-∠GEF=180°-32°-90°=58°，
∴∠CEF=58°
【解析】【分析】根据平行线的性质（两直线平行，内错角相等）可得∠B=∠DEB=64°，再利用角平分线的定义（从一个角的顶点引出一条射线，把这个角分成完全相同的角，这条射线叫做这个角的角平分线）可得∠DEG=32°，然后根据垂直定义可得∠GEF=90°，最后利用平角进行计算即可求出∠CEF的度数.
16．【答案】解： 平分，
，
【解析】【分析】根据角平分线的概念得∠BOD=∠BOE=∠DOE，根据已知条件得∠DOE∶∠COE=2∶3，据此可求出∠DOE、∠BOD的度数，然后根据邻补角的性质进行计算.
17．【答案】解：∵∠BOD=40°，
∴∠AOC=∠BOD=40°.
∵OA平分∠EOC，
∴∠AOE=∠AOC=40°，
∴.
【解析】【分析】 根据对顶角的性质可得∠AOC=∠BOD=40°，根据角平分线的概念可得∠AOE=∠AOC=40°，然后根据平角的概念进行计算.
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑