资源简介

(共47张PPT)
第八章、第九章
复习总结
-、平方根：
①定义：
②性质：
一般地，如果一个数x的平方等于a,即 ,那么这个数x叫作a的平方根.
正数有两个平方根，它们互为相反数；
0的平方根是0；
负数没有平方根；
③开平方：
求一个数的平方根的运算叫作开平方.
④平方根等于它本身的数有哪些？
答：0
二、算术平方根
定义：
正数a有两个平方根，其中正的平方根 叫作a的算术平方根.
①算术平方根等于它本身的数有哪些？
答：0，1
三:初中涉及的三种非负数：
①|a| ② ③
三、立方根：
①定义：
②性质：
一般地，如果一个数x的立方等于a,即 ,那么这个数x叫作a的立方根.
正数的立方根是正数；
0的立方根是0；
负数的立方根是负数；
③开立方：
求一个数的立方根的运算叫作开立方.
④立方根等于它本身的数有哪些？
答：0和-1或1.
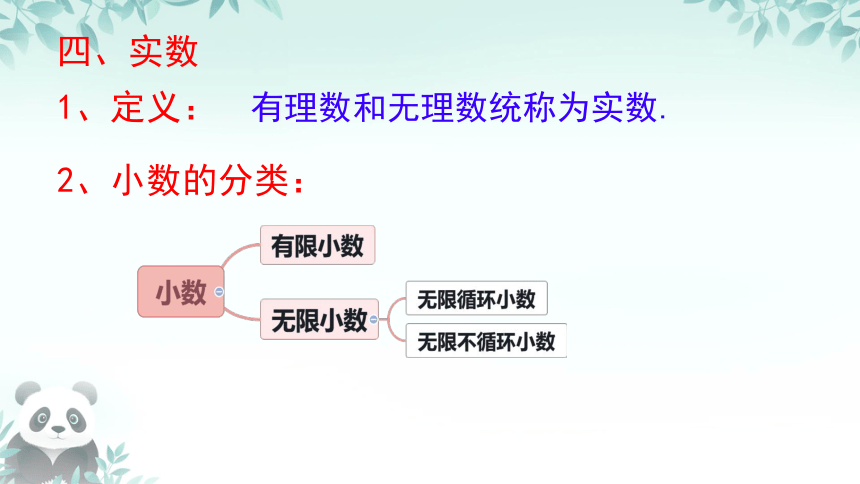
四、实数
1、定义：
有理数和无理数统称为实数.
2、小数的分类：
3、有理数的定义：
4、无理数的定义：
有限小数和无限循环小数称为有理数.
无限不循环小数称为有理数.
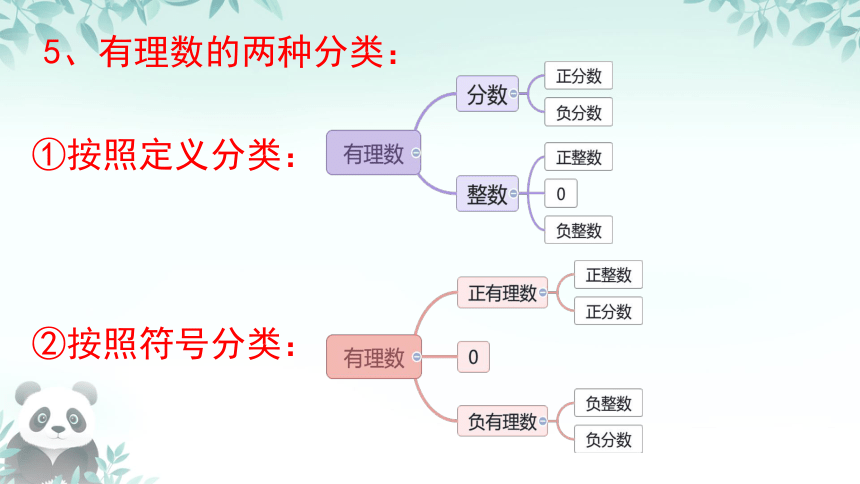
5、有理数的两种分类：
①按照定义分类：
②按照符号分类：
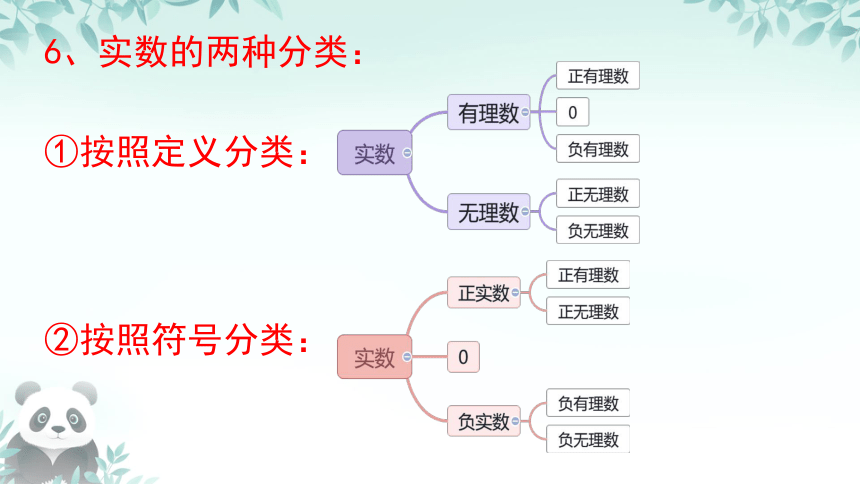
6、实数的两种分类：
①按照定义分类：
②按照符号分类：
7、实数与数轴的关系：
每一个实数都可以用数轴上的一个点来表示.
数轴上每一个点都表示一个实数.
8、实数的运算顺序：
先算乘方、开方，再算乘除，最后再算加减，有括号的先算括号内的，同级运算从左往右的顺序计算.
五、平面直角坐标系
1、概念：
在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系.
2、平面直角坐标系的三要素：
①两个数轴
②两个数轴互相垂直
③原点重合
3、坐标平面
象限以及各个象限的符号特征：
第一象限（+，+）
第二象限（-，+）
第三象限（-，-）
第四象限（+，-）
原点的表示：
通常用字母O表示，坐标为（0，0）；
4、坐标轴x、y轴
x轴上的点（x,0)
y轴上的点（0，y)
坐标轴上的点不属于任何象限
5、特殊直线
平行于x轴的直线上的点：
平行于y轴的直线上的点：
纵坐标相同；
横坐标相同；
一、三象限内两坐标轴上的角平分线上的点的特点:
二、四象限内两坐标轴上的角平分线上的点的特点:
横坐标=纵坐标
横坐标和纵坐标互为相反数
6、平面直角坐标系建立的一般步骤:
①选原点
②作两轴
③定坐标系
7、图形的平移
平移后图形的大小、位置的变化：
平移前后图形的形状、大小完全相同，位置改变
8、点的平移
点（x,y)右移a(a>0)个单位长度：
点（x,y)左移a(a>0)个单位长度：
点（x,y)上移a(a>0)个单位长度：
点（x,y)下移a(a>0)个单位长度：
(x+a,y)
(x-a,y)
(x,y+a)
(x,y-a)
1、求下列各数的平方根：（3分）
（1）64 （2）0.0081 （3）
答案：（1）±8 （2）±0.09 （3）±5
2、判断题（4分）
（1）4是16的平方根
（2）16的平方根是±4
（3）-5是25的平方根
（4）25的平方根是5
（ √ ）
（ √ ）
（ √ ）
（ × ）
3、计算题（4分）
（1）若x+3是16的平方根，则x的值为？
答案：1或-7
导学：根据平方根的性质，正数的平方根有两个，它们互为相反数；给学生三分钟时间，独立完成，老师讲解，根据掌握情况，再选择是否讨论.
（2） -16=0; (3)
答案：（2）x=±4 (3)x=-3或x=-9
每道题2分
导学：目前学的解方程一定要移项、系数化为1，注意根的个数.给学生三分钟时间，独立完成.
（4）（4分）若x是9的算术平方根，则x=
若x的算术平方根是9，则x=
答案：3； 81；
导学：算术平方根只有一个，并且是非负数，一定要仔细审题，看题目所问是平方根还是算术平方根.给学生三分钟时间，独立完成.
（5）25的平方根是多少？
（6）25的算术平方根是多少？
（7） 是多少？
（8） 的算术平方根是多少？
（9） 的平方根是多少？
一共5分
答案：
（5）±5；
（6）5；
（7）5；
（8）
（9）
导学：一定要仔细审题，看题目所问是平方根还是算术平方根以及开几次根号.
4、（2分） -3的相反数是多少？绝对值是多少？
答案：3- ；3-
导学：实数的相反数和绝对值与有理数的一样，绝对值具有非负性，一定要判断绝对值里面的数是正数还是负数.
5、（2分）在数轴上，点A、点B所对应的数分别是 和 ，那么A,B两点之间的距离为多少？
答案：
导学：数轴上求两个数a、b的距离问题，只需要|a-b|或者|b-a|,去绝对值一定要看绝对值里面的数的正负.
6、计算（2分）
答案：x=-2
导学：注意立方根的性质，任何实数只有一个立方根，同理，一元三次方程也只有一个解，和平方根进行区别，给学生两分钟时间，独立完成.
二、求下列个数的整数部分和小数部分（4分）
（1）
（2）
答案：（1）整数部分是3，小数部分是
（2）整数部分是3，小数部分是
导学：无理数求整数部分和小数部分，一定要弄清楚无理数在哪两个整数范围，再判断整数部分和小数部分
2、若 的整数部分为a，小数部分为b，
求
解：∵
∴
∴a=3,b=
∴ =6
导学：无理数求整数部分和小数部分，一定要弄清楚无理数在哪两个整数范围，再判断整数部分和小数部分
小组讨论五分钟，找同学们来讲
三、计算（5分）
（1） （2）
答案：全部都是 .
解：原式=-1+2- -2
=-1-
（5分）
4、（5分）如图，已知点A,B,C在数轴上表示的数分别为a,b,c,请化简：
a
b
0
c
导学：对于算术平方根去根号问题，可以直接化成绝对值问题，
即 ；
由于立方根没有非负性，则可以直接去根号，即 =a
学生独立完成，再讨论五分钟
a
b
0
c
解：有数轴可知a原式=|a|-|a+b|-(a-c)+|b-c|
=-a-(-a-b)-a+c+(-b+c)
=-a+a+b-a+c-b+c
=-a+2c
5、判断下列各点的象限（4分）
（1）（2，3）
（2）（-100，12）
（3）（-3，-50）
（4）（9，-8）
导学：利用四个象限符号特征进行判断，注意第二象限和第四象限，不要弄混.
6.（4分） 点B（a-1，a2-9）在x轴负半轴上，则B点的坐标是__________.
解：由题意可知，
a=±3
又∵在x轴负半轴上
∴a=-3 ∴B（-4，0）
导学：x轴上的坐标特点，纵坐标为0；学生可以根据题目所给条件进行解答.
7、（2分）（1）点P（2，m）到x轴的距离为3，则点P的坐标为
每道题三分
答案：（1）（2，3）或（2，-3）
导学：到x轴的距离是纵坐标的绝对值，到y轴的距离是横坐标的绝对值.
8、（4分）点C到x轴的距离为1，到y轴的距离为3，则C点的坐标是______.
答案：（3,1）（-3,1）
（-3,-1）（3,-1）
导学：到x轴的距离是纵坐标的绝对值，到y轴的距离是横坐标的绝对值.
9、（6分）在平面直角坐标系中，有一点P（-4，2），若将P：
(1)向左平移2个单位长度，所得点的坐标为______；
(2) 向下平移4个单位长度，所得点的坐标为______；
(3)先向右平移5个单位长度，再向上平移3个单位长度，所得坐标为_______。
答案：（-6，2）；（-4，-2）；（1，5）
导学：平面直角坐标系中，平移有以下特点：①对于横坐标：右加左减；②对于纵坐标：上加下减；
10、（2分）在平面直角坐标系，将点A（-1，2）平移到点B(3,7),请问点A如何平移的？
答案：向右平移4个单位长度，再向上平移5个单位长度。
导学：平面直角坐标系中，平移有以下特点：①对于横坐标：右加左减；②对于纵坐标：上加下减；
11、（2分）已知点M（3a-9,1-a),将点M向左平移3个单位长度落在y轴上，则a为多少？
解：由题意可知，
3a-9-3=0
a=4
导学：根据点在平面直角坐标系平移的特点，右加左减，上加下减；再根据y轴上坐标的特点：横坐标为0进行解题.
12、（4分）如果点P（m+3,m-1）在平面直角坐标系的坐标轴上，则点P的坐标为
每道题三分
答案：（2）（0，-4）或（4，0）
导学：坐标轴上的点的坐标特征：①x轴上的点纵坐标为0；②y轴上的点的横坐标为0.由于本题目并没有说明点在哪个轴上，所以要考虑全面.
13.（2分）已知点A（m，-2），点B（3，m-1），且直线AB∥x轴，则m的值为 。
m=-1
导学：①与x轴平行的直线上所有点的纵坐标相等；②与y轴平行的直线上所有点的横坐标相等.
14、（5分）已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
（1）点Q的坐标为（1，5），直线PQ//y轴；
（2）点P到x轴、y轴的距离相等.
答案：（1）P(1,14)
(2)P(-12,-12)或（-4，4）
导学：①与y轴平行的直线上所有点的横坐标相等；②到两轴距离问题一般情况下有好几种可能，计算时要考虑全面.
15、（5分）已知点A（2，3），
B（-4，2），O（0,0）。
求△AOB的面积。
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
O
A
B
C
D
E
1
2
3
导学：对于平面直角坐标系中求图形面积问题，一般有两种方法：①分割法；②补全法
下 课
Thanks!
https://www.21cnjy.com/recruitment/home/fine

展开更多......

收起↑