资源简介

(共17张PPT)
第2课时 长方体、正方体体积公式的推导
3 长方体和正方体
人教版五年级数学下册
学习目标
1.理解、掌握长方体体积的计算方法的推导过程，体会体积单位的实际意义。
2.猜想、验证、推导长方体体积计算公式，培养学生分析、归纳、推理以及抽象概括的能力。
3.进一步发展动手操作能力与空间想象能力。
4. 感悟数学知识内在联系的逻辑之美。
课前导入
1.什么叫体积？
3.你能比画出1cm3、1dm3、1m3的大小吗？
2.常用的体积单位有哪些？
昨天，我到超市买了一箱饮料和一块香皂，怎样才能知道它们的体积大小呢
香皂
你有什么好办法测量出它们的体积呢？
新知探究
（教科书第29页）
怎样计算长方体的体积呢？
求长方体的体积就是看长方体有多少个体积单位。
把长方体分成若干单位体积的小正方体，就可以……
动手小实验
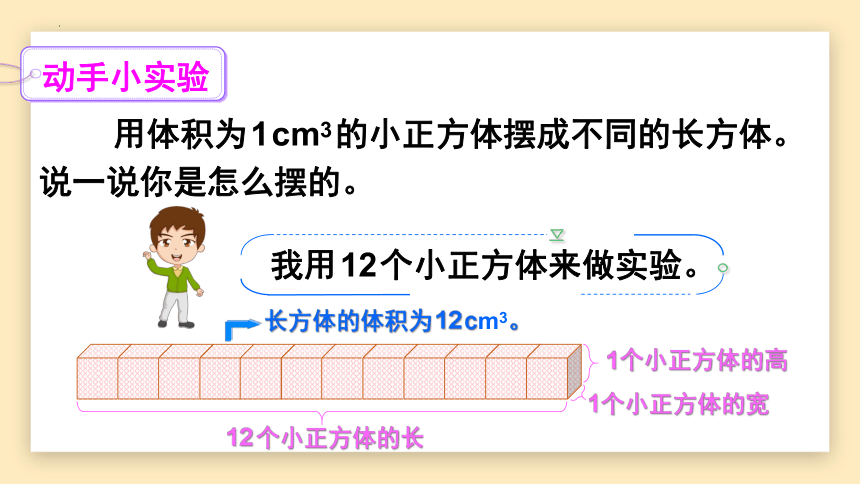
用体积为1cm3的小正方体摆成不同的长方体。说一说你是怎么摆的。
我用12个小正方体来做实验。
12个小正方体的长
1个小正方体的宽
1个小正方体的高
长方体的体积为12cm3。
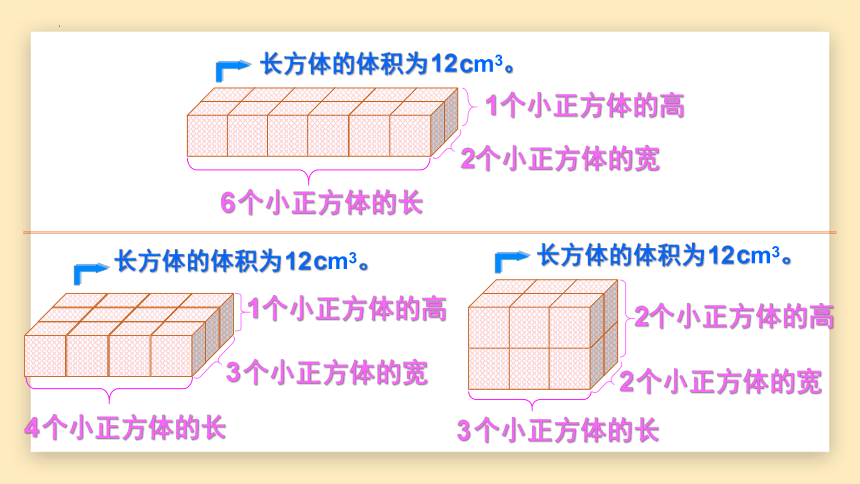
6个小正方体的长
2个小正方体的宽
1个小正方体的高
长方体的体积为12cm3。
4个小正方体的长
3个小正方体的宽
1个小正方体的高
长方体的体积为12cm3。
3个小正方体的长
2个小正方体的宽
2个小正方体的高
长方体的体积为12cm3。
我发现小正方体摆的长方体的形状不一样，但是长方体的体积都一样。
根据小实验，将数据做成了如下的表格：
长 宽 高 小正方体数量 长方体的体积
12cm 1cm 1cm 12个 12cm3
6cm 2cm 1cm 12个 12cm3
4cm 3cm 1cm 12个 12cm3
3cm 2cm 2cm 12个 12cm3
从表格中，你发现了什么？
长方体所含体积单位的个数就是长方体的体积。
12cm
1cm
1cm
6cm
2cm
1cm
4cm
3cm
1cm
3cm
2cm
2cm
12×1×1=12(cm3)
6×2×1=12(cm3)
4×3×1=12(cm3)
12cm
12cm3
12cm3
3×2×2=12(cm3)
12cm3
长方体的体积=
长×宽×高
长方体的体积正好等于长×
宽×高的积。
如果用字母V表示长方体的体积，用a、b、h分别表示长方体的长、宽、高，那么长方体的体积计算公式可以写成：
V = abh
想一想：根据长方体和正方体的关系，正方体的体积应该怎样计算？
正方体是长、宽、高都相等的长方体。
如果用字母V表示正方体的体积，用a表示它的棱长，那么正方体的体积计算公式可以写成：
正方体的体积=棱长×棱长×棱长
V = a · a · a
V = a3
a · a · a也可以写作“a3”，读作“a的立方”，表示3个a相乘。
随堂练习
1. 一个长方体包装箱，体积是48 dm3，长是4 dm，高是3 dm，宽是多少分米？
方法一
48÷4÷3
=12÷3
=4（dm）
方法二
解：设长方体的宽是x分米。
（4×3）x=48
12x=48
x=4
答：宽是4分米。
2. 判断。
（1）棱长是6 m的正方体的表面积和体积相等。
（ ）
正方体的表面积=棱长×棱长×6
6×6×6=216（m ）
正方体的体积=棱长×棱长×棱长
6×6×6=216（m ）
表面积和体积是两个不同的概念，单位不一样，不能比较大小。
×
（2） 一个正方体的棱长扩大为原来的2倍，它的体积就扩大为原来的8倍。 （ ）
1cm
1cm
1cm
假设棱长为1 cm，将棱长扩大2倍为：
1×2=2（cm）
正方体的体积=棱长×棱长×棱长
正方体原来的体积为：1×1×1=1（cm ）
正方体扩大后的体积为：2×2×2=8（cm ）
8÷1=8
√
课堂小结
长方体的体积＝长×宽×高
V＝abh
正方体的体积＝棱长×棱长×棱长
V＝ a3
长方体（或正方体）的体积=底面积×高
V = Sh
谢谢观看
人教版五年级数学下册

展开更多......

收起↑