资源简介

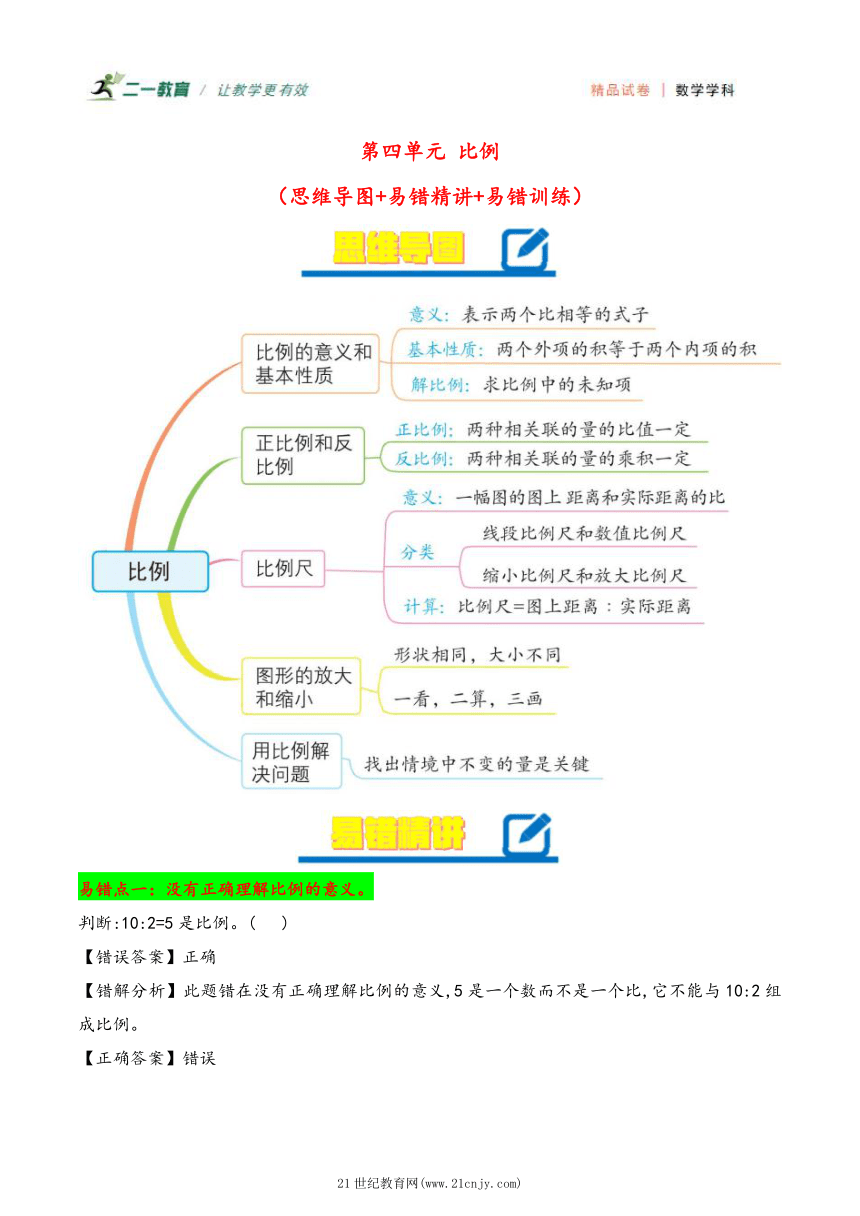
第四单元 比例
（思维导图+易错精讲+易错训练）
易错点一：没有正确理解比例的意义。
判断:10:2=5是比例。( )
【错误答案】正确
【错解分析】此题错在没有正确理解比例的意义,5是一个数而不是一个比,它不能与10:2组成比例。
【正确答案】错误
【易错例题一】下列各比中与能组成比例的是（ ）。
A．4∶2 B．2∶4 C．
【分析】表示两个比相等的式子叫做比例，求出各比的比值，找出和题中比值相等的选项即可。
【详解】＝＝
A．4∶2＝4÷2＝2；
B．2∶4＝2÷4＝；
C．＝＝。
故答案为：B
【点睛】掌握比例的意义、能够准确化简比，是解答题目的关键。
【易错例题二】用3、5、24和40你可以写出几个比例来？
【分析】根据比例的意义，表示两个比相等的式子叫做比例，把3、5、24和40这四个数中两两一组写成比，并求出比值，找出比值相等的比，组成比例即可；组成比例的两组比交换位置，可以组成新的比例；组成比例的两组比的前项和后项同时交换位置，也可以组成新的比例；比例的两内项交换位置或者两外项交换位置，也可以组成新的比例，列举出各比例即可。
【详解】3∶5＝3÷5＝
3∶24＝3÷24＝
3∶40＝3÷40＝
5∶24＝5÷24＝
5∶40＝5÷40＝
24∶40＝24÷40＝
可以组成的比例有：
3∶5＝24∶40；
24∶40＝3∶5；
5∶3＝40∶24；
40∶24＝5∶3；
3∶24＝5∶40；
5∶40＝3∶24；
24∶3＝40∶5；
40∶5＝24∶3
易错点二：对比例的基本性质理解不透彻。
判断:若5x=6y,则x :y=5∶6。( )
【错误答案】正确
【错解分析】这道题错在没有理解比例的基本性质。在改写比例时,x作外项,和x相乘的5一定也作外项。
【正确答案】错误
【易错例题一】如果比例的内项4增加8，那么外项3应该增加( )，比例才能成立。
【分析】根据比的基本性质，比的前项和后项同时乘或除以一个不为0的数，比值不变，据此填空即可。
【详解】（4＋8）÷4
＝12÷4
＝3
3×3－3
＝9－3
＝6
则外项3应该增加6，比例才能成立。
【点睛】本题考查比例的意义，明确两组比的比值相等，则它们可以组成比例是解题的关键。
易错点三：没有正确运用比例的基本性质解比例。
解比例
【错误答案】
【错解分析】解分数形式的比例时,没有分清楚哪两个数是外项,哪两个数是内项。
【正确答案】
【易错例题一】解方程。
2＋30%＝9.2 ∶＝∶
【分析】（1）先把30%化成0.3，然后根据等式的性质解方程，方程两边先同时减去0.3，再同时除以2，求出方程的解；
（2）先根据比例的基本性质把比例方程改写成＝×，然后方程两边同时除以，求出方程的解。
【详解】（1）2＋30%＝9.2
解：2＋0.3＝9.2
2＋0.3－0.3＝9.2－0.3
2＝8.9
2÷2＝8.9÷2
＝4.45
（2）∶＝∶
解：＝×
＝
÷＝÷
＝×
＝
【易错例题二】写出比例，并求出未知数。
光明小学为了预防新冠肺炎病毒传播，按照消毒液和水的比为1∶110的比例，配制消毒水进行教室消毒。现有y毫升的消毒液，需要水165毫升。
【分析】表示两个比相等的式子叫做比例，根据消毒液和水的比写出比例，再利用比例的基本性质求出未知数的值，据此解答。
【详解】y∶165＝1∶110
解：110y＝165
y＝165÷110
y＝1.5
答：1.5毫升的消毒液需要水165毫升。
【点睛】掌握比例的意义和解比例的方法是解答题目的关键。
易错点四：不能正确判断正比例关系。
判断:正方形的面积与边长成正比例关系。( )
【错误答案】正确
【错解分析】虽然正方形的面积与边长是两种相关联的量，但是正方形面积=边长,边长不是一个常量,所以正方形面积与边长不成正比例关边长系,应与边长的平方成正比例关系。
【正确答案】判断
【易错例题一】若a÷b＝8（a和b为非零自然数），则a和b的最大公因数是( )，a和b成( )比例关系。
【分析】两个数为倍数关系，则最大公因数是较小的数；判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定，如果是比值一定，就成正比例，如果是乘积一定，则成反比例。
【详解】因为a÷b＝8（a和b为非零自然数），所以a和b的最大公因数是b；
因为a÷b＝8（一定），商一定，所以a和b成正比例关系。
【点睛】熟练掌握求两个数最大公因数的方法以及判断两个相关联的量之间成什么比例的方法是解题的关键。
【易错例题二】如图表示的是一辆汽车所行驶的路程与时间的变化情况。
（1）图中的A点表示1小时行驶80千米，B点表示2小时行驶160千米，C、F两点分别表示什么？
（2）汽车行驶的路程与时间成什么比例？为什么？
（3）根据图像判断：这辆汽车2.5小时行驶了（ ）千米；行驶360千米需要（ ）小时。
【分析】（1）分别观察C、F点所对应的横轴上和纵轴上的数，即可求解；
（2）判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例；据此解答即可；
（3）根据速度×时间＝路程，即可求出这辆汽车2.5小时行驶了多少千米；根据时间＝路程÷速度，即可求出行驶360千米需要多少小时。
【详解】（1）C点表示3小时行驶240千米，F点表示6小时行驶480千米；
（2）路程与时间的比值是速度，速度是不变的，所以汽车行驶的路程与时间成正比例；
（3）2.5×80＝200（千米）
360÷80＝4.5（小时）
【点睛】本题主要考查根据统计图获取信息并解决问题的能力。
易错点五：不能正确判断反比例关系。
判断:把一条20 m长的绳子,剪去一部分,剪去的和剩下的成反比例关系。( )
【错误答案】正确
【错解分析】此题错在对剪去的和剩下的关系不清楚,两者是和一定、积不一定。
【正确答案】错误
【易错例题一】下面是关于正比例和反比例的描述，其中正确的是（ ）。
①正比例的图像是一条直线。②一个人的年龄和体重既不成正比例关系，也不成反比例关系。
③圆柱的底面积一定，体积和高成反比例关系。④路程一定，已走的路程和剩下的路程不成比例。
A．①②③ B．①②④ C．②③④ D．①③④
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。
【详解】①两种相关联的量中相对应的两个数的商一定，就成正比例关系，正比例的图像是一条过原点的直线；所以本选项正确。
②一个人的年龄和体重既不成正比例关系，也不成反比例关系；说法正确，因为人的体重与年龄不是相关联的量，所以不成比例。
③圆柱的体积÷高＝底面积（一定）所以，圆柱底面积一定，体积和高成正比例；本选项错误。
④因为：已走的路程＋剩下的路程＝两地的路程，是和一定，所以路程一定，已走的路程和剩下的路程不成比例；本选项正确。
所以，正确的是：①②④。
故答案为：B
【点睛】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断。
【易错例题二】某工厂有一批煤，每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
（1）判断每天烧煤的质量和可烧的时间是不是成反比例，并说明理由。
（2）如果该工厂平均每天烧煤的质量是5吨，那么这批煤可烧多少天？
【分析】（1）根据每天烧煤的质量和可烧的时间的乘积，结合反比例的意义判断。
（2）用这批煤的总质量除以每天烧煤的质量就是烧的天数。
【详解】（1）3×30＝6×15＝9×10＝15×6＝20×4.5＝90（一定）
每天烧煤的质量和可烧的时间的乘积一定，所以每天烧煤的质量和可烧的时间成反比例。
（2）30×3÷5
＝90÷5
＝18（天）
答：这批煤可烧18天。
【点睛】本题考查了成反比例关系的判定及根据成反比例关系解决问题，关键是对题目中数量关系的分析。
易错点六：没有理解比例尺的意义。
判断:一幅图的比例尺是1:5000 m。( )
【错误答案】正确
【错解分析】比例尺是一个比,是没有单位的。
【正确答案】错误
【易错例题一】学校的操场是一个长方形，长是90米，宽是60米，小聪想把它画在练习本上，比较合适的比例尺是（ ）。
A．1∶100 B．1∶1000 C．1∶10000 D．1∶1
【分析】根据图上距离＝实际距离×比例尺，先把单位换算成厘米后，把4个选项里的比例尺代入到数量关系中，分别求出练习本的长是多少，找出符合实际的答案即可。
【详解】90米＝9000厘米
A．9000×＝90（厘米），练习本有90厘米长，显然不符合实际；
B．9000×＝9（厘米），练习本有9厘米长，符合实际；
C．9000×＝0.9（厘米），练习本只有0.9厘米长，显然不符合实际；
D．9000×1＝9000（厘米），练习本有9000厘米长，显然不符合实际。
故答案为：B
【点睛】此题的解题关键是通过比例尺的运用，利用图上距离与实际距离之间的换算，求出结果，再进行判断。
【易错例题二】（1）市政府到儿童公园的实际距离是1050米，图中量得两地的图上距离为1.5厘米，这幅图的比例尺是（ ）。
（2）北山公园在市政府北偏东35°方向1750米处，在这幅地图上，市政府到北山公园的图上距离是（ ）厘米。
（3）在图中画出北山公园的位置。
【分析】（1）比例尺＝图上距离∶实际距离，把题中数据代入计算；
（2）根据“图上距离＝实际距离×比例尺”求出市政府到北山公园的图上距离；
（3）先把数值比例尺转化为线段比例尺，70000厘米＝700米，图上1厘米代表实际距离700米，再以市政府为观测点，在市政府北偏东35°方向截取1750÷700＝2.5个单位长度，标出角度，终点处标注北山公园，据此解答。
【详解】（1）1.5厘米∶1050米＝1.5厘米∶105000厘米＝1.5∶105000＝（1.5÷1.5）∶（105000÷1.5）＝1∶70000
（2）1750×＝0.025（米）
0.025米＝2.5厘米
所以，市政府到北山公园的图上距离是2.5厘米。
（3）
【点睛】掌握比例尺的意义以及图上距离和实际距离换算的方法是解答题目的关键。
易错点七：把图形放大或缩小时,改变了原图形的形状。
把下面图形按1:2缩小画在方格纸上。
【错误答案】
【错解分析】此题错在按1:2缩小时改变了原图形的形状。
【正确答案】
【易错例题一】把一个半径是3cm的圆按2∶1放大，放大后的圆的周长是（ ）cm。
A．12.56 B．18.84 C．28.26 D．37.68
【分析】根据图形放大与缩小的意义，按2∶1放大后的圆的半径是（3×2）cm，根据圆的周长计算公式“C＝”，即可计算出按2∶1放大后，得到的图形的周长。
【详解】3×2＝6（cm）
2×3.14×6
＝3.14×12
＝37.68（cm）
故答案为：D
【点睛】此题主要考查图形放大与缩小的意义以及圆的周长的计算方法。
【易错例题二】
（1）把三角形ABC按2∶1放大，画在如图的方格里。
（2）如果三角形ABC的顶点A用（3，4）表示，那么顶点B用（ ）表示，顶点C用（ ）表示。
（3）画出三角形ABC绕A点顺时针旋转90°的图形。
【分析】（1）把图形按照n∶1放大，就是将图形的每一条边放大到原来的n倍，放大后图形与原图形对应边长的比是n∶1。
（2）用数对表示位置时，通常把竖排叫列，横排叫行。一般情况下，确定第几列时从左往右数，确定第几行时从前往后数。表示列的数在前，表示行的数在后，中间用逗号“，”隔开，数对加上小括号。
（3）作旋转一定角度后的图形步骤：根据题目要求，确定旋转中心、旋转方向和旋转角；分析所作图形，找出构成图形的关键点；找出关键点的对应点：按一定的方向和角度分别作出各关键点的对应点；作出新图形，顺次连接作出的各点即可。
【详解】（1）把三角形ABC的三边同时扩大到原来的2倍，画在右边的方格图里。
（2）如果三角形ABC的顶点A用（3，4）表示，那么顶点B用（5，6）表示，顶点C用（6，4）表示。
（3）A点位置不变，确定出B点和C点绕A点顺时针旋转90°后的位置，再依次连线。
【点睛】图形放大或缩小是指对应边放大或缩小；用有顺序的两个数表示出一个确定的位置就是数对；决定旋转后图形的位置的要素：一是旋转中心或轴，二是旋转方向（顺时针或逆时针），三是旋转角度。
易错点八：用比例解决问题时没有理清数据间的关系。
某工程队修一条公路,6天铺了228 m。照这样计算,还要用12天完成全部的工程,这条公路一共长多少米
【错误答案】
【错解分析】解法一错在两个相关联的量中,错把12天看成总天数。解法二错在不理解等量关系,把天数和铺的米数看成反比例关系。
【正确答案】
【易错例题一】甲、乙两个圆柱形容器，底面积比为6∶4，甲容器中水深18厘米，乙容器中水深12厘米，再往两个容器中注入同样多的水，使得两个容器中水一样深，这时水深( )厘米。
【分析】根据体积相等时，圆柱的底面积和高成反比，底面积比为6：4，那么注入同体积的水的深度比是4：6，可设这时水深为x厘米，根据水的深度比，列出方程即可解答。
【详解】解：设这时水深为x厘米。
【点睛】本题主要考查圆柱的体积公式的灵活运用，列出方程解决问题是比较直观的方法。
【易错例题二】某物流公司将120t蔬菜运往上海，如果要一次把所有货物全部运出，每辆车的载质量与所需车辆数量如下表。
每辆车的载质量/t 2.5 3 5 10
所需车辆数量/辆 48 40 24 12
（1）每辆车的载质量与所需车辆数量成（ ）比例关系。
（2）如果用15辆相同的车来运，每辆车的载质量是多少吨？
【分析】（1）蔬菜的总质量不变，说明每辆车的载质量与所需车辆数量乘积不变，则每辆车的载质量与所需车辆数量成反比例关系；
（2）用蔬菜质量除以所需车辆数量，求出每辆车的载质量即可。
【详解】（1）每辆车的载质量与所需车辆数量成反比例关系；
（2）（吨）
答：每辆车的载质量是8吨。
【点睛】本题考查反比例，解答本题的关键是掌握成反比例关系的概念。
一、选择题
1．下面4个数中，不能与“4，20，15”组成比例的是（ ）。
A．3 B． C．16 D．75
2．小宜在方格纸上画了一个“T”字图案（如下图），他若将该图案的高度和宽度增加一倍后是图（ ）。
A． B． C． D．
3．有两个相关联的量，它们的关系如图。这两个相关联的量可能是（ ）。
A．订阅《智力数学》的总价与本数
B．路程一定时，行驶速度与行驶时间
C．圆的面积与它的半径
D．一袋大米的质量一定，吃掉的大米质量与剩下的大米质量
4．一个长方形的面积是13平方厘米，按4∶1的比例尺放大后它的面积是（ ）。
A．52平方厘米 B．104平方厘米
C．208平方厘米 D．169平方厘米
5．一幅图的比例尺是1∶20000，下面说法错误的是（ ）。
A．图上距离是实际距离的 B．图上1cm表示实际距离200m
C．图上距离的200倍就是实际距离 D．这幅图中，图上距离与实际距离成正比例
6．如下图，平行四边形a边上的高为b，c边上的高为d。根据这些信息，下列式子成立的有（ ）个。

①a∶c＝b∶d ②a∶c＝d∶b ③ ④
A．1 B．2 C．3 D．4
二、填空题
7．社区准备修建一个长为200米，宽为150米的公园，画在比例尺是1∶5000的图纸上，则图上的宽为( )厘米。
8．在比例尺是1∶5000000的图纸上，量得A城与B城之间的距离是36厘米，两城之间的实际距离是( )千米。如果某班航机以900千米／时的速度从A城往西南方向飞行到达B城，那么该航机要以相同速度从B城飞回A城需往( )方向飞行( )时。
9．一个长方形的周长是24分米，长和宽都是质数，这个长方形的面积是( )平方分米。将这个长方形按1∶2缩小后，缩小后的面积是原来长方形面积的( )。
10．小莉用水和蜂蜜为一家人分别调制了四杯蜂蜜水，蜂蜜和水的配比情况如下表。
四杯蜂蜜水的配比情况表：
第一杯 第二杯 第三杯 第四杯
蜂蜜/mL 12 11 10 14
水/mL 60 44 60 70
把最甜的一杯给弟弟，弟弟喝的是第( )杯蜂蜜水，你判断的理由是( )。同样甜的两杯给爸爸和妈妈，请你根据这两杯蜂蜜水的配比情况写出一个比例是( )。
11．弹簧秤可以用来称物体的质量。悬挂物体的质量不同，弹簧伸长的长度也不同，有一个弹簧秤最多能称6千克重的物体。先观察下表，再填空。
悬挂物体的质量（千克） 1 2 3 …
弹簧伸长的长度（厘米） 3 6 9 …
如果悬挂5千克的物体，那么弹簧伸长的长度是( )厘米如果弹簧伸长的长度是7.5厘米，那么悬挂物体的质量是( )千克。
12．有一种弹簧秤，秤上挂上物品（质量在100克以内）时，物品的质量与弹簧伸长的长度情况如图所示：

(1)如果挂40克重物，弹簧伸长的长度是( )厘米；当弹簧伸长的长度是4厘米时，所挂物品的质量是( )克。
(2)弹簧伸长的长度与所挂物品的质量成( )比例关系。
三、判断题
13．比例尺1∶1表示图上距离和实际距离相等。( )
14．在9∶3＝2.7∶0.9中，3和2.7是比例的内项，9和0.9是比例的外项。( )
15．如果高铁行驶速度保持不变，则它所行驶的路程与所用时间成反比例。( )
16．比例尺1∶500是指图上距离1厘米表示实际距离500千米。( )
四、计算题
17．解比例。
（1）x∶25＝1.2∶7.5 （2） （3）
五、作图题
18．按要求在方格纸上用铅笔画图。

（1）先画出图形A的对称轴，再画出把图形A向右平移4格后得到的图形B。
（2）画出把图形A按2∶1的比例放大得到的图形C。
（3）画出三角形绕O点顺时针旋转180°后得到的图形E。
六、解答题
19．李叔叔承包了两块水稻田，面积分别为0.5公顷和0.8公顷。秋收时，两块水稻田的产量分别为3.75吨和6吨。两块水稻田的产量与面积之比，是否可以组成比例？如果可以组成比例，指出比例的内项和外项。
20．西安钟楼是中国现存钟楼中形制最大、保存最完整的一座钟楼，总高36米。某展馆设计制作了钟楼的模型，模型的高度与实际高度的比是1∶50。模型的高度是多少米？（用比例解）
21．在比例尺是1∶8000000的地图上量的甲地到乙地的距离是14厘米。一列火车3小时行驶了420千米，照这样的速度，这列火车上午10时40分从甲地出发，何时能到达乙地？
22．广州塔高600米，是目前世界第一高的电视塔。王师傅制作了广州塔的模型，模型高度与实际高度的比是1∶2000。模型的高度是多少米？（列比例解决）
23．甲、乙两地相距520千米。一辆汽车从甲地出发开往乙地，前3小时行驶了240千米。照这样的速度，到达乙地一共需要多少小时？（用比例解）
24．开车从安阳到北京要行驶约500千米。一辆汽车从安阳出发前往北京，5小时行了全程的。照这样的速度，到达北京共需要多少小时？
25．操作题。（用铅笔和直尺画实线完成操作）

（1）在方格纸上依次标出点，，，顺次连接A、B、C、A，画成的图形是（ ）。
（2）把上面图形按2∶1放大，画出放大后的图形。
（3）将放大前的图形以AC为轴旋转一周，可以得到一个（ ），若每个方格的边长为1厘米，则这个图形的体积为（ ）立方厘米。
26．如图是博物馆附近的平面图。
（1）这幅图的数值比例尺是（ ）。
（2）停车场在博物馆的（ ）方向，实际距离是（ ）米。
（3）歌剧院位于博物馆南偏西35°方向800米处，在图中标出歌剧院的位置。
（4）小芳从歌剧院走到博物馆，向（ ）偏（ ）（ ）°方向走（ ）米就可以到达。
27．丽丽、媛媛、君君都看了《故事大全》这本书。
（1）填写每人看完这本书需要的天数。
丽丽 媛媛 君君
每天看的页数 5 8 10
看的天数 24
（2）每天看的页数和看的天数之间有什么关系？
（3）照这样的速度看6天，他们各看了多少页，还剩多少页？把结果填在表中。
丽丽 媛媛 君君
已看的页数
剩下的页数
已看的页数和剩下的页数成比例吗？为什么？
参考答案
1．C
【分析】根据比例的基本性质：两外项之积等于两内项之积；据此判断每个选项即可。
【详解】A．3×20＝60
4×15＝60
3能与“4，20，15”组成比例；
B．4×20＝80
×15＝80
能与“4，20，15”组成比例；
C．4×20＝80
15×16＝240
80不等于240，16不能与“4，20，15”组成比例；
D．4×75＝300
20×15＝300
75能与“4，20，15”组成比例。
故答案为：C
2．A
【分析】原来“T”字图案上部分的宽度是3小格，下部分的宽度是1小格，增加一倍后，上部分的宽度从3小格增加为6小格；下部分的宽度从1小格增加为2小格；原来图案的高度是3小格，增加一倍后，高度从3小格增加为6小格，据此判断。
【详解】将原来图案的高度和宽度增加一倍后的图是。
故答案为：A
3．A
【分析】正比例关系的图像是一条直线，由图可以看出这两个量成正比例关系，判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定，如果是比值一定，就成正比例，如果是乘积一定，则成反比例。
【详解】A．《智力数学》订阅的总价÷本数＝单价（一定），商一定，所以《智力数学》订阅的总价和本数成正比例；
B．行驶速度×时间＝总路程（一定），是对应的乘积一定，所以速度和所用的时间成反比例；
C．因为圆的面积÷它的半径＝π×半径（不一定），是圆的面积与它的半径的比值不一定，既不符合正比例的意义，也不符合反比例的意义；
D．因为吃掉的大米质量＋剩下的质量＝大米的总量（一定），既不符合正比例才意义，也不符合反比例的意义；
故答案为：A
4．C
【分析】把长方形按4∶1的比例尺进行放大，即把长方形的各个边长都扩大到原来的4倍；因为长方形的面积＝长×宽，再结合积的变化规律，一个因数乘4，另一个因数也乘4，则积应乘4×4＝16，据此进行并选择即可。
【详解】13×（4×4）
＝13×16
＝208（平方厘米）
则一个长方形的面积是13平方厘米，按4∶1的比例尺放大后它的面积是208平方厘米。
故答案为：C
5．C
【分析】比例尺的意义：图上距离与实际距离的比叫做比例尺。根据比例尺的意义可知，比例尺1∶20000表示图上1cm相当于实际距离20000cm，也就是实际距离是图上距离的20000倍。
判断两种相关联的量之间成什么比例，就看这两个量是对应的比值（商）一定，还是对应的乘积一定；如果是比值（商）一定，这两种相关联的量成正比例；如果是乘积一定，这两种相关联的量成反比例。
【详解】A．一幅图的比例尺是1∶20000，图上距离是实际距离的，原题说法正确；
B．20000cm＝200m，图上1cm表示实际距离200m，原题说法正确；
C．比例尺1∶20000表示图上距离的20000倍就是实际距离，原题说法错误；
D．图上距离∶实际距离＝比例尺（一定），比值一定，则这幅图中，图上距离与实际距离成正比例，原题说法正确。
故答案为：C
6．C
【分析】根据平行四边形面积公式：面积＝底×高；平行四边形面积：ab＝cd，再根据比例的基本性质：比例的两个内项之积等于两个外项之积，据此逐项分析，即可解答。
【详解】ab＝cd
①a∶c＝b∶d；ad＝cb，不成立
②a∶c＝d∶b；ab＝cd，成立；
③＝；ab＝cd，成立；
④＝；ab＝cd，成立。
②③④成立。共有3个。
如下图，平行四边形a边上的高为b，c边上的高为d。根据这些信息，下列式子成立的有3个。
故答案为：C
【点睛】熟练掌握平行四边形的面积公式以及比例的基本性质是解答本题的关键。
7．3
【分析】先根据进率“1米＝100厘米”，把宽150米换算成15000厘米；
再根据“图上距离＝实际距离×比例尺”，求出图上的宽。
【详解】150米＝15000厘米
15000×＝3（厘米）
则图上的宽为3厘米。
8． 1800 东北 2
【分析】根据实际距离＝图上距离÷比例尺，用36÷即可求出两城之间的实际距离，再将单位换算成千米；方向和距离两个条件才能确定物体的位置，根据位置的相对性，可知两处位置观测点不同，它们的方向相反，角度相等；根据时间＝路程÷速度，用两城的距离除以900千米／时，即可求出返回时需要多少时间。
【详解】36÷
＝36×5000000
＝180000000（厘米）
180000000厘米＝1800千米
1800÷900＝2（小时）
两城之间的实际距离是1800千米。
该航机要以相同速度从B城飞回A城需往东北方向飞行2时。
9． 35
【分析】根据长方形的周长＝（长＋宽）×2，用24÷2即可求出长方形长与宽的和，也就是12分米，然后将12分别拆成2个数相加，符合长、宽都是质数的只有12＝5＋7，所以长是7分米，宽是5分米；长方形按1∶2缩小，则长和宽分别缩小到原来的，用7÷2即可求出现在的长，用5÷2即可求出现在的宽，最后根据长方形的面积＝长×宽，分别求出缩小前后长方形的面积，再用缩小后的面积除以缩小前的面积，即可求出缩小后的面积是原来长方形面积的几分之几。
【详解】24÷2＝12（分米）
长和宽都是质数，
所以12＝5＋7
长是7分米，宽是5分米；
5÷2＝2.5（分米）
7÷2＝3.5（分米）
5×7＝35（平方分米）
2.5×3.5＝8.75（平方分米）
8.75÷35＝
一个长方形的周长是24分米，长和宽都是质数，这个长方形的面积是35平方分米。将这个长方形按1∶2缩小后，缩小后的面积是原来长方形面积的。
【点睛】本题主要考查了长方形周长和面积公式的灵活应用、质数的认识、图形的缩小等，要熟练掌握每个知识点。
10． 二 第二杯蜂蜜和水的比值最大 12∶60＝14∶70
【分析】将蜂蜜的质量除以水的质量，求出每杯蜂蜜水中蜂蜜和水的比值。比值越大，蜂蜜水越甜；
比值相等的两杯蜂蜜水同样甜。比值相等的两个比可以组成一个比例。据此，写出一个比例即可。
【详解】12÷60＝0.2
11÷44＝0.25
10÷60＝
14÷70＝0.2
0.25＞0.2＞
所以弟弟喝的是第二杯蜂蜜水，理由是第二杯蜂蜜和水的比值最大（答案不唯一）。
同样甜的两杯是第一杯和第四杯，写成的比例可以是12∶60＝14∶70（答案不唯一）。
11． 15 2.5
【分析】观察表格数据可知数量关系：弹簧伸长的长度＝悬挂物体的质量×3，将5千克代入数量关系求出弹簧伸长的长度即可；已知弹簧伸长的长度是7.5厘米，用7.5除以3即可求出悬挂物体的质量，据此解答。
【详解】5×3＝15（厘米）
7.5÷3＝2.5（千克）
所以，悬挂5千克的物体，那么弹簧伸长的长度是15厘米，如果弹簧伸长的长度是7.5厘米，那么悬挂物体的质量是2.5千克。
【点睛】此题考查了小数除法的运用，关键能够结合条件找出数量关系再解答；也可以用正比例的知识解答。
12．(1) 8 20
(2)正
【分析】（1）观察图示，第一个空，找到横轴40克对应的弹簧伸长的数据即可；第二个空，找到竖轴4厘米对应的横轴质量即可。
（2）根据x÷y＝k（一定），x和y成正比例关系，进行分析。
【详解】（1）如果挂40克重物，弹簧伸长的长度是8厘米；当弹簧伸长的长度是4厘米时，所挂物品的质量是20克。
（2）10÷2＝5、20÷4＝5、30÷6＝5……
弹簧伸长的长度与所挂物品的质量成正比例关系。
【点睛】关键是理解正比例的意义，正比例图像是一条经过原点的直线。
13．√
【分析】根据比例尺的意义可知，图上距离和实际距离的比，叫做这幅图的比例尺；即：图上距离∶实际距离＝图上距离÷比例尺；据此解答。
【详解】由分析可得：图上距离和实际距离的比叫做比例尺；所以比例尺1∶1，说明图上距离和实际距离相等，原题说法正确。
故答案为：√
14．√
【分析】组成比例的四个数，叫做比例的项，两端的两项叫做比例的外项，中间的两项叫做比例的内项。
【详解】3和2.7是中间的两项，即为比例的内项，9和0.9是两端的两项，即为是比例的外项，原题目说法正确；
故答案为：√
15．×
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。根据路程÷时间＝速度，速度不变，也就是路程和时间的比值不变，则路程和时间成正比例。
【详解】根据分析可知，如果高铁行驶速度保持不变，则它所行驶的路程与所用时间成正比例。原题干说法错误。
故答案为：×
【点睛】本题考查了正比例、反比例的意义和辨识，掌握相关判别方法是解答本题的关键。
16．×
【分析】一幅图的图上距离与实际距离的比，叫作这幅图的比例尺，比例尺＝图上距离∶实际距离，比例尺是1∶500表示图上1厘米代表实际距离500厘米，据此解答。
【详解】分析可知，比例尺1∶500是指图上距离1厘米表示实际距离500厘米。
故答案为：×
【点睛】本题主要考查比例尺的认识，掌握比例尺的意义是解答题目的关键。
17．（1）x＝4；（2）x＝3.8；（3）x＝7.5
【分析】（1）根据比例的基本性质，把式子转化为7.5x＝1.2×25，再化简方程，最后根据等式的性质，方程两边同时除以7.5即可；
（2）根据比例的基本性质，把式子转化为0.85x＝1.7×1.9，再化简方程，最后根据等式的性质，方程两边同时除以0.85即可；
（3）根据比例的基本性质，把式子转化为x＝×10，再化简方程，最后根据等式的性质，方程两边同时除以即可。
【详解】（1）x∶25＝1.2∶7.5
解：7.5x＝1.2×25
7.5x＝30
7.5x÷7.5＝30÷7.5
x＝4
（2）
解：0.85x＝1.7×1.9
0.85x＝3.23
0.85x÷0.85＝3.23÷0.85
x＝3.8
（3）
解：x＝×10
x＝2.5
x÷＝2.5÷
x＝2.5×3
x＝7.5
18．见详解
【分析】（1）取这个等腰梯形上底和下底的中点，画出一条直线，即图形A的对称轴；将图形A的各边均向右平移4格，画出平移后的图形B；
（2）按2∶1的比例放大，即将图形的各边扩大到原来的2倍，据此画出图形C；
（3）点O不动，将三角形各边绕点O顺时针旋转180°，画出旋转后的图形E。
【详解】（1）如图：

（2）2×2＝4
4×2＝8
如图：

（3）如图：

【点睛】本题考查了图形的运动，掌握平移、旋转以及图形的放大的作图方法是关键。
19．可以组成比例，3.75∶0.5＝6∶0.8，其中3.75和0.8是外项，0.5和6是内项。
【分析】表示两个比相等的式子叫做比例。组成比例的四个数，两端的两项叫作比例的外项，中间的两项叫作比例的内项。
【详解】第一块水稻田的产量与面积之比是3.75∶0.5，比值是7.5；第二块水稻田的产量与面积之比是6∶0.8，比值是7.5；所以可以组成比例为3.75∶0.5＝6∶0.8。其中3.75和0.8是外项，0.5和6是内项。（答案不唯一）
20．0.72米
【分析】根据题意可知，钟楼模型的高度∶钟楼实际的高度＝1∶50，据此列出比例方程，并求解。
【详解】解：设模型的高度是米。
∶36＝1∶50
50＝36×1
＝36÷50
＝0.72
答：模型的高度是0.72米。
【点睛】本题考查比例的应用，从题目中找到等量关系，根据等量关系列出方程。
21．18时40分
【分析】已知甲地到乙地的图上距离和比例尺，根据“实际距离＝图上距离÷比例尺”以及进率“1千米＝100000厘米”，求出甲、乙两地的实际距离；
已知一列火车3小时行驶了420千米，根据“速度＝路程÷时间”，求出这列火车的速度；再根据“时间＝路程÷速度”，求出这列火车从甲地到乙地需要的时间，最后加上火车从甲地的出发时刻，即可求出火车到达乙地的时刻。
【详解】甲、乙两地的实际距离：
14÷
＝14×8000000
＝112000000（厘米）
112000000厘米＝1120千米
火车的速度：420÷3＝140（千米/时）
火车从甲地到乙地需要的时间：1120÷140＝8（小时）
到达乙地的时刻：10时40分＋8小时＝18时40分
答：18时40分能到达乙地。
22．0.3米
【分析】由题意可知，设模型的高度是x米，再根据模型的高度与实际的高度比是1∶2000，列出比例解比例即可。
【详解】解：设模型的高度是x米。
x∶600＝1∶2000
2000x＝600×1
2000x＝600
2000x÷2000＝600÷2000
x＝0.3
答：模型的高度是0.3米。
23．6.5小时
【分析】根据速度＝路程÷时间；根据题意，由于汽车的速度不变，前3小时行驶的速度与从甲地到乙地行驶的速度相等，设到达乙地一共需要x小时，列比例：240∶3＝520∶x，解比例，即可解答。
【详解】解：设到达乙地一共需要x小时。
240∶3＝520∶x
240x＝520×3
240x＝1560
x＝1560÷240
x＝6.5
答：到达乙地一共需要6.5小时。
24．6.25小时
【分析】把全长看作单位“1”，根据分数乘法的意义，用500×即可求出5小时行驶的路程，根据路程÷时间＝速度，速度一定，路程和时间成正比例，设到达北京共需要x小时，列比例为：500∶x＝（500×）∶5，然后解出比例即可。
【详解】解：设到达北京共需要x小时。
500∶x＝（500×）∶5
500∶x＝400∶5
400x＝500×5
400x＝2500
x＝2500÷400
x＝6.25
答：到达北京共需要6.25小时。
【点睛】本题主要考查了正比例的应用，掌握解比例的方法是解答本题的关键。
25．（1）作图见详解；直角三角形
（2）见详解
（3）圆锥；50.24
【分析】（1）用数对表示位置时，通常把竖排叫列，横排叫行。一般情况下，确定第几列时从左往右数，确定第几行时从前往后数。表示列的数在前，表示行的数在后，中间用逗号“，”隔开，数对加上小括号。
据此标出各点，顺次连接，可以发现是个直角三角形。
（2）把图形按照n∶1放大，就是将图形的每一条边放大到原来的n倍，放大后图形与原图形对应边长的比是n∶1，据此画出放大后的图形。
（3）以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。圆锥的底面半径4厘米，高3厘米，根据圆锥体积＝底面积×高÷3，求出体积即可。
【详解】（1）（2）如图：

（1）顺次连接A、B、C、A，画成的图形是直角三角形。
（3）3.14×42×3÷3
＝3.14×16×3÷3
＝50.24（立方厘米）
将放大前的图形以AC为轴旋转一周，可以得到一个圆锥，若每个方格的边长为1厘米，则这个图形的体积为50.24立方厘米。
【点睛】关键是掌握用数对表示位置的方法，熟悉圆锥特征，掌握并灵活运用圆锥体积公式，图形放大或缩小是指对应边放大或缩小。
26．（1）1∶20000；（2）正北；600；
（3）见详解
（4）北；东；35；800
【分析】（1）由图可知，图上1厘米表示实际距离200米，比例尺＝图上距离∶实际距离；
（2）根据图中上北下南，左西右东，停车场在博物馆的正北方向，测量图上为3厘米，那么实际距离就是：3×200＝600米；
（3）歌剧院位于博物馆南偏西35°方向800米处，也就是从正南向西画35°长度为800÷2＝400（厘米）的线段，标上数据、名称即可；
（4）小芳从歌剧院走到博物馆，以歌剧院为观测点，向北偏东35°方向走800米就可以到达。
【详解】（1）1cm∶200m＝1∶20000或
这幅图的数值比例尺是：1∶20000或。
（2）3×200＝600（米）
停车场在博物馆的（正北）方向，实际距离是（600）米。
（3）作图如下：
（4）小芳从歌剧院走到博物馆，向（北）偏（东）（35）°方向走（800）米就可以到达。
【点睛】掌握图上距离、实际距离、比例尺之间的关系以及根据方向、角度、距离确定位置是解题的关键。
27．（1）15；12；
（2）成反比例关系；
（3）填表见详解；不成比例，因为已看的页数和剩下的页数的积和商（比值）都不是一定的，而是和一定。
【分析】（1）根据丽丽每天看的页数和看的天数，计算全书的页数，从而求出媛媛、君君看的天数。据此填表即可。
（2）相关联的两个变量，比值一定，成正比例；相关联的两个量，乘积一定，成反比例；据此可知：每天看的页数和看的天数的积（全书的页数）一定，所以每天看的页数和看的天数成反比例关系。
（2）照原来的速度，分别计算每人已看的页数和剩下的页数，发现已看的页数和剩下的页数的和一定，所以已看的页数和剩下的页数不成比例。
【详解】（1）24×5＝120（页）
120÷8＝15（天）
120÷10＝12（天）
填表如下：
丽丽 媛媛 君君
每天看的页数 5 8 10
看的天数 24 15 12
（2）全书的页数是一定的；
答：由于每天看的页数和看的天数的积（全书的页数）一定，所以每天看的页数和看的天数成反比例关系。
（3）5×6＝30（页）
120－30＝90（页）
8×6＝48（页）
120－48＝72（页）
10×6＝60（页）
120－60＝60（页）
填表如下：
丽丽 媛媛 君君
已看的页数 30 48 60
剩下的页数 90 72 60
观察发现，已看的页数和剩下的页数的和一定，所以已看的页数和剩下的页数不成比例。
答：已看的页数和剩下的页数不成比例，因为已看的页数和剩下的页数的积和商（比值）都不是一定的，而是和一定。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑