资源简介

中小学教育资源及组卷应用平台
模拟试题预测练
2025年中考数学三轮复习备考
一、单选题
1．以下各数中绝对值最小的数是（ ）
A．0 B． C．2 D．
2．相关报告显示，2025年，中国人形机器人市场规模预计达亿元，占全球约．其中亿用科学记数法表示为（ ）
A． B． C． D．
3．计算的结果是（ ）
A． B． C． D．
4．如图是一个长方体切去一部分后得到的几何体，切点，是原长方体棱的中点，其主视图为（ ）
A． B． C． D．
5．不等式组的解集在数轴上表示正确的是（ ）
A． B．
C． D．
6．已知直线经过第一象限，则下列各点中一定在直线上方的是（ ）
A． B． C． D．
7．如图，在中，，为边上一点，连接，，，将沿折叠，点恰好落在上的点处，则的长为（ ）
A．5 B．4.5 C．4 D．3
8．人工智能（AI），是新一轮科技革命和产业变革的重要驱动力量，是研究、开发用于模拟、延伸和扩展人类智能的理论、方法、技术及应用系统的一门新兴的技术科学．小明和小丽两位同学计划利用假期，通过智慧课堂学习大数据技术、信息安全和物联网工程三门课程中的任意一门课程，则两人选中信息安全和大数据技术的概率为（ ）
A． B． C． D．
9．已知实数，，满足，，则下列结论正确的是（ ）
A．， B．， C． D．
10．如图，在四边形中，，，，为边上一点（不与点，重合），连接，，，且，，为的中点，连接，，则下列结论错误的是（ ）
A．若，则
B．若，则四边形的周长为33.6
C．的面积最大为25
D．的面积恒为12
二、填空题
11．与最接近的整数是 ．
12．写一个图象经过第二、四象限的正比例函数的表达式：
13．计算的结果是 ．
14．如图，为了测量某电子厂的高度，小明用高的测量仪测得顶端A的仰角为，小军在小明的前面处用高的测量仪测得顶端的仰角为，则电子厂的高度约是 （参考数据：，，．
15．如图，已知，均为等腰直角三角形，，为的中点，的延长线交线段于点，连接．若，，则 ．
16．已知抛物线（为常数，）经过点，，且，则下列四个结论：①；②；③若方程有两个不相等的实数根（且），则；④若，抛物线过点，且，则．其中正确的结论是 （填序号）．
三、解答题
17．（1）计算：
（2）化简：
18．求不等式组的整数解．
19．如图，中，平分，为延长线上一点，于，已知，，
(1)的度数为___________；
(2)求的度数．
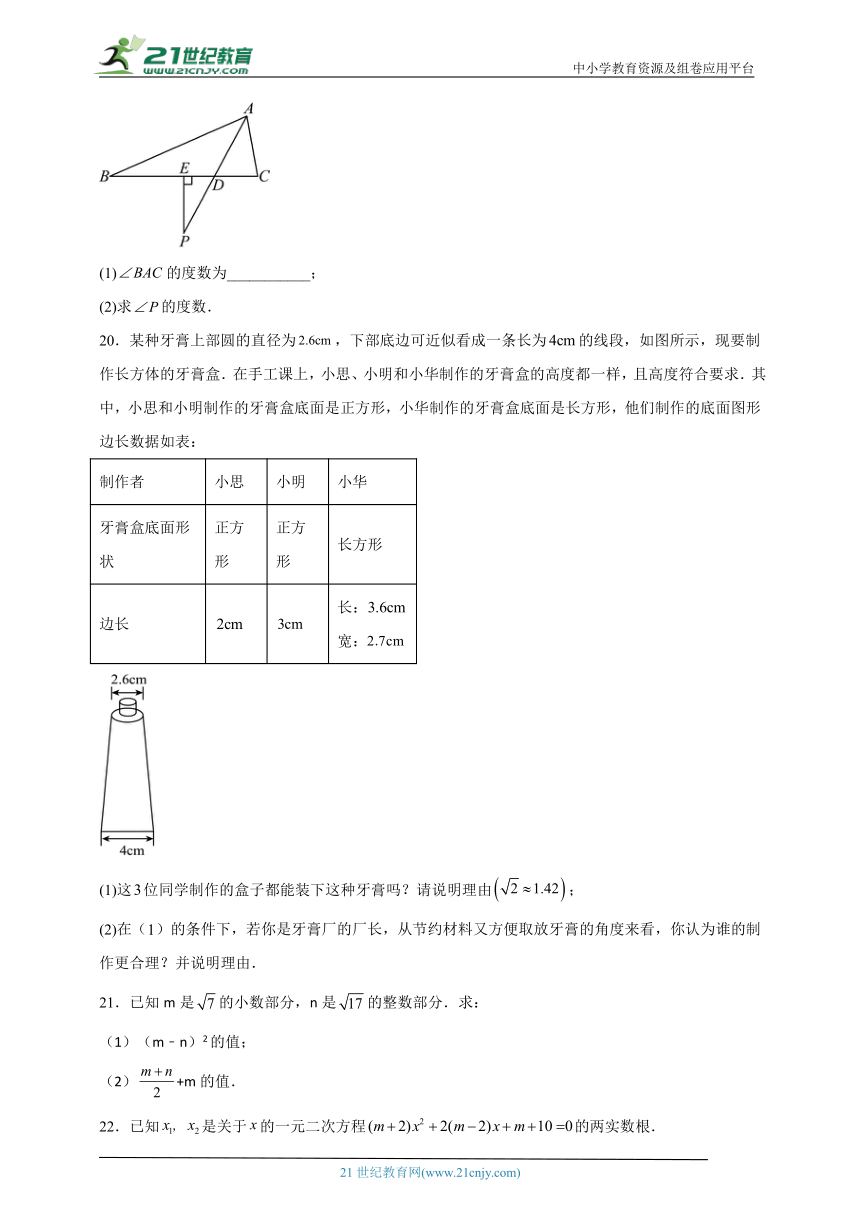
20．某种牙膏上部圆的直径为，下部底边可近似看成一条长为的线段，如图所示，现要制作长方体的牙膏盒．在手工课上，小思、小明和小华制作的牙膏盒的高度都一样，且高度符合要求．其中，小思和小明制作的牙膏盒底面是正方形，小华制作的牙膏盒底面是长方形，他们制作的底面图形边长数据如表：
制作者 小思 小明 小华
牙膏盒底面形状 正方形 正方形 长方形
边长 长： 宽：
(1)这位同学制作的盒子都能装下这种牙膏吗？请说明理由；
(2)在（）的条件下，若你是牙膏厂的厂长，从节约材料又方便取放牙膏的角度来看，你认为谁的制作更合理？并说明理由．
21．已知m是的小数部分，n是的整数部分．求：
（1）（m﹣n）2的值；
（2）+m的值．
22．已知是关于的一元二次方程的两实数根．
(1)求的取值范围；
(2)已知等腰的底边，若恰好是另外两边的边长，求这个三角形的周长．
(3)阅读材料：若三边的长分别为，那么可以根据海伦-秦九韶公式可得： ，其中，在（2）的条件下，若和的角平分线交于点，根据以上信息，求的面积．
23．如图，为的直径，为上一点，，交于点，且，连接．
(1)求证：是的切线；
(2)为上一点，连接，若，，，求的半径．
24．（一）、问题背景：
数学活动课上，老师拿出一个由五连格边长为1的正方形连成的L形教具，将它放入一个的直角三角形中，，，如图1顶点D，E，F，G刚好落在三边上，请求出此直角三角形的面积．
（二）、问题提出与解决：（以下问题二选一解答）
（1）小颖同学受到启发，将此教具放入如图的直角坐标系中，顶点A，B，C分别落在坐标轴上，提出问题：如图2，如果反比例函数图像经过顶点D，试求出反比例解析式．
（2）小明同学也受到启发，画了一个圆，如图3，将此教具放入圆内，使圆经过其顶点A，B，C，提出问题：怎么算出圆的面积
25．已知，我们不妨约定：当自变量x满足：时，函数值y恰好满足：，此时我们就说该函数是“星联函数”，“”的值叫做该“星联函数”的“星联距离”，根据约定，解答下列问题：
(1)当时，试判断下列函数哪些是“星联函数”？是“星联函数”的在括号内划“√”，不是“星联函数”的在括号内划“×”；
①（ ）；②（ ）；③（ ）．
(2)若当时，一次函数（）是“星联函数”，试求出该一次函数的解析式，并求出该函数的“星联距离”；
(3)当时，“星联函数”解析式为，求该函数的“星联距离”．
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D B B A D D C
1．A
【分析】本题主要考查了绝对值的求解方法，熟练求解各数的绝对值并进行绝对值的大小比较是解决本题的关键．
根据题意，将各选项的绝对值求出后进行对比，选择最小的即可．
【详解】解：，，，，
∵
∴绝对值最小的数是0，
故选：A．
2．C
【分析】本题考查了科学记数法，科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原来的数，变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正数；当原数的绝对值时，是负数，确定与的值是解题的关键．
【详解】解：亿．
故选：C．
3．C
【分析】本题考查了负整数指数幂，根据负整数指数幂的运算法则，，进行计算即可求解．
【详解】解：
故选：C．
4．D
【分析】本题考查三视图．熟练掌握三视图的确定方法，是解题的关键．注意，存在看不见的用虚线表示．从正面看，确定主视图即可．
【详解】
解：几何体的主视图为：
故选：D．
5．B
【分析】本题考查解一元一次不等式组及在数轴上表示不等式的解集，正确得出各不等式的解集，熟练掌握解集的表示方法是解题关键．注意：表示解集时，带等号的要用实心点表示，不带等号的用空心点表示．分别求出两个不等式的解集，再找出两个解集的公共部分得出不等式组的解集，根据解集在数轴上表示方法即可得答案．
【详解】，
解不等式①得：，
解不等式②得：，
∴不等式的解集为：，
∴不等式组的解集在数轴上表示如下：
故选：B．
6．B
【分析】本题考查了一次函数的性质，根据题意得出直线经过第一、三、四象限，进而可得第二象限的点一定在直线上方，即可求解．
【详解】解：∵直线经过第一象限，
∴，
∵
∴直线经过第一、三、四象限，
∴第二象限的点一定在直线上方
∴在直线上方
故选：B．
7．A
【分析】本题考查了平行四边形的性质、折叠的性质、等角对等边．根据平行四边形的性质和折叠的性质可求出，，得到，据此求解即可．
【详解】解：∵，
∴，
∴，
∵将沿折叠，点恰好落在线段上的点处，
∴，，
∴，
∴，
∴，
故选：A．
8．D
【分析】本题考查了用列表法或画树状图法求概率，掌握求概率的方法是解题的关键．根据列表法求概率，即可求解．
【详解】解：设大数据技术、信息安全和物联网工程三门课程分别为，列表如下
共有种等可能结果，其中符合题意的有2种，
则两人选中信息安全和大数据技术的概率为
故选：D．
9．D
【分析】本题主要考查了因式分解的应用，根据题意得出，因式分解得出，分类讨论得出或，，即可求解．
【详解】解：∵
∴，则
∵
∴
∴，
∴或
即或，故A，B不正确
∵
∴，故C选项不正确，D选项正确
故选：D．
10．C
【分析】本题考查了圆周角定理、相似三角形的判定与性质、勾股定理、全等三角形的判定与性质，，根据相似三角形的性质即可判断A，证明、、、四点共圆，得出，再证明，得出，从而即可判断B；设，则，，表示出，由此即可判断C；证明，求出，表示出，作于，于，由等面积法得出，结合勾股定理得出，证明，求出，再由的面积为计算即可得解，熟练掌握以上知识点并灵活运用，添加适当的辅助线是解此题的关键．
【详解】解：∵，，
∴，
∴，即，
∵，，
∴，
∵，
∴，
∴，
∴，
∴，
当时，，即，故A正确；
当时，，即，
∵，
∴，
∵，
∴，
∴、、、四点共圆，
∴，
∵，
∴，
∴，
∴四边形的周长为，故B正确；
设，则，，即，
∴，
∴当时，的面积最大为，故C错误；
∵，，
∴，
∴，即，
∴，
∵为的中点，
∴，
如图，作于，于，
∵，
∴，
∴，
∴，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴的面积为，故D正确；
故选：C．
11．2
【分析】根据的近似数即可得出结论．
【详解】解：，与最接近的整数是2
故答案为：2．
【点睛】此题考查的是求算术平方根的取值范围，掌握的近似数是解决此题的关键．
12．（答案不唯一）
【分析】本题考查了正比例函数的性质，根据正比例函数图象经过第二、四象限可得，由此即可得解，熟练掌握正比例函数的性质是解此题的关键．
【详解】解：写一个图象经过第二、四象限的正比例函数的表达式为：，
故答案为：（答案不唯一）．
13．
【分析】将原式通分，相加后再约分即可得出结果．
【详解】解：
，
故答案为：．
【点睛】本题考查了异分母分式的相加减，熟练运用通分、约分法则是解本题的关键．
14．
【分析】本题考查了解直角三角形的应用，正确理解题意是解题的关键．设，根据三角函数的定义，在和中，分别求出的值，再根据列方程，求出的值，即可进一步求得答案．
【详解】解：由题意得：，
设，则，
在中，，
∴，
在中，，
∴，
，
，
解得：，
，
，
∴图书馆的高度为．
故答案为：．
15．/
【分析】本题考查全等三角形的判定和性质，等腰三角形的判定和性质，勾股定理，连接，，在上取一点O，使，连接，，证明，得到，证明，得到，，证明，得到，再在中，根据勾股定理，求出，根据即可解决问题．
【详解】解：如图，连接，，在上取一点O，使，连接，，
∵A为的中点，为等腰直角三角形，，
∴，
∴，
又∵为等腰直角三角形，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
又∵，
∴，
∴，
∵，，，
∴，
又∵，
∴，
∴，
在中，由勾股定理，得，
∴．
故答案为：．
16．①②④
【分析】本题考查二次函数符号判断，根据得到抛物线过，再结合已知条件画出大致的函数图象，然后根据函数图象分析计算即可．
【详解】解：∵，
∴过，
∵，过点，，
∴函数的大致图象如下两种情况：
由函数图象可得，故①正确；
由函数图象可得当时，，
∵，
∴，
∴，
故②正确；
方程有两个不相等的实数根（且），可以看成抛物线与交点横坐标为，
有函数图象可得：当时，；当时，；
故③错误；
∵抛物线过点，
∴，
∴，整理得，，
∴，
∵抛物线过点，，
∴抛物线对称轴为直线，
∵，
∴，即，
∵，
∴解得，
∴，
故④正确；
综上所述，正确的有①②④，
故答案为：①②④．
17．（1）；（2）
【分析】本题考查的是实数的运算，分式的混合运算，熟知分式混合运算的法则，正确化简各数是解题的关键．
（1）直接利用特殊角的三角函数值、负整数指数幂的性质、零指数幂、二次根式的性质分别化简，进而得出答案；
（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到最简结果．
【详解】（1）解：原式
；
（2）解：原式
．
18．1
【分析】本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集，然后确定整数解即可．
【详解】解：解①得：，
解②得：，
∴不等式组的解集为，
∴不等式组的整数解为1．
19．(1)
(2)
【分析】本题考查了三角形内角和定理、角平分线的定义以及对顶角，利用三角形内角和定理及角平分线的定义，求出的度数是解题的关键．
（1）在中，利用三角形内角和定理可求出的度数；
（2）结合角平分线的定义可得出的度数，在中，利用三角形内角和定理可求出的度数，结合对顶角相等可得出的度数，再在中利用三角形内角和定理可求出的度数．
【详解】（1）解：∵中，，，
∴
故答案为：．
（2）平分，
．
在中，，，
，
．
于，
，
．
20．(1)小明和小华制作的盒子能装下这种牙膏，小思制作的盒子不能装下这种牙膏，理由见解析
(2)小明的制作更合理，理由见解析
【分析】（）要把牙膏放入牙膏盒内，则牙膏盒底面对角线长应大于或等于，利用咕咕咕定理判断即可求解；
（）设牙膏盒的高度为，分别求出小明和小华制作的牙膏盒的表面积和体积，进行比较即可判断求解；
本题考查了勾股定理的应用，整式加减的应用，理解题意是解题的关键．
【详解】（1）解：小明和小华制作的盒子能装下这种牙膏，小思制作的盒子不能装下这种牙膏，理由如下：
要把牙膏放入牙膏盒内，则牙膏盒底面对角线长应大于或等于，
∵，，，
∴小明和小华制作的盒子能装下这种牙膏，小思制作的盒子不能装下这种牙膏；
（2）解：小明的制作更合理，理由如下：
设牙膏盒的高度为，
则小明制作的牙膏盒表面积为：，
小华制作的牙膏盒表面积为：，
∵，
∴小明制作的牙膏盒材料更少，
又∵小明制作的牙膏盒体积为：，
小华制作的牙膏盒体积为：，
∴小明制作的牙膏盒体积更小，更方便取放牙膏，
综上，从节约材料又方便取放牙膏的角度来看，小明的制作更合理．
21．（1）43﹣12；（2）﹣1．
【详解】试题分析：根据二次根式的性质，分别表示出m、n的值，然后代入求值即可.
试题解析：∵m是的小数部分，n是的整数部分，
∴m=﹣2，n=4；
（1）（m﹣n）2=（﹣2﹣4）2=（﹣6）2=7﹣12+36=43﹣12；
（2）+m=+﹣2=﹣1．
22．(1)且
(2)
(3)
【分析】（1）根据题意，计算一元二次方程根的判别式大于或等于0，根据一元二次方程的定义得出，即可求解；
（2）根据恰好是等腰的腰长，令，解一元二次方程求得，进而即可求解；
（3）由(2)知：的三边长为，代入公式求得面积，进而根据角平分线的性质求得，再根据三角形面积公式即可求解．
【详解】（1）解：由题意得：，且，
化简得：，
解得：且；
（2）由题意知：恰好是等腰的腰长，
∴，
∵是关于的一元二次方程的两实数根，
∴，
解得，
∴，
解得，
∵，
∴的周长为：；
（3）由(2)知：的三边长为，
∴5，
∴，
过分别作，，，垂足分别为，
∵是△ABC角平分线的交点，
∴，
∴
，
解得，
∴．
【点睛】本题考查了一元二次方程的定义，一元二次方程根的判别式，等腰三角形的性质，角平分线的性质，综合运用以上知识是解题的关键．
23．(1)见解析；
(2)．
【分析】本题考查了垂径定理，勾股定理，切线的性质和判定，平行线的性质和判定，等腰三角形的性质和判定的应用，主要考查学生综合运用性质进行推理和计算的能力，正确作出辅助线是解题的关键．
（1）连，证明，可得，证明，可得，则，结论得证；
（2）延长交于点，由（1）知，求出，可求出，设半径为，则，解方程即可得解．
【详解】（1）证明：如图，连，
，
，
，
，
，
，
，
，
，
，
，
为的半径，
为的切线；
（2）解：如图，延长交于点，由（1）知，
，
，
，
，
，
在中，根据勾股定理得：，
设半径为，则，
，
．
的半径为．
24．（一）；（二）（1）；（2）
【分析】（一）如图1，由题意知，，，，则，，，，，根据，计算求解即可；
（二）（1）如图2，过作轴于，由题意知，，，，，，在中，由勾股定理求，证明，则，求得，，同理，则，求得，，则，，代入反比例函数解析式求，进而可得反比例函数解析式；
（2）如图3，取中点，作，取圆心，连接，，则，由正方形的性质，设，，在和中，由勾股定理得 ，，即，求的值，的值，进而可得的半径，然后代入圆的面积公式进行求解即可．
【详解】（一）解：如图1，
由题意知，，，，
∴，
∴，，
∴，，
∴，
∴此直角三角形的面积为；
（二）（1）解：如图2，过作轴于，
由题意知，，，，，，
在中，由勾股定理得，
∵，
∴，
∴，
∴，即，解得，，
同理，
∴，即，解得，，
∴，
∴，
∴，
∴反比例函数解析式为；
（2）解：如图3，取中点，作，取圆心，连接，，则，
由正方形的性质，
设，，
在中，由勾股定理得 ，
在中，由勾股定理得，
∴，解得，
∴，
∴的半径为，
∴，
∴圆的面积为．
【点睛】本题主要考查了正弦、正切，相似三角形的判断与性质，反比例函数，正方形的性质，圆的面积，勾股定理等知识．解题的关键在于对知识的熟练掌握与灵活运用．
25．(1)①√；②×；③×
(2)该一次函数的解析式为，“星联距离”为4
(3)或
【分析】（1）根据“星联函数”的定定义，逐个判定即可；
（2）分两种情形：情形一，当时，随的增大而增大；情形二，当时，随的增大而减小．分别求解即可．
（3）分两种情形：情形一，若，则；情形二，若时，则，．分别求解即可．
【详解】（1）解：①∵
∴
当时，
∴
∴
故①√；
②∵
∴
当时，
∴
∴
故②×；
③∵
当时，
∴
故③×．
（2）解：情形一，当时，随的增大而增大．
当，一次函数是“星联函数”，
，；，，
可得方程解得
该一次函数的解析式为，“星联距离”为．
情形二，当时，随的增大而减小．
当，一次函数是“星联函数”，
，；，，
可得方程解得
又，情形二不存在．
综上，该一次函数的解析式为，“星联距离”为4．
（3）解：“星联函数”解析式为的对称轴为．
情形一，若，则，由“星联函数”定义得
、是方程的两根，
由一元二次方程根与系数的关系，得，此种情形不存在．
情形二，若时，则，，
当时，．
①若，，
，，
此时星联距离为．
②若，则，不合题意，合去．
情形三，若，则由“星联函数”定义得
①-②，得，
方程①可以化为，
方程②可以化为，
、是方程的两根，由一元二次方程根与系数的关系得，，
符合题意．该函数的“星联距离”为：
．
综上，该函数的“星联距离”为或．
【点睛】本题考查新定义，一次函数图象性质，二次函数图象性质，理解新定义，熟练掌握一次函数与二次函数图象性质是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑