资源简介

中小学教育资源及组卷应用平台
北师大版六年级下册数学期末专题训练：计算题
学校:___________姓名：___________班级：___________考号：___________
一、计算题
1．应用比例内项的积与外项的积的关系，判断下面每组中的两个比是否可以组成比例。
7∶5和42∶30 12∶20和∶
2．求表面积。
3．求下面图形的表面积。
4．解方程或比例。
x＋x＝5 x∶32＝0.4∶6.4
5．口算．（括号里填除0以外的整数）
①28×12=( )
②2656÷8=( )
③45×8=( )
④870﹣500=( )
⑤275+100=( )
6．下面哪组中的两个比可以组成比例？把组成的比例写出来。
（1）5∶8和10∶16
（2）∶和12∶15
（3）0.6∶2.4和4∶15
（4）∶和∶
7．看图列出方程，并求出方程的解。
8．求圆锥的体积。（单位：）
9．如果＝，那么a＝( )。
10．计算图形的表面积。（单位：cm）
11．下面哪组中的四个数可以组成比例？把组成的比例写出来。
（1）6，8，15和24
（2）0.7，8，1.6和3.5
12．计算下面圆锥的体积。
13．看图列出方程，并求出方程的解。
14．解方程。
x∶＝12∶ 0.8x＋1.2x＝25
15．求下面图形的表面积与体积。
16．求体积。
17．解比例。
x∶30＝15∶45
0.4∶0.02＝20∶x
18．计算题。
∶＝x∶ ∶＝∶x
10∶50＝x∶40 x∶10＝∶
19．解方程。
12－5x＝6.5 22.5∶4＝x∶5
20．计算下面图形的体积。
21．计算。



22．a与b成反比例关系。
（1）a=2 b= a=4 b=16
（2）a=4 b=8 a=8 b=
（3）a= b=20 a=15 b=5
23．计算下左图中图形的体积与下右图中图形的表面积。
24．底面面积是28.26平方米，高是5米，求圆柱体的表面积．
25．列式计算。
已知圆柱的底面直径是4分米，高是直径的5倍，求它的侧面积。
26．我会计算圆锥的体积。
27．左右两个平行四边形形状一样，大小不同，求未知数X。
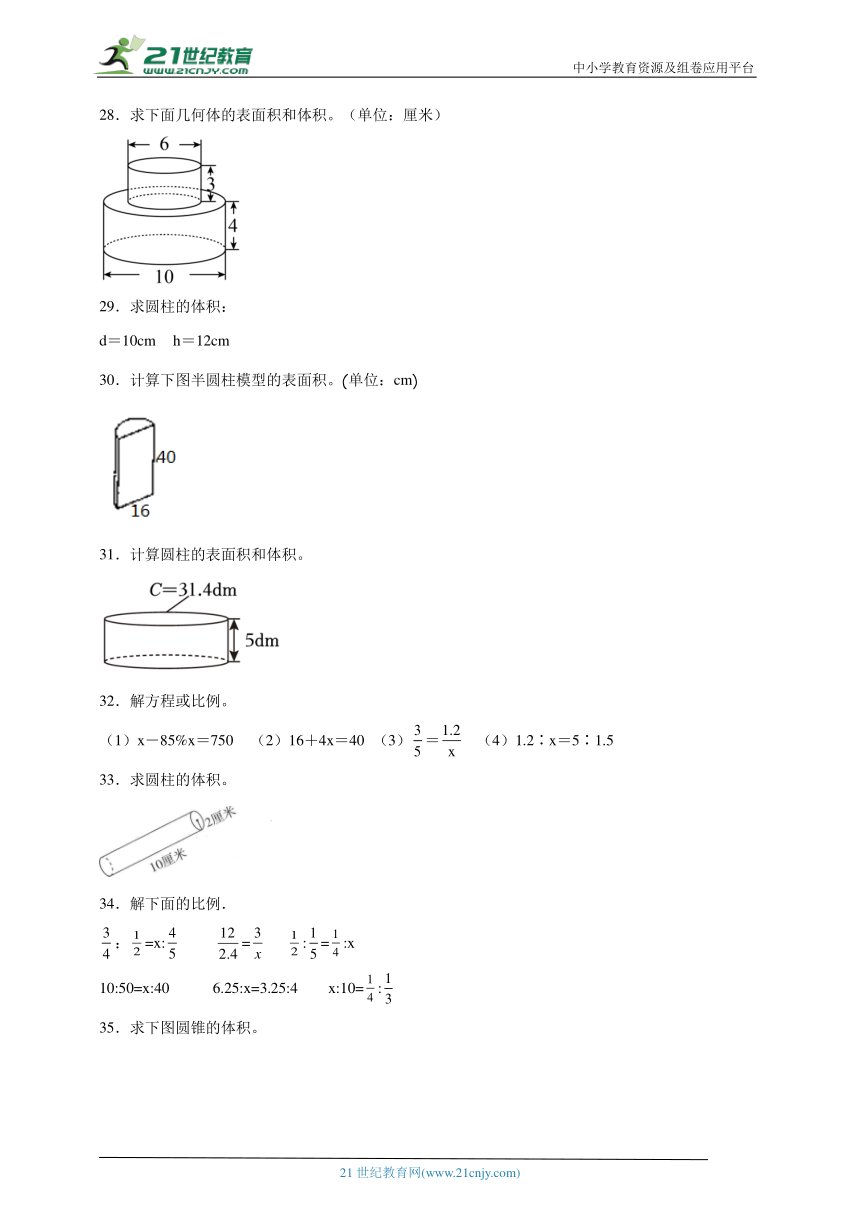
28．求下面几何体的表面积和体积。（单位：厘米）
29．求圆柱的体积：
d＝10cm h＝12cm
30．计算下图半圆柱模型的表面积。(单位：cm)
31．计算圆柱的表面积和体积。
32．解方程或比例。
（1）x－85%x＝750 （2）16＋4x＝40 （3）＝ （4）1.2∶x＝5∶1.5
33．求圆柱的体积。
34．解下面的比例．
：=x: = :=:x
10:50=x:40 6.25:x=3.25:4 x:10=:
35．求下图圆锥的体积。
36．计算下面图形的体积．
37．求圆柱的表面积：h＝4dm，r＝2dm
38．用简便方法计算．
999.9×999.9+99.99
《北师大版六年级下册数学期末专题训练：计算题》参考答案
1．7∶5和42∶30可以组成比例；12∶20和不能组成比例
【分析】根据比例的基本性质：在比例中，两个外项的积等于两个内项的积。据此判断能否组成比例。
【详解】（1）因为7×30＝210，5×42＝210，两外项的积与两内项的积相等，所以7∶5和42∶30可以组成比例；
（2）因为12×＝3，20×＝4，两外项的积与两内项的积不相等，所以不能组成比例。
2．722.2m2
【分析】根据圆柱的表面积公式：表面积＝底面积×2＋侧面积，代入数据，即可解答。
【详解】3.14×（10÷2）2×2＋3.14×10×18
＝3.14×52×2＋31.4×18
＝3.14×25×2＋565.2
＝78.5×2＋565.2
＝157＋565.2
＝722.2（m2）
3．244.92cm2
【分析】根据圆柱的表面积公式：表面积＝底面积×2＋侧面积，侧面积＝底面周长×高，代入数据，即可解答。
【详解】3.14×（6÷2）2×2＋3.14×6×10
＝3.14×32×2＋18.84×10
＝3.14×9×2＋188.4
＝28.26×2＋188.4
＝56.52＋188.4
＝244.92（cm2）
圆柱的表面积是244.92cm2。
4．x＝；x＝2
【分析】（1）先化简，再根据等式的性质解答即可；
（2）先根据比例的基本性质：两内项之积等于两外项之积，变为一般的方程，然后再根据等式的性质解答即可。
【详解】（1）x＋x＝5
解：x＝5
x÷＝5÷
x＝
（2）x∶32＝0.4∶6.4
解：6.4x＝32×0.4
6.4x＝12.8
6.4x÷6.4＝12.8÷6.4
x＝2
5． 336 332 360 370 375
【详解】①28×12=336 ②2656÷8=332 ③45×8=360 ④870﹣500=370 ⑤275+100=375
故答案为336，332，360，370,375
6．（1）能组成比例，比例为：5∶8＝10∶16；
（2）能组成比例，比例为：∶＝12∶15；
（4）能组成比例，比例为：∶2＝∶。
【分析】分别计算所给比的比值，根据比例的意义：两个比值相等的比组成比例，据此判断即可。
【详解】（1）5∶8
＝5÷8
＝
10∶16
＝10÷16
＝
＝
两个比的比值相等，所以能组成比例，比例为：5∶8＝10∶16
（2）∶
＝÷
＝×4
＝
12∶15
＝12÷15
＝
＝
两个比的比值相等，所以能组成比例，比例为：∶＝12∶15
（3）0.6∶2.4
＝0.6÷2.4
＝0.25
＝
4∶15
＝4÷15
＝
≠，两个比不能组成比例。
（4）∶
＝÷
＝×2
＝
∶
＝÷
＝×
＝
两个比的比值相等，能组成比例，比例为：∶2＝∶
7．＝5
【分析】从图中可知，天平左边有3个g重的物品，右边有1个g重的物品和1个10g重的物品，此时天平平衡，即天平左、右两边物品的质量相等，据此列出方程，并求解。
【详解】3＝＋10
解：3－＝＋10－
2＝10
2÷2＝10÷2
＝5
8．84.78cm3
【分析】根据圆锥的体积公式：体积＝底面积×高×，代入数据，即可解答。
【详解】3.14×（6÷2）2×9×
＝3.14×9×9×
＝28.26×9×
＝254.34×
＝84.78（cm3）
9．9
【详解】略
10．261.6cm2
【分析】观察图形可知，这个图形的表面积是圆柱的侧面积：S＝底面周长×高和长方体的表面积：S＝（ab＋ah＋bh）×2之和；据此计算即可解答。
【详解】（10×2＋10×4＋2×4）×2＋3.14×4×10
＝（20＋40＋8）×2＋3.14×4×10
＝（60＋8）×2＋12.56×10
＝68×2＋125.6
＝136＋125.6
＝261.6（cm2）
11．（1）不可以
（2）可以；0.7∶1.6＝3.5∶8
【分析】判断下面每组中四个数能否组成比例，可根据比例的基本性质：在比例中，两个外项的积等于两个内项的积，来判断即可。
【详解】由分析可知：
（1）因为6×24＝144，8×15＝120，即6×24≠8×15，除此之外，其他组合的乘积也不相等，所以6，8，15和24不可以组成比例。
（2）因为0.7×8＝5.6，1.6×3.5＝5.6，即0.7×8＝1.6×3.5，所以0.7，8，1.6和3.5可以组成比例，可以组成：0.7∶1.6＝3.5∶8。（答案不唯一）
12．这个圆锥的体积是18.84立方厘米。
【分析】
已知圆锥的底面直径和高，利用圆锥的体积V＝ πr2h ， 即可求出这个圆锥的体积。
【详解】
×3.14×（4÷2）2×4.5
＝3.14×4×1.5
＝18.84 （立方厘米）
答：这个圆锥的体积是18.84立方厘米。
13．0.6km
【分析】已知奇思平均每天跑skm，一周7天共晨跑4.2km，等量关系：平均每天跑的路程×7＝一周晨跑的路程，据此列出方程，并求解。
【详解】7s＝4.2
解：7s÷7＝4.2÷7
s＝0.6
奇思平均每天跑0.6km。
14．x＝72；x＝12.5
【分析】（1）首先根据比例的基本性质化简，然后根据等式的性质，两边同时乘8即可。
（2）首先化简，然后根据等式的性质，两边同时除以2即可。
【详解】（1）x∶＝12∶
解：x＝×12
x＝9
x×8＝9×8
x＝72
（2）0.8x＋1.2x＝25
解：2x＝25
2x÷2＝25÷2
x＝12.5
15．1884dm2，6280dm3
【分析】根据圆柱的表面积＝底面圆周长×高＋2个底面圆面积，底面周长为C＝πd，代入即可计算；根据圆柱的体积公式V＝Sh，已知图形的直径为20dm，高为20dm，计算出半径：（直径÷2），然后把数据分别代入公式解答。
【详解】3.14×20×20＋3.14×（20÷2）2×2
＝1256＋3.14×102×2
＝1256＋3.14×100×2
＝1256＋628
＝1884（dm2）
3.14×（20÷2）2×20
＝3.14×102×20
＝3.14×100×20
＝314×20
＝6280（dm3）
这个圆柱的表面积是1884 dm2，体积是6280dm3。
16．188.4cm3
【分析】组合体体积＝底面直径是6cm，高是4cm的圆柱的体积＋底面直径是6cm，高是（12－4）cm的圆锥的体积，根据圆柱的体积公式：V＝πr2h，圆锥的体积公式：V＝πr2h，代入数据，即可解答。
【详解】3.14×（6÷2）2×4＋3.14×（6÷2）2×（12－4）×
＝3.14×32×4＋3.14×32×8×
＝3.14×9×4＋3.14×9×8×
＝28.26×4＋28.26×8×
＝113.04＋226.08×
＝113.04＋75.36
＝188.4（cm3）
组合体的体积是188.4cm3。
17．x＝10；
x＝1；x＝58
【分析】x∶30＝15∶45，根据比例的基本性质，先写成45x＝30×15的形式，根据等式的性质2，两边同时÷45即可；
，根据比例的基本性质，先写成的形式，根据等式的性质2，两边同时÷即可；
0.4∶0.02＝20∶x，根据比例的基本性质，先写成0.4x＝0.02×20的形式，根据等式的性质2，两边同时÷0.4即可；
，根据比例的基本性质，先写成15x＝29×30的形式，根据等式的性质2，两边同时÷15即可。
【详解】x∶30＝15∶45
解：45x＝30×15
45x＝450
45x÷45＝450÷45
x＝10
解：
0.4∶0.02＝20∶x
解：0.4x＝0.02×20
0.4x＝0.4
0.4x÷0.4＝0.4÷0.4
x＝1
解：15x＝29×30
15x＝870
15x÷15＝870÷15
x＝58
18．x＝；x＝
x＝8；x＝
【分析】根据比例的基本性质，即内项之积等于外项之积，转化为常见的方程模式，再根据方程的基本性质进行方程的解答。
【详解】∶＝x∶
解：
x＝
x＝
∶＝∶x
解：
x＝
x＝
10∶50＝x∶40
解：50x＝10×40
50x＝400
50x÷50＝400÷50
x＝8
x∶10＝∶
解：x＝×10
x＝
19．x＝1.1；x＝28.125；x＝3
【分析】（1）方程左右两边同时加上5x，再交换方程左右两边的式子，方程左右两边同时减去6.5，最后方程左右两边同时除以5，求出方程的解；
（2）利用比例的基本性质，把比例方程转化为普通方程，方程左右两边同时除以4，求出方程的解；
（3）利用比与除法的关系，把比转化为除法，方程左右两边同时乘x，再交换方程左右两边的式子，最后方程左右两边同时除以，求出方程的解。
【详解】
解：
解：
解：
20．183.69cm3；100.48cm3；260cm3；64cm3
【分析】（1）根据圆柱的体积公式V＝πr2h，代入数据计算，求出圆柱的体积；
（2）根据圆锥的体积公式V＝πr2h，代入数据计算，求出圆锥的体积；
（3）根据长方体的体积公式V＝abh，代入数据计算，求出长方体的体积；
（4）根据正方体的体积公式V＝a3，代入数据计算，求出正方体的体积。
【详解】（1）3.14×32×6.5
＝3.14×9×6.5
＝183.69（cm3）
圆柱的体积是183.69cm3。
（2）×3.14×（8÷2）2×6
＝×3.14×42×6
＝×3.14×16×6
＝100.48（cm3）
圆锥的体积是100.48cm3。
（3）8×5×6.5
＝40×6.5
＝260（cm3）
长方体的体积是260cm3。
（4）4×4×4
＝16×4
＝64（cm3）
正方体的体积是64cm3。
21．132；1185；15
4900；36000；100
27；90500；132.6
【分析】46＋32＋54，根据加法交换律，原式化为：46＋54＋32，再进行计算。
546＋785－146，根据带符号搬家，原式化为：546－146＋785，再进行计算。
0.7＋3.9＋4.3＋6.1，根据加法交换律，原式化为：0.7＋4.3＋3.9＋6.1，再根据加法结合律，原式化为：（0.7＋4.3）＋（3.9＋6.1），再进行计算。
25×49×4，根据乘法交换律，原式化为：25×4×49，再进行计算。
8×（36×125），去掉括号，原式化为：8×36×125，再根据乘法交换律，原式化为：8×125×36，再进行计算。
8×4×12.5×0.25，根据乘法交换律，原式化为：8×12.5×4×0.25，再根据乘法结合律，原式化为：（8×12.5）×（4×0.25），再进行计算。
2.7×4.8＋2.7×5.2，根据乘法分配律的逆运算，原式化为：2.7×（4.8＋5.2），再进行计算。
905×99＋905，根据乘法分配律的逆运算，原式化为：905×（99＋1），再进行计算。
13×（10＋0.2），根据乘法分配律，原式化为：13×10＋13×0.2，再进行计算。
【详解】46＋32＋54
＝46＋54＋32
＝100＋32
＝132
546＋785－146
＝546－146＋785
＝400＋785
＝1185
0.7＋3.9＋4.3＋6.1
＝0.7＋4.3＋3.9＋6.1
＝（0.7＋4.3）＋（3.9＋6.1）
＝5＋10
＝15
25×49×4
＝25×4×49
＝100×49
＝4900
8×（36×125）
＝8×36×125
＝8×125×36
＝1000×36
＝36000
8×4×12.5×0.25
＝8×12.5×4×0.25
＝（8×12.5）×（4×0.25）
＝100×1
＝100
2.7×4.8＋2.7×5.2
＝2.7×（4.8＋5.2）
＝2.7×10
＝27
905×99＋905
＝905×（99＋1）
＝905×100
＝90500
13×（10＋0.2）
＝13×10＋13×0.2
＝130＋2.6
＝132.6
22．（1）32；（2）4；（3）
【分析】两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的乘积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。据此解答即可。
【详解】（1）a×b的积：4×16＝64，当a＝2，b的值为：64÷2＝32，即b＝32；
（2）a×b的积：4×8＝32，当a＝8，b的值为：32÷8＝4，即b＝4；
（3）a×b的积：15×5＝75，当b＝20，b的值为：75÷20＝，即b＝；
23．753.6立方厘米；1381.6平方厘米
【分析】根据作图可知，是由一个圆柱和一个圆锥组成，根据圆柱的体积公式：底面积×高，圆锥的体积同时：底面积×高÷3，把数代入即可求解；
第二个图的表面积：相当于下面一个圆柱的表面积加上上面圆柱的侧面积，根据圆柱的侧面积公式：底面周长×高，圆柱的底面面积：S＝πr2，把数代入公式，把两个圆柱的侧面积相加，再加两个下面圆柱的底面积即可求解。
【详解】第一个：
3.14×（6÷2）2×20＋3.14×（12÷2）2×5÷3
＝3.14×9×20＋3.14×36×5÷3
＝565.2＋188.4
＝753.6（立方厘米）
第二个：
3.14×（20÷2）2×2＋3.14×20×8＋3.14×8×10
＝3.14×100×2＋3.14×160＋3.14×80
＝628＋502.4＋251.2
＝1381.6（平方厘米）
24．150.72平方米
【详解】半径：r2=18.84÷3.14=9 r=3
侧面积：2×3.14×3×5= 94.2（平方米）
表面积：94.2+28.26×2=150.72（平方米）
25．251.2平方分米
【分析】根据“高是直径的5倍”用4×5求出高，然后根据侧面积公式：即可解答。
【详解】4×3.14×4×5
＝12.56×4×5
＝251.2（平方分米）
答：它的侧面积是251.2平方分米。
【点睛】此题主要考查学生对侧面积公式的理解与实际应用解题能力，需要牢记公式：。
26．75.36立方厘米
【分析】根据圆锥体体积公式，即圆锥的体积＝×[（d÷2）πh]，可解答此题。
【详解】×[（6÷2）×3.14×8）]
＝×（9×3.14×8）
＝×226.08
＝75.36（立方厘米）
【点睛】本题要求对圆锥的体积公式能熟练的应用，认真计算。
27．16
【解析】略
28．339.12平方厘米；398.78立方厘米
【分析】虽然上面的圆柱挡住了下面大的圆柱的底面的一部分，但是通过平移可以将上面的圆柱的底面平移到下面圆柱的底面，最后立体图形的表面积＝大圆柱的表面积＋小圆柱的侧面积。圆柱的侧面积：S＝Ch＝πdh，圆柱的表面积：S＝2πr2＋πdh。立体图形的体积等于两个圆柱体积之和，圆柱的体积：V＝Sh＝πr2h。据此解答。
【详解】（10÷2）2×3.14×2＋10×3.14×4＋6×3.14×3
＝52×3.14×2＋125.6＋56.52
＝25×2×3.14＋125.6＋56.52
＝157＋125.6＋56.52
＝339.12（平方厘米）
这个几何体的表面积是339.12平方厘米。
（6÷2）2×3.14×3＋（10÷2）2×3.14×4
＝32×3.14×3＋52×3.14×4
＝9×3.14×3＋25×3.14×4
＝84.78＋314
＝398.78（立方厘米）
这个几何体的体积是398.78立方厘米。
29．942cm3
【分析】根据圆柱的体积公式：V＝πr2h作答。
【详解】3.14×（10÷2）2×12
＝（3.14×3）×（25×4）
＝9.42×100
＝942（cm3）
【点睛】在计算此题时，要仔细观察算式的特点，灵活运用乘法交换律和乘法结合律可以使计算简便
30．1845.76cm2
【分析】通过观察模型，这个模型的表面积分为四个面，一个弧形侧面加一个长方形侧面积加两个半圆形底面积，相当于一个整圆面积，其中需要用到的面积公式有：、和长方形面积＝长×宽，以此解答。
【详解】底面半径：16÷2＝8（cm）
底圆面积：8×3.14＝200.96（cm2）
弧形侧面积：16×3.14×40÷2
＝2009.6÷2
＝1004.8（cm2）
长方形面积：40×16＝640（cm2）
表面积：1004.8＋200.96＋640
＝1205.76＋640
＝1845.76（cm2）
【点睛】本题考查了学生对圆柱体表面积的理解和灵活应用，需要把物体分面来解答。
31．549.5dm2；392.5dm3
【分析】已知圆柱的底面周长C＝31.4dm，根据圆的周长公式C＝2πr可知，r＝C÷π÷2，由此先求出圆柱的底面半径；然后根据圆柱的表面积S表＝S侧＋2S底，其中S侧＝Ch，S底＝πr2，圆柱的体积V＝πr2h，代入数据计算即可。
【详解】31.4÷3.14÷2
＝10÷2
＝5（dm）
31.4×5＋3.14×52×5
＝157＋3.14×25×5
＝157＋78.5×5
＝157＋392.5
＝549.5（dm2）
3.14×52×5
＝3.14×25×5
＝78.5×5
＝392.5（dm3）
圆柱的表面积是549.5dm2，体积是392.5dm3。
32．（1）x＝5000；（2）x＝6；（3）x＝2；（4）x＝0.36
【分析】（1）先把85%化成0.85，再把方程左边化简为0.15x，最后根据等式的基本性质给方程两边同时除以0.15即可；
（2）先给方程两边同时减去16，再同时除以4即可；
（3）先根据比例的基本性质把方程化成3x＝1.2×5，再给方程两边同时除以3即可；
（3）先根据比例的基本性质把方程化成5x＝1.2×1.5，再给方程两边同时除以5即可。
【详解】（1）x－85%x＝750
解：x－0.85x＝750
0.15x＝750
x＝750÷0.15
x＝5000
（2）16＋4x＝40
解：4x＝24
x＝24÷4
x＝6
（3）＝
解；3x＝1.2×5
3x＝6
x＝6÷3
x＝2
（4）1.2∶x＝5∶1.5
解：5x＝1.2×1.5
5x＝1.8
x＝1.8÷5
x＝0.36
33．125.6立方厘米
【分析】在已知圆柱的底面半径和高，求体积可通过V圆柱＝πr2h代入数据直接计算即可。
【详解】3.14×2×2×10
＝3.14×4×10
＝125.6（立方厘米）
【点睛】求体积的条件都是已知的，直接运用公式计算即可，注意牢记公式和计算的准确性。
34．x=；x=0.6 ； x=
x=8； x=20 ； x=
【详解】：=x: = :=:x
解： x=× 解：12x=2.4×3 解：x=×
x= x=0.6 x=
10:50=x:40 6.25:x=1.25:4 x:10=:
解： 50x=10×40 解： 3.25x=6.25×4 解： x=×10
x=8 x=20 x=
35．527.52 cm3
【分析】圆锥的体积＝底面积×高×，由此根据公式结合图中数据计算即可。
【详解】3.14×（12÷2）2×14×
＝3.14×36×14×
＝113.04×14×
＝1582.56×
＝527.52（cm3）
36．471立方厘米
【详解】圆锥的体积=底面积×高×，由此根据圆锥的体积公式计算体积即可.
×3.14×52×18=471（cm3）
答：图形的体积是471立方厘米.
37．75.36dm2
【分析】圆柱体表面积＝圆柱侧面积＋两个底面积，已知圆柱底面半径，通过公式：，可求出底面积，通过侧面积公式：，即可解答。
【详解】侧面积：2×2×3.14×4
＝4×3.14×4
＝50.24（dm2）
底面积：2×3.14＝12.56（dm2）
表面积：50.24＋12.56×2
＝50.24＋25.12
＝75.36（dm2）
【点睛】此题考查了学生对圆柱体的表面积的理解与应用，需要牢记公式。
38．999900
【详解】999.9×999.9+99.99
=999.9×999.9+999.9×0.1
=999.9×(999.9+0.1)
=999.9×1000
=999900
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)

展开更多......

收起↑