资源简介

2025年四川省遂宁市射洪市射洪中学校中考二模数学试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．的相反数是（ ）
A． B． C． D．
2．据统计，2024年我国外贸首次突破43万亿元大关，同比增长5％，连续第8年保持货物贸易第一大国地位．将数据“43万亿”用科学记数法表示为（ ）．
A． B． C． D．
3．如图所示几何体的左视图是（　　）
A． B．
C． D．
4．下列运算正确的是（ ）
A． B． C． D．
5．不等式组的解集在数轴上表示为（　　）
A． B．
C． D．
6．将一组数，按以下方式进行排列：
则第八行左起第1个数是（ ）
A． B． C． D．
7．若关于x的方程有解，则a的值不可能是（ ）
A．0 B．2 C．4 D．6
8．如图，，，相交于O，，，则线段的长为（　　）
A．6 B．10 C．8 D．7
9．如图，的直径，以点A为圆心为半径画，与交于点C，D，以点B为圆心为半径画，与交于点E，F，则图中阴影部分的面积为（ ）．
A． B． C． D．
10．抛物线的图象如图所示，对称轴为直线．下列说法：①；②；③（t为全体实数）；④若图象上存在点和点，当时，满足，则m的取值范围为．其中正确的个数有（ ）

A．1个 B．2个 C．3个 D．4个
11．在开展“慈善一日捐”活动中，某单位名员工捐款情况如下表：
捐款（元） 50 100 150 200 300
员工数（人） 11 19 6 3 1
则此次捐款数额的中位数是 元．
二、填空题
12．把多项式分解因式的结果是 ．
13．如图，，是的切线，A，B是切点，点C是上一点，若，则 ．
14．“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，弦，垂足为点D，寸，尺(10寸)，则圆的直径长度是 ．
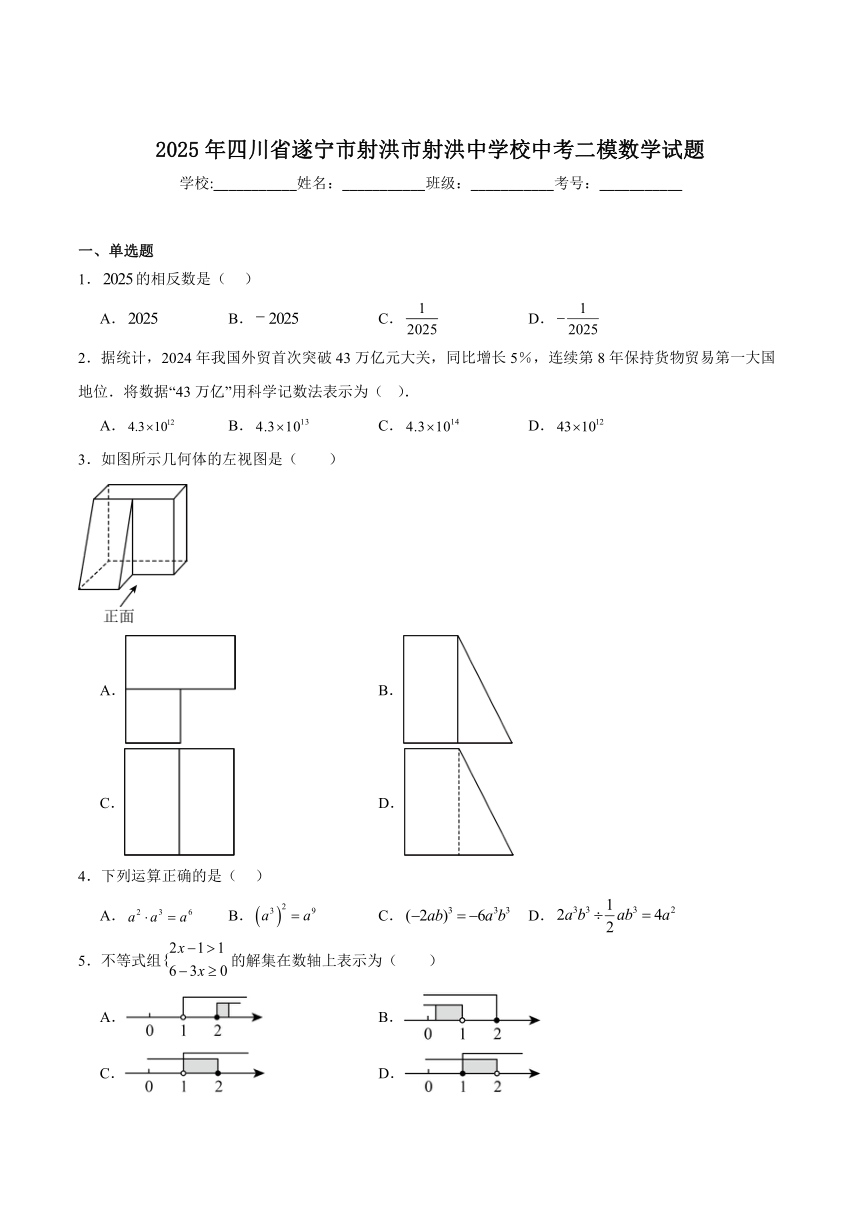
15．如图，以的边、为腰分别向外作等腰直角、，连结、、，过点的直线分别交线段、于点、，以下说法：①当时，；②；③若，，，则；④当直线时，点为线段的中点．正确的有 ．(填序号)

三、解答题
16．计算：．
17．先化简，再求值.
，其中
18．为贯彻落实党的二十大关于深化全民阅读活动的重要部署，教育部印发了《全国青少年学生读书行动实施方案》，于是某中学开展了以“书香润校园，好书伴成长”为主题的系列读书活动．学校为了解学生周末的阅读情况，采用随机抽样的方式获取了若干名学生的周末阅读时间数据，整理后得到下列不完整的图表：
类别 A类 B类 C类 D类
阅读时长t（小时）
频数 8 m n 4

请根据图表中提供的信息，解答下面的问题：
(1)此次调查共抽取了_________名学生， _________， _________；
(2)扇形统计图中，B类所对应的扇形的圆心角是_________度；
(3)已知在D类的4名学生中有两名男生和两名女生，若从中随机抽取两人参加阅读分享活动，请用列表或画树状图的方法求出恰好抽到一名男生和一名女生的概率．
19．某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台，经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低1元，就可多售出5台，若供货商规定这种空气净化器售价不低于330元/台，代理销售商每月要完成不低于450台的销售任务．
(1)试确定月销售量与售价之间的函数关系式，并求出售价的范围；
(2)当售价定为多少时，商场每月销售这种空气净化器所获的利润最大，最大利润是多少？
20．如图，反比例函数的图象与一次函数的图象交于点，．
(1)求反比例函数的表达式；
(2)直接写出关于的不等式的解集：___________；
(3)连接，，求的面积．
21．如图，活动课上，小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度，她先在山脚下的点E处测得山顶A的仰角是30°，然后，她沿着坡度i=1：1的斜坡按速度20米/分步行15分钟到达C处，此时，测得点A的俯角是15°．图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上，求出建筑地所在山坡AE的高度AB．（精确到0.1米，参考数据：≈1.41）．
22．在平行四边形中，对角线相交于点O，E，F分别是的中点，连接．
(1)如图1，求证：四边形是平行四边形；
(2)如图2，当线段与线段满足什么数量关系时，四边形是矩形？请说明理由；
(3)若四边形是矩形，，求的长．
23．阅读理解题．
定义：如果四边形的某条对角线平分一组对角，那么把这条对角线叫做“和谐线”，该四边形叫做“和谐四边形”．
如图，在四边形ABDC中，对角线BC平分∠ACD和∠ABD，那么对角线BC叫“和谐线”，四边形ABDC就称为“和谐四边形”．
问题：
(1)下列四边形：
①平行四边形、②矩形、③菱形、④正方形，
其中是“和谐四边形”的有______；（填序号）
(2)四边形ABCD是“和谐四边形”，，，，求四边形ABCD“和谐线”的长．（画出图形并写出解答过程）
24．如图，为的切线，为切点，直线交于点，，过点作的垂线，垂足为点，交于点，延长与交于点，连接，．
(1)求证：直线为的切线；
(2)求证：；
(3)若，，求的长．
25．如图，已知抛物线与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为．
（1）求抛物线的解析式；
（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ．当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由．
（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且．在y轴上是否存在点F，使得为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．
《2025年四川省遂宁市射洪市射洪中学校中考二模数学试题》参考答案
1．B
解：的相反数是，
故选：B．
2．B
解：将数据“43万亿”用科学记数法表示为，
故选：B．
3．D
解：从左边看，是一个矩形和一个直角三角形，它两中间有一条纵向的虚线．
故选：D．
4．D
解：A． ，此选项不正确，不符合题意；
B．，此选项不正确，不符合题意；
C． ，此选项不正确，不符合题意；
D．，此选项正确，符合题意；
故选：D．
5．C
解：，
∵解不等式得：x＞1，
解不等式得：，
∴不等式组的解集是：1＜x≤2，
在数轴上表示为：，
故选：C．
6．C
解：由图可知，第一行共有1个数，第二行共有2个数，第三行共有3个数，
归纳类推得：第七行共有个数，
则第八行左起第1个数是，
故选：C．
7．D
解：当时，则，方程有解，故A选项不符合题意；
当且，即，
解得：
∴且，∴a可以为2、4，不可能为6，
故B、C选项不符合题意，D选项符合题意；
故选：D．
8．A
解：∵，
∴，
∴，
∵，
∴，
∴，
又∵，，
∴，
解得，
∵，
∴，
故选：A．
9．D
解：由圆的对称性可知：左右两边的阴影部分的面积相同，
连接，作，由作图可知：，
∴均为等边三角形，
∴，弓形和弓形的面积相同，
∵，
∴；
故选D．
10．C
∵抛物线的开口向下，对称轴为直线，
∴，和的函数值相同，
由图可知，当时的函数值小于0，
∴，
∴，
故①正确；
由图象可知，，根据对称轴，得，
∴
∴，
故②正确；
∵抛物线的开口向下，对称轴为直线，
∴抛物线的最大值为，
当时，其函数值为，
∴，
∴，
∵，
∴，
∴，
故③错误；
如图所示，和点满足，

∴和点关于对称轴对称，
∴,
∵,
∴,
解得，
故④正确；
故选C．
11．
解：由表中数据可知，第名和第名员工捐款数额都为元，
此次捐款数额的中位数是（元），
故答案为：．
12．
解：，
故答案为： ．
13．55
解：，是的切线，A，B是切点，，如图，连接，，
∴，，
∴，
∴，
故答案为：55．
14．26
解：连接，
设的半径是寸，
∵弦，垂足为点，
寸，
寸，
寸，
，
，
，
∴直径的长度为寸．
故答案为：26．
15．①②④
解：①当时，是等边三角形，
∴
∴
∵等腰直角、，
∴，
∴，
∴；故①正确；
②∵等腰直角、，
∴，，
∴，
∴，
∴；故②正确；
④如图所示，作直线于点， 过点作于点，过点作于点，

∵，，
∴，
又，
∴，
又∵，
∴，
同理得，，
∴，，，
∵，，
∴，
∴，即是的中点，故④正确，
∴，
设，则，
在中，，
在中，，
∴，
∴，
解得：，
∴，
∴，
∴，
∴，
在中，，
∴,故③错误，
故答案为：①②④．
16．
解：
．
17．原式=
原式=
=6
=-
当
则原式=-=-1
18．(1)40，18，10
(2)162
(3)
（1）解：(名)，
，
，
故答案为：40，18，10；
（2）解：，
故答案为：162；
（3）解：画树状图为：

共有12种等可能的结果，其中一名男生和一名女生的结果数为8，
所以恰好抽到一名男生和一名女生的概率．
19．(1)（）
(2)当售价为330元/台时，月利润最大为71500元．
（1）由题意，得：.
∵售价不低于330元/台，
∴，
∵数量不低于450台，
∴，即，解得，，
∴．
答：y与x之间的函数关系式为：（）；
（2）由题意，得：，
∵，
∴在对称轴的右侧w随x的增大而减小，
∴时，w最大=71500．
答：当售价为330元/台时，月利润最大为71500元．
20．(1)
(2)或
(3)12
（1）∵点在一次函数的图象上，
∴，
解得，
∴点．
∵反比例函数经过点，
∴，
∴反比例函数关系式为；
（2）当或时．
故答案为：或；
（3）如图所示，当时，，所以点；
当时，，所以点．
∴，
∴．
21．建筑地所在山坡AE的高度AB约为105.8米．
解：作EF⊥AC于点F，
根据题意，CE=20×15=300米，
∵i=1：1，
∴tan∠CED=1，
∴∠CED=∠DCE=45°，
∵∠ECF=90°﹣45°﹣15°=30°，
∴EF=CE=150米，
∵∠CEF=60°，∠AEB=30°，
∴∠AEF=180°﹣45°﹣60°﹣30°=45°，
∴AF=EF=150米，
∴AE= （米），
∴AB=×150≈105.8（米）．
答：建筑地所在山坡AE的高度AB约为105.8米．
22．(1)见解析
(2)当时， 四边形是矩形，证明见解析
(3)
（1）证明：∵四边形是平行四边形，
∴，
∵E，F分别是的中点，
∴，
∴，
∴四边形是平行四边形；
（2）解：当时，四边形是矩形，证明如下：
∵四边形是平行四边形，
∴，
∵E，F分别是的中点，
∴，
∴，
∵，即，
∴
∵四边形是平行四边形；
∴四边形是矩形；
（3）解：∵四边形是矩形，
∴由（2）可知，
∵，
∴，
在中，由勾股定理得，
∴，
∴或（舍去），
∴，
∴，
∴由平行四边形的性质可得．
23．(1)③④
(2)或
（1）具有对角线平分一组对角性质的有菱形、正方形，
故答案为：③④；
（2）分两种情况：
①当AC是和谐线时，如图1，
∵AC平分∠BAD、∠BCD，在△ABC中，，，
∵，
∴，
∵．
②当BD是和谐线时，如图2，过D作DH⊥AB于H，
∵，
∴，
∴△BDH是等腰直角三角形，
∴，
设，则，，
∴，
∴，∴，
∴
综上所述：四边形ABCD的和谐线为或．
24．(1)见解析
(2)见解析
(3)10
（1）证明：如图，连接，
是的切线，
．
于D
．
又，
．
,
，
为的半径，
∴直线为的切线．
（2）证明：，
．
，
，
即．
又，
；
（3）解：，
．
设
．
在中，由勾股定理，得．
解得，（不合题意，舍去）．
．
是的直径，
．
25．（1）；（2）四边形OCPQ是平行四边形，理由见详解；（3）（0，）或（0，1）或（0，-1）
解：（1）∵抛物线与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线，
∴B（4，0），C（0，4），
设抛物线，把C（0，4）代入得：，解得：a=1，
∴抛物线的解析式为：；
（2）∵B（4，0），C（0，4），
∴直线BC的解析式为：y=-x+4，
设P（x，-x+4），则Q（x，），（0≤x≤4），
∴PQ=-x+4-()==，
∴当x=2时，线段PQ长度最大=4，
∴此时，PQ=CO，
又∵PQ∥CO，
∴四边形OCPQ是平行四边形；
（3）过点Q作QM⊥y轴，过点Q作QN∥y轴，过点E作EN∥x轴，交于点N，
由（2）得：Q（2，-2），
∵D是OC的中点，
∴D（0，2），
∵QN∥y轴，
∴，
又∵，
∴，
∴，
∴，即：，
设E（x，），则，解得：，（舍去），
∴E（5，4），
设F（0，y），则，
，，
①当BF=EF时，，解得：，
②当BF=BE时，，解得：或，
③当EF=BE时，，无解，
综上所述：点F的坐标为：（0，）或（0，1）或（0，-1）．
．

展开更多......

收起↑