资源简介

中小学教育资源及组卷应用平台
2024-2025学年第二学期七年级数学期末模拟卷（22）
（考试时间：120分钟 试卷满分：130分）
学校： 年级： 姓名： 考号：
一．选择题（共10小题，满分30分，每小题3分，每题均有四个选项，其中只有一个选项符合规定）
1．计算的结果是（ ）
A． B． C． D．
2．博物馆是历史的见证者和收录者，是人们直观感受历史脉络，提升历史认知的重要场所．以下四个博物馆标识，其文字上方的图案不是轴对称图形的是（ ）
A． B． C． D．
3．下列式子中，为最简二次根式的是（ ）
A． B． C． D．
4．下列命题为假命题的是（ ）
A．对顶角相等
B．有一条公共边，且互补的两个角互为邻补角
C．两直线平行，内错角相等
D．过直线外一点有且只有一条直线与已知直线平行
5．嫦娥六号于2024年6月2日成功着陆在月球背面南极一艾特肯盆地预选着陆区，开启人类探测器首次在月球背面实施的样品采集任务．嫦娥六号采用了机械臂表取和钻具钻取两种方式共采集样品，假设机械臂表取采集的样品数量比钻具钻取采集的样品数量的4倍还多．若设机械臂表取样品，钻具钻取样品，则根据题意可列方程组为（ ）
A． B．
C． D．
6．若代数式，，则的值（ ）
A．一定是负数 B．一定是正数
C．一定不是负数 D．一定不是正数
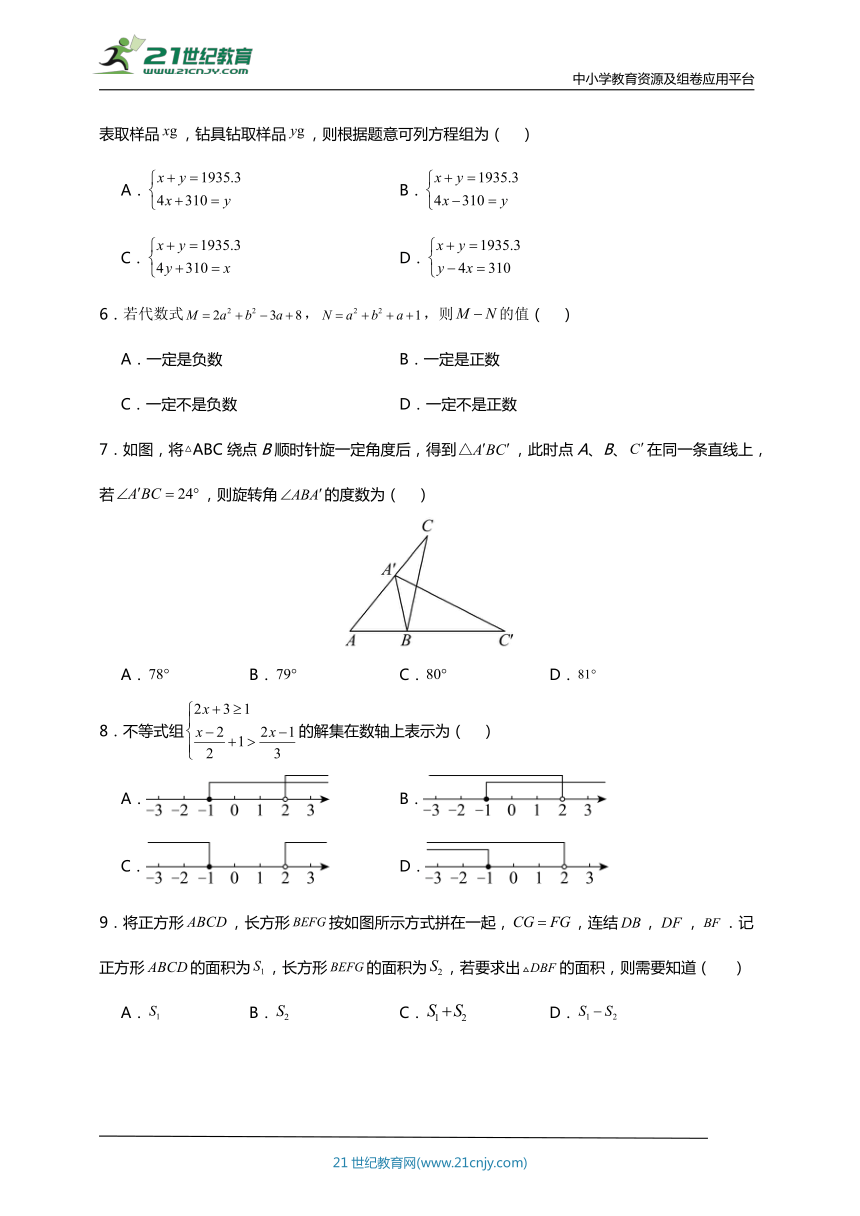
7．如图，将△ABC绕点B顺时针旋一定角度后，得到，此时点A、B、在同一条直线上，若，则旋转角的度数为（ ）
A． B． C． D．
8．不等式组的解集在数轴上表示为（ ）
A． B．
C． D．
9．将正方形，长方形按如图所示方式拼在一起，，连结，，．记正方形的面积为，长方形的面积为，若要求出的面积，则需要知道（ ）
A． B． C． D．
第9题 第10题
10．如图，将四边形折叠，折痕为，连接并延长交延长线于点，若，，平分．则下列结论：①．②；③平分；④．其中错误的有（ ）
A．4个 B．3个 C．2个 D．1个
二、填空题（共8小题，满分24分，每小题3分，请把正确的答案填写在答题卡相应的位置。）
11．已知，则 ．
12．在数轴上到原点的距离小于的点所表示的整数共有 个
13．将一张长方形纸片折叠成如图所示图形，重叠部分是一个三角形，为折痕，若，则的度数为 ．
14．公园里有一块长为，宽为的长方形花坛，现在要把花坛四周均向外扩展，扩展后的长方形花坛的长为，宽为，则扩展后的长方形花坛的面积比扩展前的长方形花坛的面积增加了 ．
15．若不等式组至少有3个整数解，则a的取值范围是 ．
16．如图1是一个长为、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个大正方形，如图2所示，请直接写出之间的等量关系 ．

17．若多项式与的乘积中不含的项，则的值为 ．
18．在“折纸与平行”的拓展课上，老师布置了一个任务：如图，有一张三角形纸片，，，点D是边上的固定点．请在上找一点E，将纸片沿折叠（为折痕），点B落在点F处，使与三角形的一边平行，则的度数为 ．
三、解答题（本大题共9个小题，共76分，解答应写出文字说明、证明过程或演算步骤.）
19．（5分）计算：
20．（8分）（1）已知和都是方程的解，求k与b的值．
（2）解不等式组，并把解集在数轴上表示出来．
21．（6分）先化简，再求值：
其中．
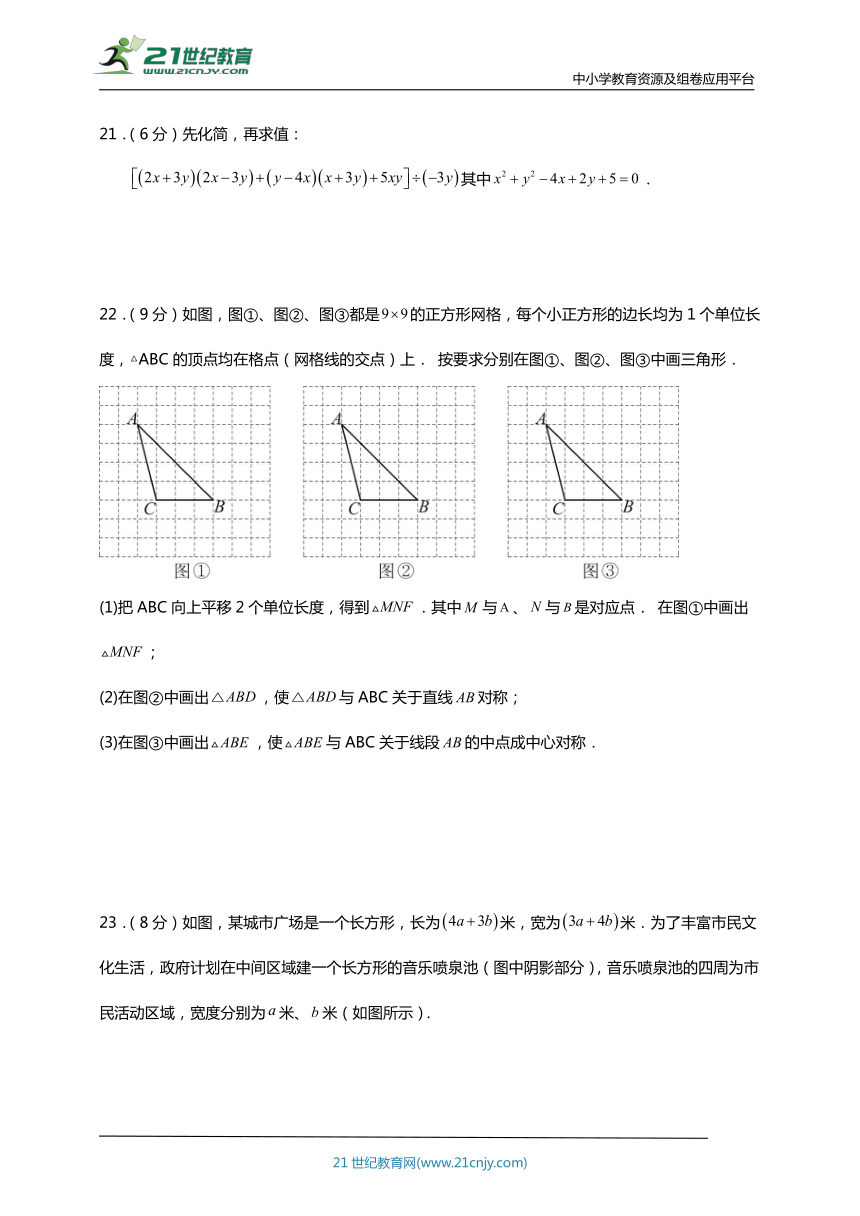
22．（9分）如图，图①、图②、图③都是的正方形网格，每个小正方形的边长均为1个单位长度，△ABC的顶点均在格点（网格线的交点）上． 按要求分别在图①、图②、图③中画三角形．
(1)把ABC向上平移2个单位长度，得到．其中与、与是对应点． 在图①中画出；
(2)在图②中画出，使与ABC关于直线对称；
(3)在图③中画出，使与ABC关于线段的中点成中心对称．
23．（8分）如图，某城市广场是一个长方形，长为米，宽为米．为了丰富市民文化生活，政府计划在中间区域建一个长方形的音乐喷泉池（图中阴影部分），音乐喷泉池的四周为市民活动区域，宽度分别为米、米（如图所示）．
(1)求音乐喷泉池的占地面积（用含，的式子表示）．
(2)若，满足，求该广场音乐喷泉的面积．
(3)在（2）的条件下，音乐喷泉池建成后，需给市民活动区域铺上地砖．若市民活动区域每平米铺设地砖的费用为元，求市民活动区域铺设地砖的费用
24．（8分）“太空育种”是种子被宇航员带入太空，经历一段太空环境后，再返回地球进行培育的育种方法，是将辐射、宇航、育种和遗传等学科综合的高新技术．经太空育种后的鲜花花期更长、花朵更鲜艳、价格也较高.我国培育成功的太空育种鲜花“延丹号”山丹丹单价为元盆，“太空玫瑰”单价为元盆．
(1)为美化环境，公园计划购买这两种太空育种鲜花共盆，若购买这两种鲜花的总价为元，请计算购买“延丹号”山丹丹和“太空玫瑰”的盆数；
(2)若公园购买这两种太空育种鲜花的预算资金只有元，所需购买两种鲜花的总数仍为盆，则最多可购买“太空玫瑰”多少盆？
25．（10分）我们在学习《从面积到乘法公式》时，曾用两种不同的方法计算同一个图的面积，探索了单项式乘多项式的运算法则：（如图1），多项式乘多项式的运算法则：（如图2）以及完全平方公式：（如图3）．
把几个图形拼成一个新的图形，通过图形面积的计算，常常可以得到一些等式，这是研究数学问题的一种常用方法．
(1)观察图4请你写出、、之间的等量关系是_____；
(2)根据（1）中的结论，若，，求出的值；
(3)拓展应用：若，求出的值．
26．（10分）在数学老师的指导下，同学们进行了积极的数学探究性学习活动．
【思考与推理】老师提供了下列一组等式：
第一个等式：；
第二个等式：；
第三个等式：；
第四个等式：；
…
第n个等式可写为：
老师引导同学们将这n个等式相加，做了如下推理：
整理得，
……
…
【类比推广】根据上面等式的特点，同学们类比写出下面一些等式．
第一个等式：；
第二个等式：；
第三个等式：；
第四个等式：；
……
【问题解决】
(1)请你完成【思考与推理】中省略的步骤．
(2)你能写出【类比推广】中的第5个等式：__________________________；猜想第n个等式：___________________，请你证明这个猜想．
(3)你能利用【思考与推理】的思路和成果，直接写出关于的公式．
27．（12分）【问题背景】
同学们，我们一起观察小猪的猪蹄，你会发现一个我们熟悉的几何图形（如图1），我们就把这个图形形象的称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．
（1）如图（1），，为、之间一点，连接、，得到，试探究与，之间的数量关系，并说明理由．
【实际运用】
（2）消防云梯的示意图如图（2）所示，其由救援台、延展臂（在的左侧）、伸展主臂、支撑臂构成，在作业过程中，救援台、车身及地面三者始终保持水平平行．为了参与一项高空救援工作，需要进行作业调整，如图（3）．使得延展臂与支撑臂所在直线互相垂直，且，这时展角______°．
【深入探索】
（3）今年元宵节小美江边观赏灯光秀时，发现两岸灯光在有规律的旋转．如图（4），射线从开始，绕点以10°每秒的速度逆时针旋转，同时射线从开始，绕点以25°每秒的速度逆时针旋转，直线与直线交于，若直线与直线相交所夹的锐角为45°，请求出运动时间秒（）的值．
答案与解析
一．选择题（共10小题，满分30分，每小题3分，每题均有四个选项，其中只有一个选项符合规定,把答案用2B铅笔填涂在答题卡相应的位置.）
1．计算的结果是（ ）
A． B． C． D．
【答案】D
【分析】本题主要考查了积的乘方计算，根据计算求解即可．
【详解】解：，
故选：D．
2．博物馆是历史的见证者和收录者，是人们直观感受历史脉络，提升历史认知的重要场所．以下四个博物馆标识，其文字上方的图案不是轴对称图形的是（ ）
A． B． C． D．
【答案】B
【分析】本题考查轴对称图形识别．如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．根据定义逐项判断即可．
【详解】解：A，文字上方的图案是轴对称图形，不合题意；
B，文字上方的图案不是轴对称图形，符合题意；
C，文字上方的图案是轴对称图形，不合题意；
D，文字上方的图案是轴对称图形，不合题意；
故选B．
3．选：D
4．下列命题为假命题的是（ ）
A．对顶角相等
B．有一条公共边，且互补的两个角互为邻补角
C．两直线平行，内错角相等
D．过直线外一点有且只有一条直线与已知直线平行
【答案】B
【分析】本题考查了对角顶的性质，邻补角的定义，两直线平行内错角相等，平行公理，判断命题的真假，解答关键是熟悉上述知识，并能运用求解．
根据对顶角的性质可判断A；根据邻补角的定义可判断B；根据平行线的性质可判断C；根据平行公理可判断D．
【详解】对顶角相等这是对顶角的性质，它是真命题，故A不符合；
如图，，但它们不是邻补角，所以“有一条公共边，且互补的两个角互为邻补角”是假命题，故B符合；
两直线平行，内错角相等，这是平行线的一条性质，它是真命题，故C不符合；
过直线外一点有且只有一条直线与已知直线平行是真命题，故D不符合．
故选：B．
5．嫦娥六号于2024年6月2日成功着陆在月球背面南极一艾特肯盆地预选着陆区，开启人类探测器首次在月球背面实施的样品采集任务．嫦娥六号采用了机械臂表取和钻具钻取两种方式共采集样品，假设机械臂表取采集的样品数量比钻具钻取采集的样品数量的4倍还多．若设机械臂表取样品，钻具钻取样品，则根据题意可列方程组为（ ）
A． B．
C． D．
【答案】C
【分析】本题主要考查了二元一次方程组的实际应用，设机械臂表取样品，钻具钻取样品，根据两种方式共采集样品，可得方程，根据机械臂表取采集的样品数量比钻具钻取采集的样品数量的4倍还多，可得方程，据此列出方程组即可得到答案．
【详解】解：由题意得，，
故选：C．
6．若代数式，，则的值（ ）
A．一定是负数 B．一定是正数
C．一定不是负数 D．一定不是正数
【答案】B
【分析】本题考查了整式的运算和配方法，做题的关键是配方法的灵活应用．依题意，求解，配方成完全平方公式求解即可．
【详解】解：依题意可得：
，
，
，
的值一定是正数，
故选：B．
7．如图，将△ABC绕点B顺时针旋一定角度后，得到，此时点A、B、在同一条直线上，若，则旋转角的度数为（ ）
A． B． C． D．
【答案】A
【分析】本题主要考查了旋转的性质，熟练地掌握对应点与旋转中心连线的夹角等于旋转角是解题的关键．
根据旋转的性质可知，用减去的度数再除以2即可求出旋转角的度数．
【详解】解：∵绕点B顺时针旋转，得到，
，
，
，
，
故选：A．
8．不等式组的解集在数轴上表示为（ ）
A． B．
C． D．
【答案】B
【分析】本题主要考查了解一元一次不等式组、在数轴上表示不等式组的解集等知识，正确解该不等式组是解题关键．分别解两个不等式，然后根据“同大取大，同小取小，大小小大中间找，大大小小找不到”的原则确定该不等式组的解集，然后将其表示在数轴上即可．
【详解】解：，
解不等式①，可得 ，
解不等式②，可得 ，
∴该不等式的解集为 ，
将其表示在数轴上如图所示：
故选：B．
9．将正方形，长方形按如图所示方式拼在一起，，连结，，．记正方形的面积为，长方形的面积为，若要求出的面积，则需要知道（ ）
A． B． C． D．
【答案】A
【分析】本题考查完全平方公式与几何的综合应用，设，，分割法表示出阴影部分的面积，进行判断即可．
【详解】解：由题意，设，，
则：，，
∴的面积
；
故只需要知道即可求出的面积；
故选A．
10．如图，将四边形折叠，折痕为，连接并延长交延长线于点，若，，平分．则下列结论：①．②；③平分；④．其中错误的有（ ）
A．4个 B．3个 C．2个 D．1个
【答案】D
【分析】本题主要考查了平行线的判定与性质，角平分线的定义，翻折的性质等知识，利用平行线的性质可得，从而得出，即可得出①正确，由平行线的性质和翻折的性质可知②正确；根据平行线的性质可得，若平分，则可证明，根据现有条件无法说明，从而得不到平分，故③错误；设，则，再利用翻折和平行线的性质表示出的度数，从而判断④正确．
【详解】解：，
，
，
，
，故①正确；
，
四边形折叠，
，故②正确；
平分，
，
，
，
若平分，则，
∴，即，
根据现有条件无法说明，即不能说明，故得不到平分，故③错误；
设，
则，
，
，，
，故④正确，
综上所述，错误的有③，
故选：D．
二、填空题（共8小题，满分24分，每小题3分，请把正确的答案填写在答题卡相应的位置。）
11．已知，则 ．
【答案】16
【分析】此题考查了同底数幂的除法运算，正确将原式变形是解题关键．直接利用同底数幂的除法运算法则计算得出答案．
【详解】∵
∴．
故答案为：16．
12．5
13．将一张长方形纸片折叠成如图所示图形，重叠部分是一个三角形，为折痕，若，则的度数为 ．
【答案】
【分析】本题考查了折叠的性质，平行线的性质，平角定义，掌握知识点的应用是解题的关键．
由折叠性质可知，，又，则，设，然后根据平角定义求出的值即可．
【详解】解：由折叠性质可知，，
∵，
∴，
设，
∴，
∵，
∴，解得：，
∴，
故答案为：．
14．公园里有一块长为，宽为的长方形花坛，现在要把花坛四周均向外扩展，扩展后的长方形花坛的长为，宽为，则扩展后的长方形花坛的面积比扩展前的长方形花坛的面积增加了 ．
【答案】/
【分析】本题主要考查了多项式乘法在几何图形中的应用，根据长方形面积计算公式分别求出扩展前后图形的面积，二者相减即可得到答案．
【详解】解：
，
∴扩展后的长方形花坛的面积比扩展前的长方形花坛的面积增加了，
故答案为：．
15．若不等式组至少有3个整数解，则a的取值范围是 ．
【答案】
【分析】本题考查根据一元一次不等式组解集的情况求参数，解题的关键是：熟练掌握一元一次不等式组的整数解, 先求出不等式组的解集，再根据恰有3个整数解，即可求解．
【详解】解：不等式组，得：，
∵至少有3个整数解，3个整数解为：，，
∴，
故答案为：．
16．如图1是一个长为、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个大正方形，如图2所示，请直接写出之间的等量关系 ．

【答案】
【分析】分别求出图2中大正方形，阴影及小长方形的面积，即可得到等式．
【详解】解：图2中大正方形的面积为，阴影图形的面积为，四个小长方形的面积为，
∴，
故答案为：．
17．若多项式与的乘积中不含的项，则的值为 ．
【答案】
【分析】本题主要考查了多项式乘法中的无关型问题，负整数指数幂，根据多项式乘以多项式的计算法则求出的展开结果，再根据结果中不含的项求出，据此代值计算即可得到答案．
【详解】解：
，
∵多项式与的乘积中不含的项，
∴，
∴，
故答案为：．
18．在“折纸与平行”的拓展课上，老师布置了一个任务：如图，有一张三角形纸片，，，点D是边上的固定点．请在上找一点E，将纸片沿折叠（为折痕），点B落在点F处，使与三角形的一边平行，则的度数为 ．
【答案】或或
【分析】本题考查折叠性质、平行线性质，熟练掌握折叠性质，利用分类讨论思想，结合图形进行角的运算是解答的关键．
分，，三种情况，利用折叠性质和平行线的性质求解即可．
【详解】解：当时，如图，则，
由折叠性质得：，
∴，
当时，如图，则，
由折叠性质得：，
∴；
当时，如图，则，
由折叠性质得：，
∴．
综上，的度数为或或．
故答案为：或或．
三、解答题（本大题共8个小题，共76分，解答应写出文字说明、证明过程或演算步骤.）
19． 1
20．（6分）（1）已知和都是方程的解，求k与b的值．
（2）解不等式组，并把解集在数轴上表示出来．
【答案】（1）；（2），在数轴上表示解集见数轴．
【分析】本题考查二元一次方程组，一元一次不等式（组）的解法，解题的关键是掌握不等式组解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
（1）根据方程解的定义构造方程组，利用加减消元法求解可得；
（2）分别解出两个不等式的解集，再根据“大小小大中间找”确定不等式组的解集即可．
【详解】解：（1）把知和代入方程
，
解得 ；
（2）
解不等式，得：，
解不等式，得：，
则不等式组的解集为，
将不等式组的解集表示在数轴上如下：
21．（6分）先化简，再求值：
其中．
【答案】，2
【分析】本题考查整式的混合运算，化简求值，先根据整式的运算法则，乘法公式进行化简，根据，利用非负性求出的值，再代入化简后的整式中进行计算即可．
【详解】解：
；
∵，
∴，
∴，
∴，，
∴，，
∴原式．
22．（8分）如图，图①、图②、图③都是的正方形网格，每个小正方形的边长均为1个单位长度，△ABC的顶点均在格点（网格线的交点）上． 按要求分别在图①、图②、图③中画三角形．
(1)把ABC向上平移2个单位长度，得到．其中与、与是对应点． 在图①中画出；
(2)在图②中画出，使与ABC关于直线对称；
(3)在图③中画出，使与ABC关于线段的中点成中心对称．
【答案】(1)见解析(2)见解析(3)见解析
【分析】此题考查了平移、轴对称、中心对称的作图，读懂题意，准确作图是关键．
（1）按照平移方式找到对应点，顺次连接即可；
（2）按照对称轴找对应点，顺次连接即可；
（3）按照中心对称的定义找到对应点，顺次连接即可．
【详解】（1）解：如图，即为所求；
（2）如图，即为所求，
（3）如图，即为所求，
23．（9分）如图，某城市广场是一个长方形，长为米，宽为米．为了丰富市民文化生活，政府计划在中间区域建一个长方形的音乐喷泉池（图中阴影部分），音乐喷泉池的四周为市民活动区域，宽度分别为米、米（如图所示）．
(1)求音乐喷泉池的占地面积（用含，的式子表示）．
(2)若，满足，求该广场音乐喷泉的面积．
(3)在（2）的条件下，音乐喷泉池建成后，需给市民活动区域铺上地砖．若市民活动区域每平米铺设地砖的费用为元，求市民活动区域铺设地砖的费用
【答案】(1)音乐喷泉池的占地面积为
(2)
(3)市民活动区域铺设地砖的费用为元
【分析】本题主要考查了整式乘法的应用，代数式求值，熟练掌握运算法则是解题的关键．
（1）根据题意列式，再根据多项式乘多项式计算即可；
（2）根据非负数的性质，得出，代入（1）的式子进行计算即可求解；
（2）先根据题意列式求出市民活动区域的面积，再列式计算求出铺设地砖的费用即可，将，代入即可求解．
【详解】（1）解：由题可得音乐喷泉池的占地面积为
．
答：音乐喷泉池的占地面积为．
（2）解：，
∴
解得： ，
∴
（3）解：由题可得市民活动区域的面积为
．
市民活动区域每平米铺设地砖的费用为80元，
．
当时，
答：市民活动区域铺设地砖的费用为元．
24．（8分）“太空育种”是种子被宇航员带入太空，经历一段太空环境后，再返回地球进行培育的育种方法，是将辐射、宇航、育种和遗传等学科综合的高新技术．经太空育种后的鲜花花期更长、花朵更鲜艳、价格也较高.我国培育成功的太空育种鲜花“延丹号”山丹丹单价为元盆，“太空玫瑰”单价为元盆．
(1)为美化环境，公园计划购买这两种太空育种鲜花共盆，若购买这两种鲜花的总价为元，请计算购买“延丹号”山丹丹和“太空玫瑰”的盆数；
(2)若公园购买这两种太空育种鲜花的预算资金只有元，所需购买两种鲜花的总数仍为盆，则最多可购买“太空玫瑰”多少盆？
【答案】(1)购买“延丹号”山丹丹盆，购买“太空玫瑰”盆；
(2)最多可购买“太空玫瑰”盆．
【分析】此题主要考查了二元一次方程组和一元一次不等式的应用，关键是正确理解题意，找出题目中的等量关系和不等关系，列出方程组和不等式．
（）设购买“延丹号”山丹丹盆，购买“太空玫瑰”盆，由题意得， 然后解方程组即可；
（）设购买“太空玫瑰”盆， 由题意得，然后解不等式，再检验即可．
【详解】（1）解：设购买“延丹号”山丹丹盆，购买“太空玫瑰”盆，
由题意，得，
解得，
答：购买“延丹号”山丹丹盆，购买“太空玫瑰”盆；
（2）解：设购买“太空玫瑰”盆，
由题意，得，
解得，
因为为正整数，
所以的最大值为，
答：最多可购买“太空玫瑰”盆．
25．（10分）我们在学习《从面积到乘法公式》时，曾用两种不同的方法计算同一个图的面积，探索了单项式乘多项式的运算法则：（如图1），多项式乘多项式的运算法则：（如图2）以及完全平方公式：（如图3）．
把几个图形拼成一个新的图形，通过图形面积的计算，常常可以得到一些等式，这是研究数学问题的一种常用方法．
(1)观察图4请你写出、、之间的等量关系是_____；
(2)根据（1）中的结论，若，，求出的值；
(3)拓展应用：若，求出的值．
【答案】(1)(2)(3)
【分析】本题考查乘法公式与几何图形的关系，读懂题意，数形结合是解决问题的关键．
（1）如图所示，大正方形的边长为，小正方形的边长为，从而根据大正方形的面积小正方形的面积4个长方形面积，代值求解即可得到答案；
（2）由（1）中得到的关系式，代值求解即可得到答案；
（3）由完全平方和公式，恒等变形后代值求解即可得到答案．
【详解】（1）解：，
，
故答案为：；
（2）解：由（1）可得，，
，
；
（3）解：
，
，
．
26．（10分）在数学老师的指导下，同学们进行了积极的数学探究性学习活动．
【思考与推理】老师提供了下列一组等式：
第一个等式：；
第二个等式：；
第三个等式：；
第四个等式：；
…
第n个等式可写为：
老师引导同学们将这n个等式相加，做了如下推理：
整理得，
……
…
【类比推广】根据上面等式的特点，同学们类比写出下面一些等式．
第一个等式：；
第二个等式：；
第三个等式：；
第四个等式：；
……
【问题解决】
(1)请你完成【思考与推理】中省略的步骤．
(2)你能写出【类比推广】中的第5个等式：__________________________；猜想第n个等式：___________________，请你证明这个猜想．
(3)你能利用【思考与推理】的思路和成果，直接写出关于的公式．
【答案】(1)详见解析
(2)，，证明见解析
(3)，见解析
【分析】本题考查了整式的混合运算，数字类规律探索，熟练掌握各知识点，理解题意是解题的关键．
（1）根据等式的性质以及完全平方公式计算即可；
（2）根据已知的前4个等式总结出第5个等式，以及第n个等式的规律，并将等式左右两边利用多项式乘多项式展开即可证明相等；
（3）先通过，将等式中的从、、、依次取到时，就可得个等式，再累加即可，
【详解】（1）解：剩余步骤为：，
∴，
∴；
（2）解：【类比推广】中的第5个等式：；猜想第n个等式：，
证明：左边，
右边，
∵左边右边，
∴原式成立；
（3）解：，
当式中的从、、、依次取到时，就可得下列个等式：
，
，
，
，
，
将这个等式的左右两边分别相加得：，
即
．
27．（12分）【问题背景】
同学们，我们一起观察小猪的猪蹄，你会发现一个我们熟悉的几何图形（如图1），我们就把这个图形形象的称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．
（1）如图（1），，为、之间一点，连接、，得到，试探究与，之间的数量关系，并说明理由．
【实际运用】
（2）消防云梯的示意图如图（2）所示，其由救援台、延展臂（在的左侧）、伸展主臂、支撑臂构成，在作业过程中，救援台、车身及地面三者始终保持水平平行．为了参与一项高空救援工作，需要进行作业调整，如图（3）．使得延展臂与支撑臂所在直线互相垂直，且，这时展角______°．
【深入探索】
（3）今年元宵节小美江边观赏灯光秀时，发现两岸灯光在有规律的旋转．如图（4），射线从开始，绕点以10°每秒的速度逆时针旋转，同时射线从开始，绕点以25°每秒的速度逆时针旋转，直线与直线交于，若直线与直线相交所夹的锐角为45°，请求出运动时间秒（）的值．
【答案】（1），理由见解析；（2）；（3）3秒或9秒
【分析】本题主要考查了旋转的定义、平行线的性质、三角形外角的性质、垂直的定义等知识点，灵活运用相关性质定理是解题的关键．
（1）如图，过E点作，根据平行线的性质、角的和差以及等量代换即可解答；
（2）如图：延长相交于点P，过P作，易得则、，由垂直的定义可得，然后根据角的和差以及平行线的性质即可解答；
（3）将直线的点M平移与直线的N点重合，然后根据题意分情况画出图形，根据旋转的性质列出关于t的方程求解即可．
【详解】解：（1），理由如下：
如图，过E点作，
∵，
∴，
∴，
∴．
（2）如图：延长相交于点P，过P作，
∵，
∴，
∴，，
∵，
∴，
∴，
∴；
（3）将直线的点M平移与直线的N点重合，
根据题意得，，
∴，
由题意可得：，
∴，解得：；
根据题意得，，
由题意可得：，
∴，
∴，解得：；
根据题意得，，
由题意可得：，
∴，
∴，解得：（不符合题意）；
综上所述，运动时间秒为3或9．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)

展开更多......

收起↑