资源简介

第九章 图形的变化
9.2轴对称
9.2.4 轴对称图形
本节课是苏科版初中数学七年级下册第九章第二节第4课时，具有承上启下的重要作用．从知识体系上看，轴对称图形是是在学生已认识简单平面图形基础上，对图形性质和变换的深入探究，为学习全等三角形、等腰三角形等知识筑牢根基．在生活中，轴对称现象广泛存在，学习这部分内容有助于培养学生用数学眼光观察世界，提升数学应用意识．
教材先从生活中大量轴对称例引入，如北京天坛、脸谱、建筑、剪纸等图案，让学生直观感受轴对称图形，形成初步感性认识．接着给出轴对称图形和对称轴的定义，之后在常见轴对称图形：线段、角，等腰三角形，等边三角形，长方形，正方形，详细阐述它们的轴对称特征．然后讲解角平分线的尺规作图．教材内容由易到难，先呈现具体操作步骤，再深入剖析内在原理，便于学生理解和掌握．
在小学阶段，学生已对简单的轴对称图形有了初步认识，如长方形、正方形、圆形等，能直观辨别一些明显的轴对称现象，知晓对称轴的概念，能找出简单图形的对称轴．然而，这些认识多停留在直观感知层面，对轴对称的本质和内在规律缺乏深入理解．
学生在七上学习中接触过简单尺规作图，像作一条线段等于已知线段、作一个角等于已知角，对尺规的基本使用方法有初步了解．然而，角平分线尺规作图步骤更复杂，原理涉及全等三角形等知识，学生需要将已有作图技能和新知识进行整合．
1.观察并感受生活中的轴对称，归纳轴对称图形的概念，能识别简单的轴对称图形，能找出并画出轴对称图形的所有对称轴,发展空间观念.
2.会用尺规作已知角的角平分线,提高作图的能力.
3.在探究作已知角的平分线的方法中，培养学生的几何直觉；培养学生探究问题的兴趣，增强探究问题的信心；体验数学活动的探索性和创造性.
重点： 掌握轴对称图形的概念，，能识别简单的轴对称图形，能找出并画出轴对称图形的所有对称轴,
难点： 会用尺规作已知角的角平分线,提高作图的能力.
情境导入
师：人们很欣赏物体的对称性，设计师、艺术家常利用对称性使作品美观大方
师生活动：教师带领学生观察图片，吸引学生的注意力，与学生共同感知轴对称现象．
设计意图：通过创设情境，让同学们在实际情境中发现轴对称现象，并激发学生研究实际物体
与数学之间的联系，让学生明白数学来源于生活，又会服务于生活，
探究新知
活动一：轴对称图形的定义
问题：观察下面三个图案，它们有什么共同特征
答：图案沿直线l折叠，直线两旁的部分能够互相重合.
师引导学生总结：
轴对称图形：如果一个图形关于某条直线成轴对称的图形是其本身,那么称这个图形是轴对称图形,这条直线就是对称轴.
师生活动：学生先独立思考，指定学生回答，师最后总结.
设计意图：教师带领学生观察图案，如精美的京剧脸谱、古老的中式建筑、复杂的剪纸艺术，吸引学生的注意力，与学生共同感知轴对称图形．归纳总结出轴对称图形的定义，进一步培养学生归纳总结的能力.
活动二：轴对称图形的对称轴
下列各图是轴对称图形吗 如果是,画出对称轴 .
答：
思考：如何判断一个图形是否为轴对称图形呢？
师小结：要判断一个图形是否为轴对称图形，可以把这个图形沿某一条直线对折,如果对折后的两部分关于这条直线对称，那么原来的图形就是轴对称图形，这条直线是对称轴 .
师生活动：教师请各小组代表发言，说说如何判断的，对学生的回答进行点评，强调判断一个图形是否为轴对称图形的关键要点，并思考轴对称图形与两个图形成轴对称有什么区别与联系？
设计意图：引导学生在观察、操作、讨论中掌握如何判断一个图形是不是轴对称图形，能够找出轴对称图形所有的对称轴，加深对轴对称图形以及对称轴的概念理解，锻炼思维，培养合作交流能力，感受数学与生活的联系.
活动三：轴对称图形与两个图形成轴对称的区别与联系
思考：轴对称图形与两个图形成轴对称有什么区别与联系？
师生活动：教师请各小组代表发言，总结轴对称图形与两个图形成轴对称的区别与联系，对学生的回答进行点评.学生认真聆听其他小组发言，补充自己的想法．
设计意图：通过比较，进一步认识轴对称图形与两个图形成轴对称本质特征，让学生运用辩证的观点认识事物，进一步发展学生抽象思维能力，提升数学综合素养．
应用新知
例1.尺规作图：如图，已知∠AOB，作∠AOB 的平分线.
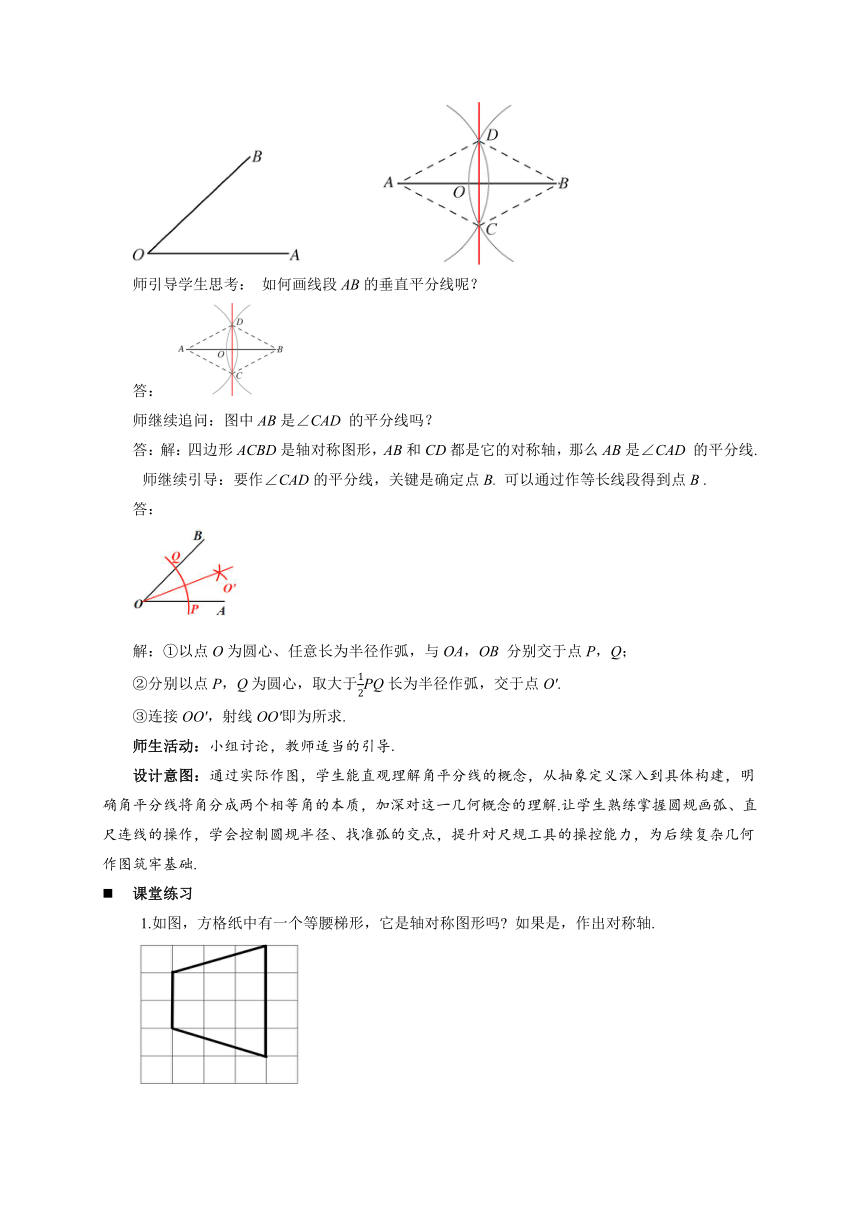
师引导学生思考： 如何画线段AB的垂直平分线呢？
答：
师继续追问：图中AB是∠CAD 的平分线吗？
答：解：四边形ACBD是轴对称图形，AB和CD都是它的对称轴，那么AB是∠CAD 的平分线.
师继续引导：要作∠CAD的平分线，关键是确定点B. 可以通过作等长线段得到点B .
答：
解：①以点O为圆心、任意长为半径作弧，与OA，OB 分别交于点P，Q；
②分别以点P，Q为圆心，取大于PQ长为半径作弧，交于点O'.
③连接OO'，射线OO'即为所求.
师生活动：小组讨论，教师适当的引导.
设计意图：通过实际作图，学生能直观理解角平分线的概念，从抽象定义深入到具体构建，明确角平分线将角分成两个相等角的本质，加深对这一几何概念的理解.让学生熟练掌握圆规画弧、直尺连线的操作，学会控制圆规半径、找准弧的交点，提升对尺规工具的操控能力，为后续复杂几何作图筑牢基础.
课堂练习
1.如图，方格纸中有一个等腰梯形，它是轴对称图形吗 如果是，作出对称轴.
答：解：它是轴对称图形，对称轴如图所示.
2.如图，方格纸上有两条线段，请用不同的方法将其补成一个轴对称图形.
答：
师小结：在网格中画轴对称图形的方法和步骤.
补成一个轴对称图形，首先是确定 ，然后是找出 .（对称轴 对应点）
请把如图，光线射向水平镜面，反射角等于入射角. 入射光线与反射光线是否成轴对称 如果是，作出对称轴.
答：解：入射光线与反射光线成轴对称，作出的对称轴如图所示..
师总结：1.反射角等于入射角；
2.等角的余角相等.
限时训练
1．中国体育代表团在2024年巴黎奥运会取得优异成绩．下列图标是奥运会上常见的运动图标，其中是轴对称图形的是（ ）
A． B．
C． D．
答：B
2.指出下列图形各有几条对称轴，画出每个图形的对称轴.
答：
3.已知：如图，点都在方格纸的格点上，请找出符合条件的格点D，使图中的4点组成一个轴对称图形.
解：如图所示：D1，D2，D3，D4都是符合条件的点．
4.如图，将一张三角形纸片的一角折叠，使点A落在△ABC外的处，折痕为DE．
如果，，，那么下列式子中正确的是（ ）
A． B．
C． D．
答案：解：设A'D与CE交于点F，如图..
由折叠可得∠A=∠A'=α.
因为∠BDA'是 △ADF的外角，∠AFD是 △A'EF的外角，
所以∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，
所以∠BDA'=θ =α+α+β =2α+β .故选：．
5.如图，在△ABC中，AD⊥BC，∠B=30°，∠C=52°．
(1)实践与操作：用尺规作图法作∠BAC的平分线AE交BC于点E；(保留作图痕迹，不要求写作法)；
(2)应用与计算：在(1)的条件下，求∠DAE的度数．
答：（1）解：如图所示.
（2）解：因为∠B =30°，∠C =52°，
所以∠BAC=180°- ∠B- ∠C =98°，
因为AE平分∠BAC ，所以∠BAC=2∠CAE，所以∠CAE=49°，
因为AD⊥BC，所以∠ADC=90°，
所以∠CAD=180°- ∠ADC-∠C =38°，
所以∠DAE=∠CAE-∠CAD=11°.
师生活动：学生独立思考，然后指定学生回答，教师给予适当的评价
设计意图：通过课堂练习巩固新知，加深对本节课的理解及应用.
归纳总结
设计意图：通过归纳总结让学生进一步熟悉巩固本节课所学的知识.
本课通过引入生活实例，让学生直观感受轴对称图形的美与特点，激发了他们的学习兴趣，学生在观察、折叠图形的实践活动中，自主探索出轴对称图形的定义和性质，培养了动手能力和空间观念.小组合作环节，学生积极讨论，分享不同的想法，课堂氛围活跃，合作学习效果良好.
在尺规作图的操作环节，让学生先自主尝试，再观看示范，最后反复练习.学生逐步掌握了作图的方法，对几何图形的理解也更加深刻，动手能力得到了锻炼.
但在逻辑推理素养培养上稍显不足，后续教学会增设推理训练，引导学生有条理阐述，强化逻辑思维.

展开更多......

收起↑